El aprendizaje activo de la física (aaf) está formado por un conjunto de métodos bien definidos y pensados para mejorar el aprendizaje de la física (Mora, 2008). Esta concepción coincide con las descripciones de Thornton y Sokoloff (1998), los cuales consideran al aaf como una estrategia didáctica en donde los estudiantes son guiados a construir su conocimiento de los conceptos físicos mediante observaciones directas del mundo físico. Se requiere que los estudiantes efectúen predicciones, observaciones, discusiones y síntesis, lo cual constituye el ciclo pods (Sokoloff et al., 2006), a fin de que actúen y reporten sus propios enfoques y resoluciones a las situaciones que se les presentan. Todo esto puede realizarse con base en lo observado en las gráficas obtenidas en tiempo real o en el análisis de simulaciones por computadora o en la solución de problemas interactivos, entre otras opciones. El ciclo pods tiene su antecedente en otra secuencia de enseñanza de las ciencias propuesto por White y Gunstone (1992), esto es, predecir, observar y explicar (poe). A continuación, detallaremos más la estrategia de enseñanza del ciclo pods.

– Predicción. El profesor debe empezar proponiendo preguntas a los estudiantes, para que ellos intenten hallar la respuesta correcta. El aaf considera los conocimientos previos del estudiante alrededor de los fenómenos de la física, y ayuda a pensar con mayor profundidad en los fenómenos físicos.

– Observación. En esta acción los estudiantes reproducen y observan los fenómenos en estudio y logran aprender haciendo (Vázquez y Rúa, 2007), lo cual no es nada nuevo; es como siempre se ha aprendido, como se sigue aprendiendo, “pues lo que hay que hacer después de haber aprendido, lo aprendemos haciéndolo” (Aristóteles, 2015).

– Discusión. Posteriormente discuten los fenómenos observados en clase con sus pares en pequeños grupos de tres a cuatro participantes como máximo. La discusión sobre el material de enseñanza permite mejorar la comprensión de conceptos, apoya la autorregulación de tal forma que los estudiantes escuchan diferentes ideas, reflejan las propias y éstas les ayudan para abordar errores conceptuales. Mediante la discusión, los estudiantes pueden también llegar a familiarizarse con el lenguaje científico (Lemke, 1990). Asimismo, se promueve la discusión mediante el uso de lluvia de ideas, la utilización de mapas conceptuales, de las tecnologías de la información y de la comunicación (tic), entre otras características.

– Síntesis. Esta última parte del ciclo es sumamente importante para la correcta formación de conceptos físicos, pues los estudiantes reportan sus propios enfoques y resoluciones a las situaciones que se les presentan (Vázquez y Rúa, 2007). Los estudiantes aprenden equivocándose y reflexionando sobre cómo resolver los problemas, de preferencia con la ayuda de alguien más experimentado, realizando conexiones e incluso equivocándose, pues no hay aprendizaje sin error (Cazau, 2007).

En el aaf el estudiante se ve implicado activamente y asume el control de su propio aprendizaje, se provoca que el estudiante pueda analizar, investigar, colaborar, compartir, construir y generar conocimiento basándose en sus conocimientos previos y en su iniciativa propia. Los efectos y características tangibles de este aprendizaje en el estudiante son que:

– Los estudiantes desarrollan un mejor entendimiento conceptual de los principios de la física. Los estudiantes obtienen mayor ganancia conceptual debido al uso de las herramientas diseñadas para tal efecto al aplicar las estrategias de aprendizaje basadas en los resultados de las evaluaciones aplicadas antes de la instrucción. Se utilizan las características de aprendizaje (kinestésico, auditivo o visual), capacidad mental y organización de la memoria; la ganancia obtenida en el aprendizaje activo es mayor que los resultados reportados para la instrucción por conferencia y la retención de conocimientos es duradera (Felder et al., 1998).

– Los estudiantes desarrollan mejores capacidades para la solución de problemas. Los estudiantes que trabajan con el método de aprendizaje activo solucionan los problemas con más facilidad que los sometidos al tipo de conferencia magistral. Inversamente, los problemas de evaluación final usados en la clase basada en conferencia magistral son a menudo demasiado fáciles para incluirlos en el examen final para la clase con aprendizaje activo. Los estudiantes aprenden haciendo (Sokoloff et al., 2007).

– Los estudiantes aprenden de ellos, de sus compañeros y del profesor. Desarrollan un mejor entrenamiento y comunicación social. Los estudiantes en un ambiente activo muestran un gran avance desde el principio hasta el fin del curso en su habilidad para explicar a detalle la solución de un problema. Al final del ciclo escolar los estudiantes mejoran su trabajo en grupo. El aprendizaje es fácil, profundo y duradero.

– Los estudiantes se entusiasman más con el curso. Los comentarios de los estudiantes sobre las evaluaciones posteriores a la instrucción indican que prefieren este tipo de instrucción a la conferencia magistral (Bonwell y Eison, 1991).

– Promueve la discusión en grupo. Mediante la tormenta o lluvia de ideas, la utilización de mapas conceptuales, de las tic y otros. Los objetivos de los grupos de discusión son: nivelar, jerarquizar e integrar los conocimientos básicos, trabajar los temas a través de actividades prácticas, motivar a los estudiantes a estudiar con libros de texto y consultar otras fuentes, promover la búsqueda y uso de fuentes de información, fomentar la curiosidad, alentar al estudiante a exponer y defender sus ideas en público en forma clara y correcta, mejorar la expresión escrita y adoptar el lenguaje de expresión científica.

– El proceso de enseñanza es placentero. Esta característica incrementa el entendimiento conceptual del estudiante y la habilidad para resolver problemas, permitiendo disfrutar el curso.

– Provoca la transferencia a situaciones y soluciones semejantes. El entendimiento conceptual permite que los alumnos apliquen los conceptos a situaciones parecidas.

Los resultados de investigación educativa en la física presentados en los últimos años (Stathopoulou & Vosniadou 2007) muestran la necesidad de efectuar cambios en la metodología de enseñanza (Bransford et al., 2000) a fin de incrementar la calidad del aprendizaje al aprovechar las características diferentes de los estudiantes dentro de un contexto de la vida real, con materiales de bajo costo, basándose en el aaf, en un esfuerzo por motivar a los estudiantes a aplicar los principios aprendidos para la solución de problemas de la vida cotidiana y profesional.

2.2 Componentes de las clases
demostrativas interactivas

En los métodos activos se debe tener un facilitador para grupos pequeños (dos a cuatro estudiantes como máximo), con la finalidad de que el aprovechamiento se incremente, también se capacita a los participantes de la metodología de aaf. La actividad se monitorea con diagnósticos estandarizados que permitan evaluar la efectividad de la implementación mediante exámenes pre- test y postest diseñados para el efecto con anticipación. De acuerdo con las concepciones actuales el docente actúa como facilitador y guía entre el conocimiento y los estudiantes, logrando un proceso de interacción basado en la iniciativa y el afán de saber de los alumnos; haciendo del proceso un ciclo e individualizando la instrucción. La formación de grupos de discusión permite la mezcla de estudiantes con diferentes habilidades, y los grupos pueden cambiarse periódicamente.

A continuación, se mostrará la secuencia de aplicación de una clase demostrativa interactiva (Sokoloff 1997; 2004):

1. El instructor describe la demostración y la hace para la clase, sin exhibir los resultados.

2. El facilitador pide a los estudiantes realizar y registrar sus predicciones de forma personal en una “Hoja de la Predicción Individual” diseñada para tal efecto sobre los datos esperados (serie de preguntas sobre la demostración), las hojas se recogen, pero no se califican. Se espera que los estudiantes construyan las respuestas por sí mismos con discusiones entre sus pares y con la supervisión de los facilitadores. Los facilitadores no dan una conferencia; más bien hacen preguntas diseñadas para ayudar a los estudiantes a encontrar sus propias respuestas.

3. Los estudiantes discuten sus predicciones en pequeños grupos (de dos a cuatro como máximo) para llegar a una conclusión final.

4. El facilitador solicita las respuestas dadas por los equipos de trabajo y pide que se registren en la “Hoja de Predicción por Equipos”.

5. El facilitador expone los resultados más comunes centrándose en las ideas previas más importantes y representativas y las muestra en una pantalla o en el pizarrón.

6. Se realiza la experimentación, se registran los datos obtenidos en tiempo real por medio de la computadora o de acuerdo al diseño de la práctica, se muestran los resultados para que todos los vean (por medio de un proyector o en el pizarrón).

7. El instructor pide que los estudiantes describan sus resultados y los discutan, considerando sus predicciones, y deben llegar a una conclusión final.

8. El facilitador discute junto con sus estudiantes la aplicación a situaciones físicas semejantes, basándose en los mismos conceptos.

Esta secuencia se sigue para cada actividad de aprendizaje, los estudiantes pueden realizar sus predicciones de forma individual y/o colectiva entre pares y con el facilitador, observan la demostración, reflexionan sobre lo visto y confirman o rechazan sus predicciones iniciales.

2.3 Cómo impartir clases
demostrativas interactivas efectivas

A continuación, se hacen las siguientes recomendaciones para la efectiva aplicación de las clases demostrativas interactivas:

• El facilitador debe observar cuidadosamente y elegir el momento adecuado para pasar al siguiente paso, debe calcular cuándo ha transcurrido el tiempo suficiente para la discusión (pasos 2, 3 y 4) y continuar con la clase en el tiempo apropiado.

• En el paso 5 el instructor puede utilizar el proyector o el pizarrón para anotar las predicciones de los estudiantes. Las predicciones incorrectas no se corrigen en esta ocasión. El facilitador puede incluir respuestas de demostraciones anteriores si ningún estudiante se ofrece voluntariamente o si las respuestas no varían.

• El propósito de los pasos 7 y 8 es que el instructor dirija a los estudiantes a la respuesta correcta. Esto no es una conferencia (clase tradicional), sino una discusión dirigida donde los datos experimentales (gráficos y/o datos) se utilizan para validar los conceptos.

El estudiante se involucra en su propio proceso de aprendizaje; lo cual, se traduce en mejor retención de lo aprendido; conoce el pensamiento entre pares, respecto al tema que se está aprendiendo, teniendo otras perspectivas o puntos de vista. Aprende a defender sus ideas con argumentos claros desarrollando su capacidad argumentativa y comunicativa. Desarrolla habilidades sociales (integración, respeto, tolerancia, comunicación, etc.) Aprende a reconocer cuándo y cuánta información necesita y se encuentra preparado para transferir lo que se ha aprendido a problemas y escenarios nuevos. No vale apoyarse en los otros. Le permite aprender a aprender para aprender a hacer y llegar a ser.

El facilitador debe elaborar materiales y secuencias de aprendizaje basados en la investigación educativa realizada (indagación de las ideas previas) con la finalidad de que el alumno construya su aprendizaje mediante la aplicación de los mismos. Facilita el aprendizaje y crea situaciones de aprendizaje de las que el educando no puede escapar sin haber aprendido. Fomenta la cooperación entre grupos de trabajo de forma positiva. Dentro de las actividades del facilitador está el prestar atención a cada equipo de trabajo y a cada estudiante de forma personal con la intención de resolver los problemas que puedan surgir. Es importante proporcionar reconocimiento y oportunidad de comprobar su propio progreso a todos los estudiantes.

Una clase demostrativa interactiva se aplica en apenas varias clases de cada semestre; sin embargo —de acuerdo con otros investigadores (Sokoloff, 1997)—, su uso es suficiente para producir beneficios sustanciales. Para cada demostración se tiene una hoja de predicción para los estudiantes, ésta puede incluir gráficos en donde éstos pueden elaborar sus predicciones de forma breve para describir lo observado, así como una serie de preguntas conceptuales.

Se puede utilizar este material para adaptarlo a las características y circunstancias de cada facilitador y de sus alumnos. Para aplicar esta demostración se formaron subgrupos de trabajo de tres a cuatro personas, se aplica la misma en aproximadamente una hora y 40 minutos con la finalidad de mejorar el aprendizaje, de obtener las gráficas de movimiento y para facilitar la elaboración del modelado matemático del fenómeno en estudio. Posteriormente, se aplica algún cuestionario de evaluación conceptual como post test para evaluar la ganancia del aprendizaje o cualquier otro análisis estadístico.

2.4 Evaluación de las clases
demostrativas interactivas

2.4.1 Factor de Hake

Para lograr una medición de la ganancia conceptual primero se debe tener una medida estandarizada del entendimiento conceptual de los estudiantes alrededor del material educativo evaluando los resultados de exámenes resueltos antes y después de la instrucción, de preferencia un test debidamente validado; más adelante se valoran los resultados con la ganancia normalizada (Hake, 1998), la cual permite medir y comparar la ganancia conceptual desarrollada entre en cursos de una misma índole; o bien, comparar entre cursos desarrollados con enseñanza tradicional y los métodos de enseñanza interactivos usados en las escuelas. Los resultados de las dos evaluaciones (pre- y postest) se reportan como un número llamado ganancia normalizada que es la razón del aumento entre el pretest aplicado al inicio del curso y el postest aplicado al final del mismo, con respecto al máximo aumento posible, tiene valores que cubren el intervalo de [0, 1] (Seyed, 2013). De acuerdo a los resultados obtenidos se podrá concluir si efectivamente los documentos construidos con su metodología de trabajo, las herramientas llevadas al aula y su metodología fueron efectivas y cumplieron los objetivos trazados, la expresión matemática es (Hake, 1998):

.(2.1a)

La ganancia del aprendizaje se divide en tres categorías:

• Zona de ganancia alta si el factor de Hake cumple con g ≥ 0.7,

• Zona de ganancia media si el factor de Hake cumple con
0.3 ≤ g < 0.7,

• Zona de ganancia baja si el factor de Hake cumple con g < 0.3.

Para comprender cómo aprenden los estudiantes (Becerra, 2018, pp. 80-91) primero es necesario analizar cómo funciona la memoria y cómo se procesa y almacena la información en el cerebro; según Redish (2003) esta memoria se compone de la memoria a corto y largo plazo, las cuales son complementarias en el sentido de que para acceder a la memoria de largo plazo es necesario activarla por medio de la memoria a corto plazo, la cual trabaja de manera rápida, pero tiene limitaciones, ya que sólo puede manejar grupos pequeños de paquetes de información y desaparece rápidamente, mientras que la memoria a largo plazo es capaz de manejar grandes grupos de paquetes de información, hechos o datos, entre otros, pudiendo permanecer durante periodos largos de tiempo, incluso décadas, al ser esta información productiva y asociativa en un proceso que puede ser en cadena, ya que la activación de un elemento conlleva a la activación de otro.

El hecho de que la memoria a corto plazo sea necesaria para conducir a la memoria a largo plazo orienta el desarrollo de las actividades propuestas en la investigación, ya que permite evitar el exceso de información otorgada a los estudiantes en una sesión de clases; a esta memoria se le adjudica la capacidad para resolver problemáticas, analizar información y almacenarla en nuestra conciencia, siendo ésta individualizada para cada persona, pues depende de su conocimiento y de sus estados mentales, lo que conlleva a afirmar que cuando se puede aplicar de manera fácil un pequeño conocimiento, experiencia o proceso éste está compilado (ejecutado).

Por otro lado, la memoria a largo plazo es cognitiva-experiencial al ser productiva en el contexto de ser activa extrayendo y procesando la información consolidada en la memoria a corto plazo mediante un proceso automático, además, esta memoria no sólo depende del estado mental (correspondiente al modelo físico) cuando se presenta el estímulo, sino también del contexto, pues es la respuesta cognitiva a estímulos mentales al depender de la situación externa que la propicia y de la manera en la cual se da ¿la respuesta o el estímulo?. Esta memoria también se caracteriza por ser estructurada y asociativa, ya que cuando el sujeto se ve expuesto a un estímulo, una sucesión de elementos de conocimiento se puede activar; estas características de la memoria permiten orientar más la propuesta al procurar la creación de ambientes de trabajo que propicien la activación de conocimientos por parte de los estudiantes, lo cual dependerá de los estímulos que se provoquen en el aula en la propuesta realizada, resaltando la importancia de la aplicación del pretest al dar cuenta de las ideas y concepciones previas de los estudiantes, para luego comprender cómo se da el razonamiento en ellos y comprender así los patrones de asociación estímulo-consolidación de conocimiento; haciendo referencia a la estructura de conocimiento generado, estos patrones tienen la posibilidad de activarse no sólo en contextos particulares y propios, sino en una variedad de ellos generando un esquema, el cual, cuando es robusto y coherente, se define como modelo mental; en esta misma línea se habla de modelos científicos como modelos mentales, que se caracterizan por ser constituidos alrededor de las experiencias, propiedades e interacción con fenómenos y objetos, consolidando de esta manera la definición de modelo físico.

2.4.2 Ganancia de Hake-Dellwo

Hovland et al. (1949) utilizaron la relación

Demostración 1: Realiza cinco mediciones y registra los datos.

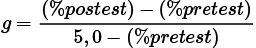.(2.1b)

para cuantificar la efectividad de las películas instructivas. Hake (1998) utilizó (2.1b) para medir la efectividad relativa de varias técnicas de instrucción empleadas en cursos de introducción a la física. Cummings et al. (1999) utilizó (2.1b) para evaluar las innovaciones en la física de estudio. Meltzer (2002) utilizó (2.1b) para explorar la relación entre preparación matemática y aprendizaje de conceptos en física. Estos importantes estudios se basaron en la noción intuitiva de que al comparar dos cursos “El curso con el mayor valor de cambio normalizado (g) es el curso más eficaz”.

Desafortunadamente, como demostró Dellwo (2010), esta regla de evaluación clásica puede llevar a conclusiones contrarias a la intuición. David R. Dellwo (2010) empleó una regla de evaluación alternativa obtenida al descomponer el cambio normalizado (2.1b) en medidas componentes:

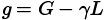.(2.2)

Aquí G es una ganancia normalizada (a la que nos referiremos como Dgain o ganancia de Dellwo) que mide la probabilidad de que un error en el pre test previo a la instrucción del grupo se corrija en el post test después de la instrucción. De manera similar, L es una pérdida normalizada (a la que nos referiremos como Dloss o pérdida de Dellwo) que mide la probabilidad de que una respuesta correcta en la prueba previa a la instrucción del grupo resulte incorrecta en la prueba posterior a la instrucción. El parámetro no negativo γ es un factor de renormalización que depende del desempeño previo a la instrucción de la población. En consecuencia, (2.2) expresa el cambio normalizado (2.1b) como la diferencia entre dos índices no negativos, ganancia normalizada y pérdida renormalizada. La descomposición (2.2) da lugar a una regla de evaluación alternativa que evita las conclusiones contradictorias asociadas con el último resultado, y dice, en parte: “El curso con mayor valor de ganancia normalizada (G) y menor valor de pérdida renormalizada (γL) es el curso más efectivo”.

El cambio normalizado (2.1b) para un grupo de N estudiantes que realizan una prueba de diagnóstico con M preguntas se puede expresar de la siguiente forma:

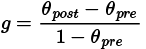,(2.3a)

,(2.3b)

.(2.3c)

La derivación de (2.2) está basada en la siguiente observación.

Esta observación junto con las definiciones (2.3b) y (2.3c) implican que

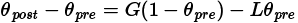.(2.4a)

,(2.5a)

.(2.5b)

El numerador en (2.5a) es el número de preguntas en las que los estudiantes demuestran una ganancia en conocimiento y el denominador es la ganancia máxima posible. En consecuencia, la relación G es una ganancia normalizada que mide la probabilidad condicional (Ross, 2004) de que un error en la prueba previa a la instrucción del grupo se corrija en la prueba posterior a la instrucción. De manera similar, el numerador en (2.5b) es el número de preguntas en las que los estudiantes demuestran una pérdida de conocimiento y el denominador es la máxima pérdida posible. En consecuencia, la razón L es una pérdida normalizada que mide la probabilidad condicional de que una respuesta correcta en la prueba previa a la instrucción del grupo resulte incorrecta en la prueba posterior a la instrucción.

En resumen, la ecuación (2.4a) expresa el cambio en la puntuación de la prueba como una diferencia entre la fracción de preguntas en las que los estudiantes demuestran una ganancia en conocimiento y la fracción en la que demuestran una pérdida de conocimiento. Finalmente, para obtener (2.2) definimos a γ como la siguiente expresión

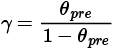,(2.5c)

y dividimos (2.4a) entre (1 − θpre). El factor de escala (2.5c) es un parámetro no negativo cuyo valor es mayor que 1 si θpre > ½, igual a 1 si θpre = ½, y menor que 1 si θ < ½. La escala γ se conoce como la relación de aspecto del grupo y especifica las probabilidades de que el grupo dé una respuesta correcta en la prueba previa a la instrucción.

i. A es más efectiva que B si 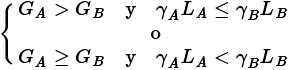,(2.6a)

ii. A y B son igualmente efectivos si 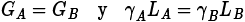,(2.6b)

iii. A y B no son comparables si 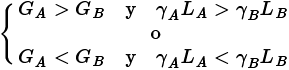.(2.6c)

Obsérvese que, (2.6a) reformula “El curso con el valor mayor de ganancia normalizada (G) y el menor valor de pérdida renormalizada (γL) es el curso más efectivo” en forma algebraica y define un orden consistente de cursos en el sentido de que si A es más efectivo que B y B es más efectivo que C, entonces A es más efectivo que C. Además, (2.6c) ofrece una opción de evaluación no ofrecida por “El curso con el valor mayor de cambio normalizado (g) es el curso más eficaz”, algunos cursos no son comparables.

Si A es un curso más efectivo que B en el sentido de (2.6a), entonces GA − GB es una medida de valor agregado de efectividad mejorada debido a mayores ganancias (Suskie, 2004). Además, γ es una medida de valor agregado de eficacia mejorada debido a las pérdidas renormalizadas más pequeñas que experimentan los estudiantes en el curso más efectivo. Por consiguiente,

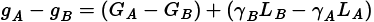,(2.7a)

es una medida de valor agregado de la mejora total en la efectividad cuando se aplica (2.6a) o equivalentemente “El curso con el valor más grande de ganancia normalizada (G) y el valor más pequeño de pérdida renormalizada (γL) es el curso más efectivo” y un curso puede reclamar tanto las mayores ganancias como las menores pérdidas renormalizadas.

Por otro lado, (2.7a) no es una medida de mejora total en la efectividad cuando se aplica (2.6c) y ninguno de los cursos puede reclamar tanto ganancias mayores como pérdidas renormalizadas menores. En este caso, uno de GA − GB y γBLB − γALA es positivo mientras que el otro es negativo; entonces (2.7a) es la diferencia entre dos medidas de valor agregado:

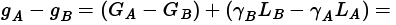
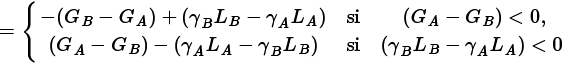.(2.8a)

Es decir, gA − gB es una diferencia entre la eficacia añadida debido a ganancias mayores en un curso y la eficacia añadida debido a pérdidas renormalizadas más pequeñas en el otro curso.

Finalmente, en el esquema de (2.8a) la regla de evaluación clásica: “El curso con el valor mayor de cambio normalizado (g) es el curso más efectivo” declara que A es más efectivo que B cuando se aplica cualquiera de los siguientes:

• La efectividad agregada debido a pérdidas renormalizadas más pequeñas en A compensa la efectividad agregada debido a ganancias más grandes en B.

• La eficacia añadida debida a mayores ganancias en A compensa la eficacia añadida debida a pérdidas renormalizadas más pequeñas en B.

2.4.3 Medidas del modelo mental

Como tal no es posible establecer estrategias para medir los modelos mentales de los estudiantes, pero sí es posible hacer unas observaciones de comportamientos y hacer inferencias sobre éstos, por ejemplo, acerca de los modelos mentales científicamente incorrectos Greca & Moreira (1998) comentan que los estudiantes los construyen de forma natural con su interacción con el mundo al dar una explicación del mismo:

[…] éstos son creados por la percepción, por el ambiente social o por el contexto escolar. Parte de la fuerte resistencia al cambio de esos modelos puede resultar porque son eficientes para entender el mundo antes de entrar en la escuela, y lo continúan siendo fuera de las aulas de ciencia […].

Los modelos mentales de los estudiantes se pueden estudiar analizando sus respuestas al ponerlas en contextos físicos ante la resolución de problemáticas. La importancia de comprender las ideas, razonamientos y relaciones que los estudiantes tienen de los fenómenos físicos es:

1. Visualizar y prever los errores que comúnmente cometen, dando enfoques y aplicaciones erradas a la información abordada en el aula, siendo está información proporcionada por el docente o los libros de texto.

2. Tener en cuenta los recursos que tienen y que son útiles para construir sus futuros conocimientos, siendo estos: la modificación, reestructuración o financiamiento de los esquemas existentes, que se convierten en el material de trabajo para ayudar a mejorar sus modelos y a acercarlos lo más cerca posible a los científicamente aceptados (modelo físico).

Ya se han mencionado los modelos mentales y su relación con los modelos físicos, siendo éstos estructuras mentales robustas y productivas en referencia a la generación de explicaciones de los fenómenos físicos, es allí donde para Sandoval (2009) surge el término dominio conceptual que “Se utiliza a menudo para referirse a ciertos temas específicos de física que involucran a cierto dominio de contextos y reglas explicativas”; un ejemplo de un correcto dominio conceptual es darse cuenta de que entre dos cargas eléctricas la fuerza de atracción o repulsión es directamente proporcional a su carga, e inversamente proporcional al cuadrado de la distancia que las separa, los modelos escolares se caracterizan por:

1. Ser estructuras mentales productivas que pueden aplicarse a los contextos físicos específicos con el fin de obtener unos resultados puntuales.

2. Se asocian con uno y solamente un dominio conceptual físico, aclarando que varios dominios conceptuales pueden tener diferentes conjuntos de modelos.

3. Si se aplica a diferentes casos físicos contextuales relacionados con el mismo dominio conceptual, un modelo es una estructura conceptual estable, lo que conlleva que un modelo es variante ante diferentes contextos relacionados con el mismo dominio conceptual de la física.

2.4.4 Factor de concentración

El factor de concentración sirve como modelo estadístico cuantitativo que permite determinar la “concentración análisis” que da cuenta de la distribución en las respuestas de un examen de selección múltiple, esto con el objetivo de encontrar los perfiles de los modelos conceptuales de los estudiantes. Sandoval (2009) comenta que en un examen de selección múltiple las respuestas obtenidas se pueden relacionar con la aplicación de uno de sus modelos conceptuales dentro de varios contextos físicos, así mismo, comenta que entre otras cuestiones si los estudiantes tienen algún modelo físico consistente las respuestas deben tender hacía una concentración (repetición) hacia una de las opciones del test y, por ende, representará al modelo en cuestión, también recalca que si los estudiantes no tienen ningún modelo, o tienen una variedad de, sus respuestas estarán distribuidas de maneras diferentes entre todas las opciones de respuesta del test. Bao & Redish (2001) plantean un ejemplo en el que se supone un examen de selección múltiple con única respuesta que cuenta con cinco opciones (de la A a la E), si este examen se aplica a 100 estudiantes es posible encontrar distintas opciones en la distribución de las respuestas mostradas a continuación:

Tabla 2.1. Opciones en la distribución de respuestas para una pregunta
Tipo de distribución de respuestas para una pregunta del examen de selección múltiple	Opción de respuesta A	Opción de respuesta B	Opción de respuesta C	Opción de respuesta D	Opción de respuesta E
I	20	20	20	20	20
II	50	10	30	5	5
III	100	0	0	0	0

En la tabla 2.1, el primer caso (I) representa un caso en el que las respuestas a la pregunta se distribuyen de manera equitativa en las cinco opciones de respuesta, de tal manera que se puede asumir que las respuestas fueron diligenciadas al azar, el segundo tipo (II) es un caso común con las realidades educativas en las que las respuestas son más comunes en una opción de respuesta (no necesariamente debe ser la correcta) y las otras opciones tienen también ciertas cantidades, por último, el tipo tres (III) es un caso extremo en el que todos los estudiantes marcan una opción de respuesta (no necesariamente debe ser la correcta) mostrando así 100% en la concentración en una sola opción. Definiendo así al tipo I como el de menor concentración y al tipo III como el de mayor concentración posible.

Al factor que permite determinar la medida de dicha distribución en las respuestas se define como el Factor de concentración, que es un factor normalizado cuyos valores pueden estar entre [0, 1], donde 0 representa un factor de concentración extremadamente bajo y 1 representa el máximo valor de posibilidad en una respuesta de mayor concentración, sin embargo, si el valor es de 0.5 implica una buena concentración debido a que la correspondencia es que alrededor de 60% de los estudiantes seleccionaron una misma opción de respuesta, pero si el valor del factor de concentración oscila entre los 0.2 y 0.5 se relaciona con una situación en la que los estudiantes tienden a dos opciones de respuesta y, finalmente, un valor del factor menor a 0.2 indica una distribución concentrada entre tres o más opciones de respuesta.

Los fundamentos matemáticos para determinar el factor de concentración nacen de definir que en un examen de opción múltiple con única respuesta se tienen varias opciones de respuesta que serán representadas por una variable m con un total N de estudiantes que respondieron la prueba. La respuesta a una de las preguntas puede representarse mediante un vector con m dimensiones (m-dimensional) definido como (k = 1, … , N) representa a los N estudiantes, si la opción escogida fue la correspondiente a la k-ésima opción y en caso contrario. Entonces es posible sumar todas las respuestas de todos los estudiantes para una pregunta dada con este vector de la siguiente forma:

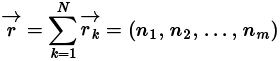.(2.2)

Donde representa la cantidad de estudiantes que escogieron la opción i, lo que de entrada permite analizar que la magnitud del vector indica información sobre la concentración, por ejemplo un valor de magnitud indica una concentración máxima correspondiente al tipo III comentada en la tabla 2.1, mientras que un valor del vector indica la mínima concentración correspondiente al tipo I comentada en la tabla 2.2.

Para encontrar la longitud del vector se puede definir a como su valor normalizado.

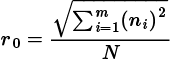.(2.3)

Por lo que se define que para encontrar el factor de concentración se puede utilizar la expresión:

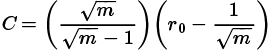.(2.4)

Reemplazando (2.3) en (2.4) se obtiene la expresión matemática para determinar el factor de concentración propuesto por Bao & Redish (2001):

.(2.5)

Vale la pena resaltar que el hecho de que el examen sea de selección múltiple restringe que el valor de m sea mínimo 2, así mismo, se puede analizar que de la ecuación anterior surge la restricción que N > m para que no se indetermine la ecuación.

Al realizar la comparación en las respuestas de los pre y post test, se puede encontrar una variación en los patrones de respuestas que sugiere hacer un análisis del factor de concentración y el score (puntajes de cada opción de respuesta). Para hacer dicho análisis se requiere emplear un código de dos niveles para lograr una caracterización del score y la concentración, este patrón de respuesta da cuenta de la medida del desempeño académico de los estudiantes y de si ellos tienen ideas previas dominantes antes de abordar cierta temática, así mismo, la variación de dicho patrón de respuesta indica si cambian o evolucionan esas ideas previas y el estado de los estudiantes con el desarrollo de las actividades. La caracterización del score y la concentración se puede dar en distintas combinaciones, un primer ejemplo es obtener en las respuestas a una pregunta un score bajo, pero una concentración alta que se denotará por medio del tipo LH (Low, Score Bajo-High, Concentración Alta) lo cual indica una fuerte tendencia a un modelo incorrecto del fenómeno analizado, por otro lado, se puede encontrar una caracterización de tipo LL que indica que la mayoría de los estudiantes no tienen un modelo dominante sobre un fenómeno y se podría considerar que las respuestas fueron tomadas al azar, la ventaja de encontrar scores de tipo LH en un pre test es que el docente puede identificar los modelos iniciales incorrectos y prepararse para saber cómo orientar el desarrollo de su propuesta académica; al comparar los resultados de los pre y post test en este análisis de la variación en los patrones de respuesta se pueden encontrar variaciones de tipo LH en el pre prest a LH en el post test, esto implica que en el desarrollo de la actividad académica se tienen determinados problemas que llevan a los estudiantes a una dirección incorrecta; otra variación puede ser de tipo LH en el pre prest a HH en el post test que indicará que el desarrollo de la actividad académica ha sido exitosa; otra posible variación del patrón puede ser de tipo LH en el pre prest a MM en el post test (Medium, Score medio-Medium, Concentración media) que indica que la actividad académica todavía no es exitosa, pero va por buen camino, de acuerdo con los planteamientos de Bao & Redish (2001) los diferentes tipos de respuestas se pueden describir conforme a las siguientes categorías de acuerdo a los modelos.

• Un modelo si la mayoría de las respuestas están en una sola opción de respuesta.

• Dos modelos si la mayoría de las respuestas están en dos opciones, generalmente una opción correcta y otra incorrecta.

• Sin modelo si las respuestas están distribuidas en tres o más opciones de respuesta.

Para cuantificar cada uno de los modelos anteriores (Low, Medium, High) es necesario tener un esquema de tres niveles para el score y la concentración de acuerdo con los promedios de los porcentajes en las respuestas correctas para cada pregunta, lo cual mostrará la dominancia de la cantidad de modelos conceptuales de esa población.

Tabla 2.2. Combinación del score y el factor de concentración.
Estilo	Nivel	Implicaciones score-concentración
Un modelo	HH	Un modelo correcto
Un modelo	LH	Un dominante modelo incorrecto
Dos modelos	LM	Dos posibles modelos incorrectos
Dos modelos	MM	Dos modelos populares, uno correcto y otro incorrecto
Sin modelo	LL	Situación aleatoria

Del factor de concentración, por ejemplo, C = 0 corresponde a una selección al azar de respuestas, C = 1, corresponde a que todos los estudiantes seleccionan la misma respuesta. Si C = 0.5 se tiene concentración alta, ya que más de 60% de los estudiantes ha seleccionado la misma respuesta. Si C = 0.2 < 0.5 indica que la población posee dos modelos de selección y un valor de C = < 0.2 da cuenta de una distribución de por lo menos tres modelos o de tendencia al azar. Mientras que para el score S se tendrá un valor bajo si S está entre 0 y valores menores a 0,4. Medio si S está entre 0,4 y valores menores a 0,7 y Alto si S está entre 0,7 y 1. La información anterior se puede codificar mediante la siguiente tabla.

Tabla 2.3. Codificación de tres niveles para el score y el factor de concentración.
Score (S)	Factor de concentración (C)	Nivel
0 < 0.4	0 – < 0.2	Low-Bajo
0.4 < 0.7	0.2 < 0.5	Medium-Medio
0.7 – 1	0.5 – 1	High-Alto

De acuerdo con Bao & Redish (2001), el patrón de respuestas permite medir el desempeño académico de los estudiantes y determinar si ellos también han superado los errores conceptuales, de modo que la variación en estos patrones de respuesta muestra cómo evoluciona el estado de los estudiantes con el desarrollo de la actividad académica utilizando Clases Demostrativas Interactivas.

Con las respuestas de los estudiantes se obtiene información tanto del Score (S) y del factor de concentración (C) estas respuestas y su variación se pueden representar mediante un gráfico de C vs S, en estos gráficos se pueden describir varias regiones, unas permitidas y otras no, de acuerdo con cada uno de los tipos de modelos. Estas combinaciones del Score y la concentración solamente pueden coexistir en una determinada región del gráfico C vs S, según Bao & Redish (2001) esta región tiene unas condiciones de frontera mínima y máxima que se pueden calcular matemáticamente mediante funciones (C en función de S) en su publicación plantean un ejemplo de un análisis para una pregunta de selección múltiple con única respuesta de cinco opciones (m = 5), de la cual se tiene la respuesta de 100 estudiantes (N = 100), se tienen N-S respuestas libre para ser distribuidas entre las cuatro opciones de respuesta restantes, la condición de frontera mínima para C se obtiene cuando las N-S respuestas están distribuidas entre las cuatro respuestas, mientras que la condición de frontera máxima C se obtiene cuando las N-S están concentradas en una de las cuatro opciones; las expresiones matemáticas para determinar las curvas mínima y máxima para el ejemplo planteado son:

,(2.6)

.(2.7)

Las curvas de frontera se pueden observar en la figura 2.1, en la cual la línea azul representa el límite superior para las concentraciones y la línea roja el límite inferior, y ningún valor para la concentración puede estar fuera de la región permitida, así mismo, se muestran las regiones en las cuales se tienen diferentes situaciones de concentración: LL (sin modelo) MM (dos modelos) y HH un modelo asociados a tres posibles condiciones.

I. Región aleatoria: Sin modelo dominante.

II. Región de dos modelos: Con dos modelos populares (con posibilidad de uno correcto y otro incorrecto).

III. Región de un modelo: Con un modelo dominante (sin ser estrictamente el correcto).

Figura 2.1 Región permitida para el factor de concentración.

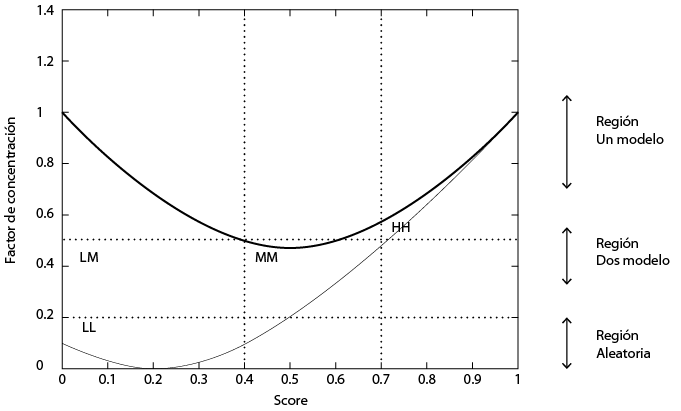
De la figura anterior se puede inferir que la región I representa los modelos con menor Score y menos Concentración LL (Región Aleatoria) la región II muestra los modelos de Score y Concentración Media LM y LM (Región dos modelos) y la región III HH es la ideal para encontrar en los post tests, ya que muestra los Score y Concentración altos, lo cual permitiría concluir que la propuesta e intervención en el aula ha sido exitosa y aplicada de manera adecuada.

2.4.5 Factor Γ: concentración de las respuestas incorrectas

Por otro lado, está el planteamiento del análisis de la concentración de los errores, que a diferencia del factor de concentración no da cuenta de la estructura general de las respuestas de los estudiantes ni depende absolutamente del score de los mismos, sino que se centra en analizar la distribución de las respuestas incorrectas del grupo, para poder determinar si en un grupo existe alguna concentración de errores que permita evidenciar un patrón que lleve a la identificación de concepciones erradas generales, dicho planteamiento se sintetiza en la definición de una variable Г que demuestra la concentración de las desviaciones en las respuestas de un test de selección múltiple con única respuesta, esta variable Г se puede calcular mediante la expresión:

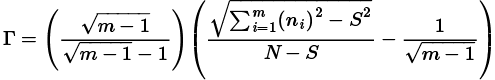.(2.8)

Donde m representa el número de opciones en las respuestas de un test, N la cantidad de estudiantes que resuelven el mismo, y S la cantidad de estudiantes que aciertan una determinada pregunta, a diferencia de la variable S utilizada para determinar límites superior e inferior en un gráfico C vs S no se obtendrá el Score S como:

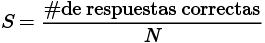.(2.9)

Sino sólo se tomará S como el número de respuestas correctas en una pregunta. De esta forma se posibilita generar un gráfico de Г vs S, dicha gráfica dará cuenta en el pre test de la incidencia en las respuestas de los estudiantes por parte de los distractores, conocimientos previos y opciones de respuesta que describen un modelo mixto. Asimismo, para el caso de las concentraciones de las respuestas erradas en el post test darán cuenta si éstas continúan, de ser así se deberá a que aun después del trabajo propuesto para cada grupo los estudiantes siguen siendo afectados por estos distractores o sus conocimientos previos continúan arraigados en sus concepciones de los fenómenos.

Es necesario tener en cuenta que para realizar el cálculo de la concentración de errores Г, sus valores deben tener un rango entre [0 y 1] y según Bao & Redish (2001) es necesario tener en cuenta que cuando un dato de la variable Г es cercano o igual a 0, la concentración de respuestas incorrectas es muy dispersa y no se podrá identificar un concepto errado general y común en el grupo de estudiantes, mientras que en los casos en la variable Г tenga un valor cercano o igual a uno 1, la concentración de respuestas incorrectas se encuentra concentrada en una respuesta errónea y se podrá identificar un concepto errado general y común en el grupo de estudiantes.

Un factor de correlación bajo es el reflejo de un cambio conceptual deficiente, un factor de correlación alto significa un cambio conceptual excelente. Existen, además, otras “variables ocultas” que modifican los valores de la ganancia de Hake tales como habilidad matemática, habilidad espacial, razonamiento científico, IQ, motivación, género, grupo cultural de referencia, dominio del lenguaje, repetición, nivel de aspiraciones académicas, participación en actividades extraescolares, horas semanales dedicadas al estudio, horas semanales dedicadas a actividades extraescolares, horas semanales dedicadas a ver la televisión, etc., entre otras que ejercen un fuerte impacto en los resultados obtenidos (Hake, 1998). Se piensa que los efectos de las variables ocultas se pueden encontrar dentro de una parte de las dos desviaciones estándar promedio de las ganancias normalizadas.

2.4.6 Análisis de Rasch

El análisis de Rasch es una poderosa herramienta para obtener información de cada reactivo por cada estudiante, y no sólo un promedio global como lo hace la ganancia de Hake. Para realizar el análisis de un test de selección múltiple existen diferentes formas que corresponden a distintos modelos, uno de ellos es el modelo de la teoría clásica de los tests, el cual puede ser utilizado en la validación local de los tests utilizados mediante el método de correlación de matrices (método de mitades partidas) y el coeficiente alfa de Cronbach que indica la confiabilidad en términos de la consistencia interna para un instrumento de medición (Becerra, 2018, pp. 158-161). Otro modelo utilizado para el análisis de las respuestas de un test es el modelo correspondiente a la teoría de respuesta al ítem, que según Muñiz (1997) fue planteado como un enfoque en la teoría de las pruebas que posibilita superar algunas de las limitaciones de la teoría clásica de los test, ya que este enfoque se centra más en las propiedades individuales de las preguntas de un test que en las propiedades generales del mismo y dos de sus objetivos generales son:

1. Proporcionar mediciones de las variables psicológicas y educativas que no estén en función del instrumento utilizado.

2. Disponer de instrumentos de medida cuyas propiedades no dependan de los objetos medidos, que sean invariantes respecto de las personas evaluadas.

Dentro de estos modelos de la teoría de respuesta al ítem se encuentra el modelo estadístico de Rasch, en el cual se obtienen estimaciones de los parámetros de cada respuesta que no son tan dependientes de la muestra de los grupos, para este caso experimental y de control, el modelo de Rasch, según Tristán (1998) es un modelo que establece la probabilidad de acertar una respuesta de un test por una persona ante un estímulo dado, en términos de la diferencia entre la medida del rasgo de una persona y la medida del estímulo utilizado; se resalta que este modelo es un modelo estocástico (no determinista) en el que la medida del rasgo de la persona y la medida del estímulo aplicado quedan ubicadas en una misma escala lineal con un origen común, sin embargo, Wu et al. (2016) comentan que existe un caso dicotómico para el modelo de Rasch, el cual se refiere al caso en el que el estudiante acierta o no una respuesta en un test de selección múltiple con única respuesta, para ello se debe codificar el acierto con un valor de 1 y el desacierto con un valor de 0, en este modelo dicotómico se determina la probabilidad de que un estudiante acierte una respuesta a una pregunta, pero esta probabilidad no está dada al azar, sino que está encadenada a la habilidad o nivel del estudiante en el manejo de dicha pregunta, que puede ser conceptual o procedimental, esta habilidad se representa mediante el símbolo θ y se puede obtener mediante la siguiente expresión matemática:

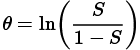.(2.10)

Donde S representa el Score o puntaje general del grupo, el cual ya se determina previamente para los análisis del factor de concentración como el cociente de la cantidad de respuestas acertadas sobre el número total de la población que presentó el test.

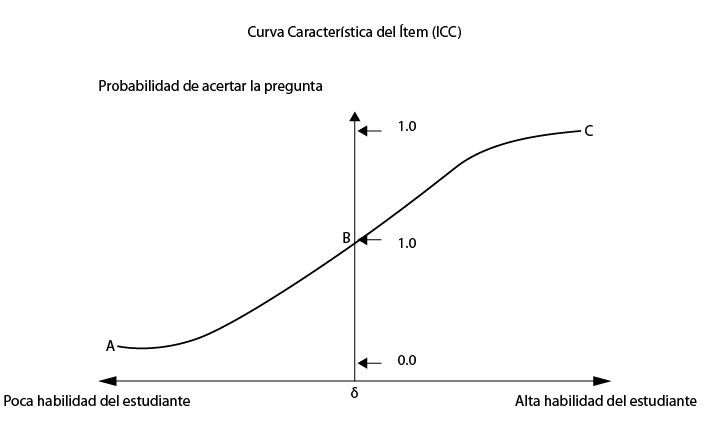
La relación mencionada previamente entre la probabilidad y la habilidad se puede caracterizar mediante una curva característica del ítem (ICC); la relación nombrada anteriormente se puede plasmar mediante una función de probabilidad, particularmente para el caso del modelo de Rasch (1980) dicha función para obtener la curva característica de un ítem para el modelo dicotómico es

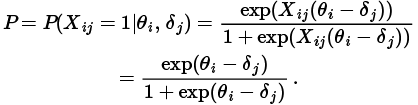(2.11)

Donde X es la variable aleatoria que indica los resultados de la pregunta, con X = 1 se tiene una respuesta correcta y con X = 0 se tiene una respuesta incorrecta, θ representa el parámetro de la habilidad del estudiante y δ en el parámetro de cada pregunta, generalmente se asocia este parámetro a la dificultad de la pregunta, al realizar la gráfica de P vs. θ de acuerdo a la ecuación (2.11) se obtiene una gráfica de la siguiente forma:

Figura 2.2 Gráfica de P vs. θ para el modelo de Rasch (caso dicotómico).