1. Introducción a los sistemas inteligentes

A través de los años, diversos autores han propuesto diferentes definiciones para el concepto de “inteligencia artificial” (ia). Boden (1977) manifiesta que Minski la definió como “la ciencia de hacer que las máquinas realicen cosas que requerirían inteligencia si fueran hechas por humanos” (p. 394). Más recientemente, Copeland (2022) define el concepto en la Enciclopedia británica como “la habilidad de una computadora digital o de un robot controlado por computadora para realizar tareas comúnmente asociadas a seres inteligentes”. Con tal diversidad de definiciones, se puede concluir que la inteligencia artificial es el conjunto de métodos y herramientas computacionales que se utilizan para resolver problemas que requieren inteligencia humana.

Los sistemas inteligentes son sistemas de software que manifiestan un comportamiento inteligente con un enfoque metodológico para resolver problemas complejos de ia en donde se obtienen buenos resultados. Un sistema inteligente emula aspectos exhibidos por el ser humano ante la naturaleza, como son, entre otros, aprendizaje, razonamiento, capacidad de comunicación, tolerancia y adaptabilidad a la imprecisión e incertidumbre.

Un sistema inteligente puede ser implementado con un enfoque o método de computación dura (menos común) o de computación suave (soft computing). En el enfoque “duro”, para resolver problemas predomina el uso de lógica binaria (crisp), análisis numérico, modelos probabilísticos, programación matemática y funcional, etc. El enfoque “suave” se enfoca más en el análisis y diseño de sistemas inteligentes usando principalmente técnicas de redes neuronales, lógica difusa, algoritmos genéticos y razonamiento probabilístico.

1.1 Computación suave

Algunos problemas representan tal grado de complejidad que requieren el uso de diferentes técnicas inteligentes como lógica difusa, redes neuronales y algoritmos genéticos. Según Negnevitsky (2005), cuando se combinan varias de estas tecnologías para implementar sistemas inteligentes híbridos que sean capaces de razonar y aprender en ambientes inciertos e imprecisos, se hace referencia al concepto de “computación suave”.

A diferencia de la inteligencia artificial convencional, que trabaja y manipula números (datos duros) y símbolos principalmente, la computación suave opera con palabras (datos suaves) que permiten trabajar de una manera más natural con información incierta, imprecisa e incompleta, lo cual es muy común en problemas de la vida real. En otras palabras, la computación suave intenta modelar nuestra forma de razonar, aprender, comunicarnos y tomar decisiones por medio de un grupo de tecnologías inteligentes. A continuación, se presentan tres de las más populares: sistemas difusos, redes neuronales y algoritmos genéticos.

1.2 Sistemas difusos

Historia

Los sistemas difusos se basan en la lógica difusa (Fuzzy Logic), también conocida como “lógica borrosa”, la cual fue inicialmente propuesta en los años 30 por Jan Lukasiewickz (1930), con el nombre de “lógica de posibilidades”. En su trabajo, Lukasiewickz introdujo una lógica que extendía los valores de la verdad a un rango similar al de los números reales entre cero y uno. Para esto, un valor en este rango representaba la posibilidad de que un evento fuera verdadero o falso. Por ejemplo, una temperatura de 40 grados Celsius podía ser considerada “caliente” con 0.92 de valor de posibilidad.

Poco después, en 1937 Max Black publicó el artículo titulado “Vaguedad: Un ejercicio de análisis lógico”. En este trabajo, Black argumentaba que un valor continuo (continuum) implicaba un grado. Él con su trabajo expresaba que la vaguedad es un concepto también sobre probabilidades, lo cual explicaba con el ejemplo de que si tenemos un tronco de madera el cual poco a poco se va convirtiendo hasta llegar a ser un sillón de lujo, podríamos referirnos a cada transformación del tronco como un grado que va incrementándose hasta convertirse en el sillón. En el apéndice, Black proponía una lógica de conjuntos difusos, tal vez su mayor contribución.

Finalmente, en 1965 estos trabajos fueron extendidos por Lofti Zadeh para crear así un sistema formal de lógica matemática, el cual fue publicado en su famoso artículo “Conjuntos difusos (Fuzzy Sets)”.

Fundamentos

La lógica difusa (Fuzzy Logic) viene a ser un conjunto de principios matemáticos para representar el conocimiento basado en grados de membrecía. A diferencia de una lógica tradicional —como la lógica booleana, que solo admite dos únicos valores (cero y uno)—, la lógica difusa opera con un rango entre 2 valores, que normalmente son el cero y el uno. En la figura 1 se puede ver de forma gráfica esta diferencia.

Un conjunto difuso es un conjunto con límites vagos, donde los conjuntos pueden tener nombres, por ejemplo, para referirse a la temperatura de una temporada es posible representar conjuntos llamados Baja, Normal o Alta, como se muestra en la figura 2. Un conjunto difuso en una computadora se representa como una función que transforma los elementos de un conjunto (por ejemplo, temperatura Baja), en un valor respectivo en grados de membrecía (eje vertical). Típicamente las funciones de membrecía usadas en los sistemas expertos difusos son representadas por triángulos y trapecios (véase figura 2).

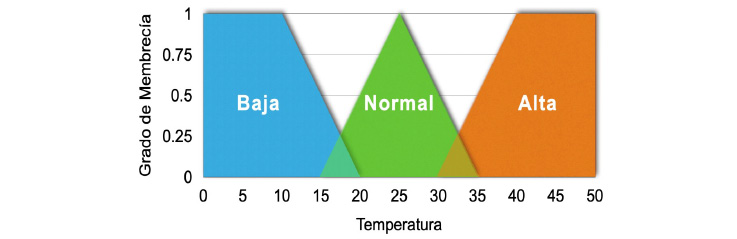
La lógica difusa se compone también de variables lingüísticas como Temperatura y valores lingüísticos como Baja, los cuales se usan para describir términos o conceptos con valores vagos o difusos. Esos valores se representan después en los conjuntos difusos.

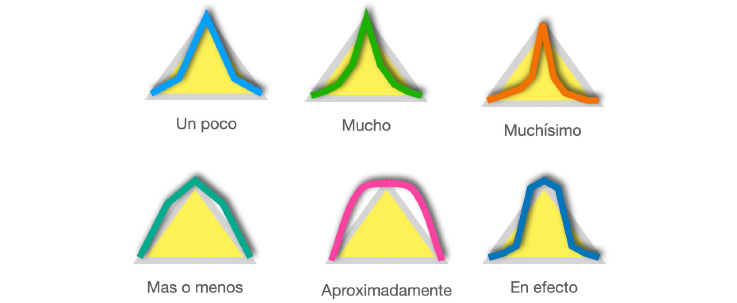
Los cercos (hedges) son calificadores de conjuntos difusos usados para modificar la forma del conjunto difuso, esto con el fin de dar una mayor flexibilidad y/o amplitud de expresión del lenguaje humano. Los cercos incluyen adverbios tales como: muy, más o menos, algo, más, menos, etc. Con estos cercos se llevan a cabo operaciones matemáticas de concentración por medio de la reducción del grado de membrecía de elementos difusos. Por ejemplo, el cerco de la figura 3 ubicado arriba a la izquierda se puede referir a una temperatura “un poco normal” o a una presión “un poco alta”, mientras que el cerco ubicado abajo a la izquierda corresponde a una estatura “más o menos alta”, etc.

Las reglas difusas son usadas para capturar el conocimiento humano y para hacer inferencias o razonamientos. Una regla difusa es un estatuto condicional de la forma:

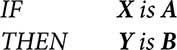
donde X y Y son variables lingüísticas y A y B son valores lingüísticos determinados por los conjuntos difusos.

Por ejemplo:

Ejemplo

Un problema usado comúnmente como ejemplo de un sistema difuso es conocido como “The Tipping Problem” y consiste en determinar el monto apropiado de propina en un restaurante. A continuación, se describe un pequeño sistema inteligente difuso que apoya a un cliente en tomar la decisión del monto de propina que deberá pagar en un restaurante considerando dos aspectos: la calidad de la comida y la calidad del servicio recibido. El sistema fue implementado usando la herramienta Matlab 7. En la figura 4 se muestran las interfaces en Matlab para el sistema difuso completo.

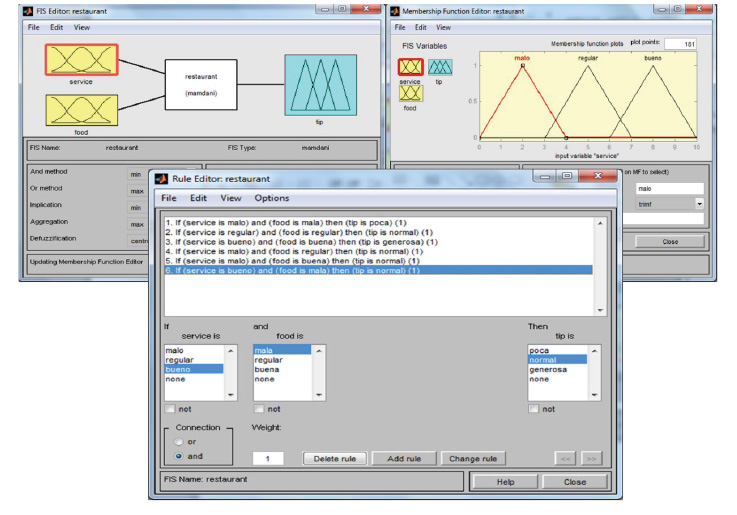
En la parte de arriba a la izquierda, aparecen las dos variables difusas o lingüísticas de entrada service (servicio) y food (comida), y la variable difusa de salida tip (propina). Por otro lado, en la sección superior derecha se observa que se definieron 3 valores difusos: malo, regular y bueno para la variable service, y en la ventana del medio aparecen las reglas difusas que evalúan el servicio y la comida para obtener la propina (poca, normal o generosa). Como se puede apreciar en la figura, la primera regla define que, si el servicio y la comida son malos, la propina es poca, y por el contrario, la regla 3 establece que, si el servicio y la comida son buenos, la propina es generosa.

1.3 Redes neuronales

Historia

Las redes neuronales forman parte de un campo más amplio llamado “aprendizaje máquina”. El aprendizaje máquina se enfoca en el diseño y desarrollo de algoritmos que permiten que las computadoras aprendan, usando para ello información proveniente de sensores o bases de datos.

Las primeras investigaciones generadas alrededor de las redes neuronales datan de 1943 (Haykin, 1999) con el neuropsicólogo Warren McCulloch y el matemático Walter Pitts con la teoría McCulloch-Pitts de redes neuronales formales. En ese tiempo se crearon grandes expectativas alrededor de esta nueva tecnología de aprendizaje máquina. Sin embargo, en el período 1969-1981 hubo una decepción general respecto a los reducidos éxitos de la inteligencia artificial, y en específico con las redes neuronales (Haykin, 1999). Fue hasta mediados de los años 80 cuando el interés en las redes neuronales volvió debido en gran medida al trabajo reportado por los investigadores Rumelhart, Hinton y Williams con el desarrollo de un algoritmo de propagación hacia atrás (back-propagation).

Fundamentos

El cerebro humano posee un aproximado de 10¹¹ pequeñas unidades conocidas como neuronas. A su vez, las neuronas se encuentran conectadas densamente entre sí, formando un estimado de 10¹⁵ enlaces, llamados sinapsis (Munakata, 2008). Una red neuronal artificial es un modelo computacional que intenta replicar parcialmente la funcionalidad del cerebro humano. Las redes neuronales artificiales, de forma muy similar al cerebro, están compuestas de neuronas artificiales y de conexiones entre ellas. La idea principal es la de imitar los procesos de comunicación entre las neuronas y su propiedad de elasticidad, fortaleciendo y debilitando las conexiones entre las mismas.

Las neuronas en este tipo de redes suelen encontrarse altamente conectadas entre sí. Cada neurona tiene un conjunto de entradas y un conjunto de salidas, que a su vez se conectan, en forma de entradas, a otras neuronas, y en conjunto se pasan información a través de las conexiones existentes entre ellas. Cada neurona emite solo una información distinta a todas las neuronas que están conectadas a ella. Sin embargo, las conexiones entre las neuronas poseen distintos pesos que determinan la intensidad con la que se recibe la información en otra neurona. De esta forma, la misma información enviada desde una neurona puede ser percibida con una fuerza distinta por diferentes neuronas, dependiendo del peso que media entre las conexiones de la emisora y las receptoras. En la figura 5 se muestra el diagrama de una neurona artificial con un conjunto de entradas, pesos y salidas.

Las redes neuronales suelen organizarse en capas, las cuales se comunican únicamente con las capas adyacentes. De esta forma, las neuronas que se encuentran en la capa de entrada solo pueden comunicarse con las que están en la capa oculta. Por otra parte, las que se encuentran en la capa oculta pueden comunicarse con la capa de entrada y la capa de salida.

El modelo computacional que define a las redes neuronales está compuesto por los parámetros siguientes: el tipo de neuronas, la arquitectura de la red y el algoritmo de aprendizaje (Kasabov, 1998).

Los tipos de conexiones que presentan las neuronas entre sí se definen como la topología de la red. Una red neuronal puede estar totalmente conectada —es decir, cada neurona está conectada con el resto— o parcialmente conectada, cuando las neuronas están conectadas solo con otras neuronas en diferentes capas. El patrón de conexiones entre las neuronas se conoce generalmente como la arquitectura de la red neuronal. De acuerdo con el número de neuronas de entrada y salida y con el número de capas de la red, es posible reconocer dos arquitecturas de conexión distintas: la autoasociativa, en la que las neuronas de entrada también son neuronas de salida, y la heteroasociativa, en la que existen dos conjuntos de neuronas: uno de entrada y otro de salida.

Otra clasificación de las redes neuronales de acuerdo con su arquitectura se obtiene considerando las conexiones de retroalimentación de la red. Si la red neuronal presenta conexiones de retroalimentación, tiene una arquitectura feedback. Las conexiones van de las neuronas de salida a las de entrada, permitiendo que la red tenga un registro de sus estados previos. Por lo tanto, el siguiente estado de la red no depende únicamente de la señal de entrada, sino también de los estados previos de la red. Cuando la red neuronal no posee conexiones de retroalimentación, entonces tiene una arquitectura feedforward o hacia adelante y propagación de errores hacia atrás (figura 6). Las redes neuronales con esta arquitectura no son capaces de recordar sus estados previos y sus salidas dependen solamente de sus entradas.

La habilidad de las redes neuronales para aprender se logra gracias a que utilizan algoritmos de entrenamiento, los cuales son llamados también “algoritmos de aprendizaje”. Los algoritmos de entrenamiento de las redes neuronales se pueden clasificar en tres categorías: aprendizaje supervisado, aprendizaje no-supervisado y aprendizaje por reforzamiento. El uso de cada uno de estos algoritmos suele ser independiente de la arquitectura de la red neuronal.

Aprendizaje supervisado. Cuando se utilizan algoritmos de aprendizaje supervisado, la red neuronal artificial recibe un conjunto de datos de entrenamiento conocido como corpus o dataset, en donde los ejemplos de entrenamiento están compuestos por un conjunto de vectores de entrada x y un conjunto de vectores de salida y (ver ejemplo en Figura 7). El proceso de entrenamiento se realiza hasta que la red neuronal aprenda a asociar el vector x con la salida correspondiente y.

Tareas como el reconocimiento de patrones y regresiones se realizan utilizando aprendizaje supervisado. También, aquellas tareas que tienen relación con información secuencial, como el reconocimiento del habla y de gestos. Se suele hacer la analogía de estar aprendiendo con un profesor, ya que se provee retroalimentación continua a las soluciones que se van obteniendo.

Aprendizaje no-supervisado. Cuando se usan algoritmos de aprendizaje no-supervisado solo se requiere el vector de entrada x, porque la red neuronal aprende las características de los vectores que se le presentan. A la red neuronal se le proporciona una función de costo con el objetivo de minimizarla. Esta función de costo es dependiente de la tarea que se está resolviendo. Con este tipo de algoritmos de aprendizaje generalmente se abordan problemas de estimación: agrupamiento, distribuciones estadísticas, compresión y filtrado.

Un tipo popular de aprendizaje sin supervisión es el aprendizaje competitivo. En el aprendizaje competitivo, las neuronas compiten entre ellas para ser activadas. La neurona de salida que gana la competencia es conocida como la neurona ganadora-toma-todo.

A pesar de que el aprendizaje competitivo fue propuesto a principios de los años 70, fue prácticamente ignorado hasta los 80, cuando Teuvo Kohonen presentó una clase especial de redes neuronales artificiales llamadas “mapas de características auto-organizadas” (Self-Organizing Feature Maps) (Kohonen, 1990). Los mapas autoorganizados (som por sus siglas en inglés) presentan un excelente rendimiento una vez que han sido entrenados. Además, los som, también conocidos como “mapas de Kohonen”, convergen rápidamente en su etapa entrenamiento y requieren de un conjunto de datos relativamente pequeño. Es importante mencionar que requieren poca cantidad de memoria y tienen buena velocidad en tiempo de ejecución. Las redes som se utilizan para diversas aplicaciones, entre ellas el agrupamiento de datos de acuerdo con ciertas características.

Aprendizaje por reforzamiento. El aprendizaje por reforzamiento es una combinación de los otros dos enfoques. A este tipo de algoritmos de aprendizaje también se le conoce como “aprendizaje de recompensa-penalización”. Algunas tareas relacionadas con este tipo de algoritmos son los problemas de control, juegos y tareas de toma de decisiones secuenciales.

Ejemplo

A continuación se presenta una red neuronal artificial del tipo perceptrón para la operación lógica OR, implementada usando la herramienta Matlab.

La figura 7 muestra los datos de entrada para que la red sea entrenada (parte izquierda ) y los datos de la salida deseada (parte derecha). Los datos de entrada son dos vectores que contienen las combinaciones posibles de los dos valores de entrada para la compuerta OR, mientras que para la salida se proporciona el vector que contiene el resultado de la compuerta OR para cada pareja de datos de entrada.

En la figura 8, por su parte, se presenta la red neuronal feedforward con tres capas; donde la capa de entrada tiene dos neuronas de alimentación, y tanto la capa del medio (llamada también “capa escondida”) como la capa de salida tienen solo una neurona cada una. La neurona va a realizar un cálculo usando dos valores de entrada (cualquier combinación de los valores cero y uno) y generará una salida de un solo valor (resultado de la operación OR) que será un uno o cero.

La red neuronal inicia un proceso iterativo de entrenamiento (operación realizada en la pestaña “Train”) donde mediante ajuste a los valores de los pesos (weights) iniciales y cálculo de la salida actual en la neurona artificial, el algoritmo de entrenamiento busca que la salida actual de la red neuronal sea igual o tenga un valor muy cercano al de la salida deseada. Cuando esto sucede, el entrenamiento finaliza y se dice que la red “ya terminó de aprender”. Después de esto la red neuronal ya está preparada para realizar operaciones lógicas OR (se usa la pestaña “Simulate”).

1.4 Algoritmos genéticos

Historia

El origen de los algoritmos genéticos se remonta a principios de la década de 1950. En esta época, un grupo de científicos de las áreas de computación y biología colaboraron para desarrollar una simulación del comportamiento de una clase de procesos biológicos. Sin embargo, fue hasta los inicios de los años 70 que John Holland y sus colegas introdujeron el concepto de “algoritmos genéticos” (Holland, 1975). Su objetivo era hacer que las computadoras hicieran lo que hace la genética. Un algoritmo genético, según la concepción de Holland, va comportándose en una forma progresiva tomando como base una población que va evolucionando por medio de “selección natural” y técnicas conocidas en la genética con el nombre de cruzamiento (crossover) y mutación.

Fundamentos

Los algoritmos genéticos (ag) son una clase de algoritmos de búsqueda no-determinística basada en evolución biológica (Negnevitsky, 2005). Dicho de manera más formal, un algoritmo genético es un proceso iterativo, el cual inicia con una población N y va generando continuamente nuevas y mejores poblaciones, usando para ello una función de evaluación de los cromosomas. Los miembros de la población son cromosomas individuales de acuerdo con el problema establecido. La función determina cuáles cromosomas son buenos y cuáles no. El área principal de aplicaciones de los ag es la búsqueda de soluciones óptimas en grandes espacios de búsqueda.

Un ag básico aplica los siguientes pasos:

1. Representar el dominio de la variable del problema como un cromosoma de longitud fija, escoger el tamaño de una población de cromosomas N, la probabilidad de cruzamiento Pc y la probabilidad de mutación Pm. Un cromosoma artificial se define como una cadena binaria que representa los “genes”.
2. Definir una función de aptitud (fitness) para medir el desempeño, adaptación o adecuación, de un cromosoma individual en el dominio del problema. La función de aptitud establece la base para seleccionar cromosomas que serán emparejados durante la reproducción.
3. Generar aleatoriamente una población inicial de cromosomas de tamaño N: x₁, x₂ , …, x_n.
4. Calcular la aptitud de cada cromosoma: F(x₁), F(x₂), …, F (x_n).
5. Seleccionar un par de cromosomas de la población actual para aparearse; los cromosomas padres son seleccionados con una probabilidad relacionada con su adaptación. Los cromosomas con gran adaptabilidad tienen una mayor probabilidad de ser seleccionados para aparearse que los de baja probabilidad.
6. Crear un par de cromosomas descendientes (offspring) para aplicar los operadores genéticos (cruzamiento y mutación).
7. Colocar los cromosomas descendientes creados como la población nueva.
8. Repetir el paso V hasta que el tamaño de la nueva población de cromosomas sea igual al tamaño de la población inicial N.
9. Reemplazar la población de cromosomas inicial (padres) con la nueva población (descendientes).
10. Ir al paso IV y repetir el proceso hasta que el criterio de terminación sea satisfecho.

Un ag representa un proceso iterativo y cada iteración se conoce como generación. Un número típico de generaciones para un ag simple va de 50 a 500. El conjunto completo de generaciones es llamado corrida (run). Al final de la corrida se espera encontrar uno o más cromosomas altamente adaptables.

Ejemplos

Un ejemplo sencillo de aplicación de algoritmos genéticos, presentado por Negnevitsky (2005), es buscar o encontrar el valor máximo de la función 15x - x², donde x toma valores enteros del 0 al 15.

Para este problema se define una población inicial de 6 cromosomas de tamaño 4 (genes), los cuales son generados aleatoriamente (note que esto representa un posible valor solución). A continuación, aparecen los 6 cromosomas de la población inicial:

X1: 1100

X2: 0100

X3: 0001

X4: 1110

X5: 0111

X6: 1001

Tomando la función 15x - x² como función de aptitud y evaluando uno a uno los 6 respectivos cromosomas (Xs), se genera un porcentaje o radio para cada cromosoma (véase tabla en figura 9). Para seleccionar pares de cromosomas para cruzarse, se puede utilizar una técnica llamada de “selección por ruleta” (roulette wheel selection) que se muestra en la figura 9.

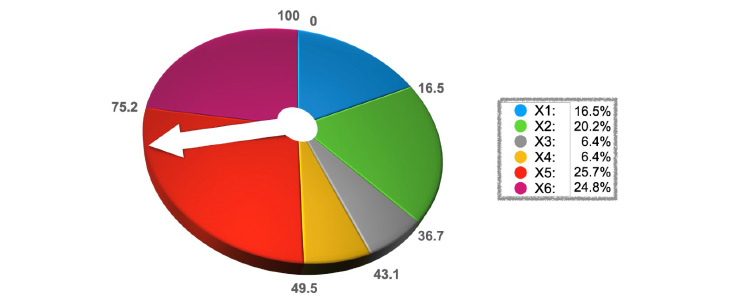
Una vez que se seleccionan tres pares de cromosomas por medio de la ruleta y que se realizan las operaciones de cruzamiento y mutación, los cromosomas que se obtienen pasan a formar la nueva población.

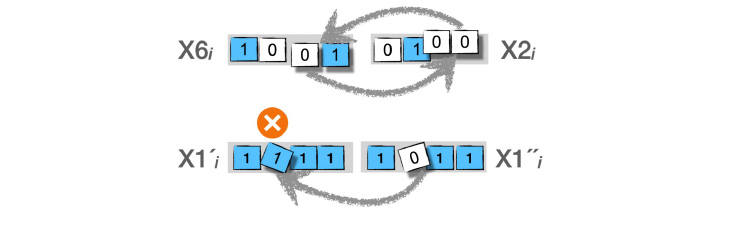
En la parte superior de la figura 10 se muestra como dos cromosomas cruzan sus respectivos genes (01 con 00), mientras que en la parte inferior se muestra una mutación de un gene (1 por 0) en un cromosoma. Estas dos operaciones, cruzamiento y mutación, generan una nueva población, la cual nuevamente es evaluada por medio de la función de aptitud para entonces seleccionar nuevamente 3 pares de cromosomas. Al final de cierto número de generaciones quedará una población con solo cromosomas 0111 y 1000, que representan los valores máximos para la función 15x - x².

1.5 Sistemas inteligentes híbridos

Los tres sistemas inteligentes estudiados (sistemas difusos, redes neuronales artificiales y algoritmos genéticos) cuentan con fortalezas, pero también con debilidades, y cada uno de ellos tiene su propia área de aplicación.

Los sistemas difusos son una excelente opción para problemas en donde se requiere representar conocimiento, manipular información imprecisa o incierta, además de comunicarse con los usuarios en forma muy expresiva y natural. Sin embargo, son ineficientes respecto a problemas donde se requiera aprender y adaptarse a procesos nuevos. Por otra parte, las redes neuronales artificiales son la mejor opción para trabajar con problemas que requieren aprendizaje y adaptabilidad, pero no son una buena opción para representar conocimiento y son una especie de caja negra, por lo que difícilmente manejan bien aspectos de explicación o comunicación con el usuario. Por último, los algoritmos genéticos son la mejor opción para problemas de optimización y representan bien el conocimiento de un experto, pero no son buenos en descubrir nuevo conocimiento.

Desafortunadamente, en el mundo real los problemas que pueden ser resueltos mediante técnicas de sistemas inteligentes son de tal complejidad que difícilmente una sola tecnología es suficiente, y por ello se requiere la combinación de las fortalezas de dos o más tecnologías inteligentes. Este tipo de sistemas se conocen como “sistemas inteligentes híbridos”.

Ejemplos

Los sistemas neuroexpertos combinan una base neuronal de conocimientos, un extractor de reglas y una máquina de inferencias, todo esto dentro de un sistema experto. Una ventaja de estos sistemas es que para hacer el trabajo que hace un experto no requieren revisar todas las reglas necesarias, que es lo que hace un sistema experto tradicional. La base neuronal de conocimientos ayuda a extraer solo las reglas necesarias para tomar decisiones.

Otro ejemplo son los sistemas neurodifusos, que mezclan un conjunto de reglas difusas junto con su manejo de inferencias dentro de una red neuronal de cinco capas. Las ventajas que contienen las redes neuronales en cuanto a aprendizaje y adaptabilidad se suman a las ventajas de representación y comunicación de conocimiento e información de un sistema difuso.

Un tercer ejemplo de sistema inteligente híbrido son las redes neuroevolutivas, las cuales aplican un algoritmo genético para mejorar iterativamente una red neuronal. Esto es muy importante debido a que el diseño de una red neuronal (topología, número de capas, pesos entre neuronas, etc.) es un trabajo más artesanal que de ingeniería. La fortaleza de un algoritmo genético para encontrar soluciones óptimas puede ayudar a encontrar la mejor red neuronal artificial para un problema dado.