10. La práctica docente de un investigador en formación en educación matemática en tiempos de pandemia

Martha Leticia García Rodríguez*
William Enrique Poveda Fernández**

DOI: https://doi.org/10.52501/cc.164.10

Resumen

El COVID-19 impactó la forma de desarrollar todas las actividades profesionales, la actividad docente no fue la excepción, los profesores vieron modificada su práctica para dar continuidad a los procesos de enseñanza y aprendizaje. El objetivo de este capítulo es analizar las dimensiones de planificación, implementación y validación de la práctica docente de un profesor en formación en educación matemática durante la pandemia. La práctica docente se asume como una actividad en continua evolución, su alcance no se limita a lo que ocurre en el salón de clases, sino que también comprende la intervención pedagógica previa y posterior a las interacciones en el aula. Se siguió el método de estudio de caso y la validez de los hallazgos se sustenta en las evidencias recabadas mediante videograbaciones, entrevista al profesor y planeaciones didácticas realizadas por él mismo. Los resultados muestran que el profesor se adaptó a las recomendaciones actuales de enseñanza acerca de las teorías asumidas para la toma de decisiones para abordar su práctica docente; tomó consciencia de la importancia del razonamiento geométrico, en la formación de los estudiantes, y su proceso formativo coadyuvó para que identificara el modelo de van Hiele para caracterizarlo. También reconoció en el ambiente de geometría dinámica un potencial para el desarrollo del razonamiento mediante el establecimiento de conexiones entre los procesos de visualización y justificación.

Palabras clave: práctica docente, modelo van Hiele, ambiente de geometría dinámica.

Introducción

Hoy en día se encuentra una vasta literatura en la que se documenta el impacto del COVID-19 en diferentes ámbitos del sector educativo, el incremento en el uso de tecnologías digitales en educación (Alabdulaziz, 2021; Pozo et al., 2021), las actitudes de los docentes hacia las tecnologías de la información y la comunicación (tic) (Chiecher, 2022), la práctica docente (Márquez de León, 2022) y estudios en los que se analiza la respuesta subjetiva de diversos actores ante la ruptura de la normalidad en el ejercicio de las actividades educativas (Cervantes et al., 2022).

La llegada de la pandemia provocó que la mayoría de los profesores de diferentes países adoptaran una enseñanza virtual para dar continuidad al proceso de formación de sus estudiantes. Para esto, hicieron uso, algunos por primera vez, de diversas tecnologías digitales, sin embargo, esto no ocurrió de la misma forma en todos los países; hoy se reconoce que existen enormes desigualdades de acceso y conectividad (Pozo et al., 2021). En lugares con suficiente conectividad, infraestructura y recursos las instituciones educativas dieron un giro hacia el aprendizaje en línea (Alabdulaziz, 2021). Un ejemplo es el caso de Arabia Saudita, donde la educación en línea se ha expandido considerablemente por efecto de la pandemia.

Ya antes de la pandemia se habían identificado en los profesores diferentes actitudes hacia las tic. Chiecher (2022) realizó una investigación para conocer mediante un cuestionario las actitudes y percepciones de un grupo de profesores universitarios de distintas áreas disciplinares y universidades, acerca de las tic y la enseñanza virtual antes y durante la pandemia. La autora identifica durante la pandemia un cambio favorable en las actitudes de los docentes ante las tic; los participantes en su investigación manifestaron que aquellos que rechazaban o eran indiferentes al uso de las tic antes de la emergencia sanitaria, durante ella se vieron obligados a acercarse a las tecnologías, conocerlas y usarlas, e identificaron en ellas utilidad para continuar con la enseñanza. De esta forma, los profesores se abocaron a aprender a usar numerosas herramientas digitales, aun aquellos que contaban con poca o nula experiencia, esto les permitió diseñar y concretar su práctica docente con el uso de las tecnologías digitales.

Márquez de León (2022) presenta un panorama de los ajustes que tuvo la práctica docente en sus dimensiones: procesos y estrategias de comunicación, planeación y estrategias didácticas, recursos o materiales didácticos, evaluación de los aprendizajes y estrategias de retroalimentación y participación de los padres de familia o tutores ante la llegada del COVID-19. Para esto realizó 15 entrevistas a maestros de educación básica de zonas urbanas y rurales de Durango, Jalisco, Querétaro, San Luis Potosí, Tamaulipas y Zacatecas. A partir de las narrativas de los profesores los autores identificaron tres tipos de práctica docente: práctica docente a distancia plena, práctica docente limitada y práctica docente híbrida o mixta. En la práctica docente a distancia las clases se realizaron en forma virtual, utilizando principalmente Google Suite, Meet, Zoom, Facebook y WhatsApp, tanto maestros como estudiantes tenían acceso a internet, lo que se tradujo en una comunicación fluida. Los docentes realizaron una planeación didáctica acorde con la modalidad virtual; se utilizaron recursos de audio y video, la evaluación se llevó a cabo mediante técnicas e instrumentos adaptados a la modalidad. En este grupo se contó con la participación de los padres de familia o tutores.

Para recuperar los significados de un grupo de estudiantes de un posgrado en investigación educativa en torno a la emergencia sanitaria ocasionada por el COVID-19, Cervantes et al. (2022) llevaron a cabo una investigación con 15 estudiantes. Mediante observación participante, un diario de notas y el análisis de documentos, los investigadores recuperaron los significados de los participantes desde una mirada endógena, situada y plural. Los participantes manifestaron concebir su proceso formativo en un clima de dificultad y satisfacción, un reencuentro con su espacio íntimo, la posibilidad de pasar tiempo en casa y convivir con su familia. En contraste, en el ámbito profesional el aislamiento caracterizó el desarrollo de las actividades, lo que dificultó el logro de los objetivos planteados en las investigaciones a realizar y provocó la necesidad de llevar a cabo ajustes al plan de actividades a realizar, el trabajo de campo, entrevistas a los participantes, entre otras.

El papel de las TIC durante la emergencia por COVID-19

En el caso particular de la educación matemática, Engelbrecht et al. (2023) se cuestionan acerca de la enseñanza de las matemáticas al terminar la pandemia, parten del hecho de que la emergencia sanitaria hizo que los docentes y los estudiantes tomaran conciencia del papel que juegan las matemáticas en nuestra sociedad; en los medios de comunicación los modelos para entender el comportamiento del virus incluían crecimiento exponencial, interpretación de gráficas y otros contenidos matemáticos que fueron utilizados para interpretar y dar seguimiento al comportamiento de la pandemia en el ámbito local e internacional. Ante esto, se reconoce la necesidad de mejorar las prácticas docentes y como parte de ellas, el proceso de diseñar el plan de clase o la instrucción resultan esenciales.

El diseño de actividades de aprendizaje es lo que permite a un profesor alcanzar los objetivos de aprendizaje en los estudiantes. Para lograrlo puede utilizar una modalidad presencial, virtual o híbrida de manera sincrónica o asincrónica, dependiendo del contexto, de los temas y de la dificultad de estos para los estudiantes. La llegada de la pandemia puso en el centro de la reflexión el papel de los estudiantes como los responsables de su propio aprendizaje (Engelbrecht et al., 2023) y a las tecnologías como aliadas indiscutibles y necesarias para llevar a cabo este proceso. Al respecto, en la literatura destaca el trabajo de Domingues y Borba (2021), quienes discuten la forma en que el estudiante aprende matemáticas con el apoyo de videos, estos últimos considerados como tecnologías digitales que han transformado el aula tradicional. Los investigadores llegaron a la conclusión de que la expresión del conocimiento matemático a través de un video posibilita que surja en los estudiantes el manejo de un nuevo lenguaje con menos rigor, pero con un objetivo más claro, lo que capta la atención de otros alumnos.

Otras reflexiones que surgieron durante la crisis sanitaria fueron abordadas por Cevikbas y Kaiser (2023), quienes se cuestionan si todo “volverá a la normalidad” o en cambio presenciaremos un auge continuo en el aprendizaje en línea en educación matemática cuando la crisis del COVID-19 termine. Los autores argumentan que existe un enorme potencial para la tecnología digital en el campo de la educación matemática, y enfocan su trabajo para responder y discutir sobre las implicaciones de las tecnologías digitales en la práctica de la educación matemática. Ellos realizaron una revisión sistemática para discutir y analizar el potencial del aula invertida como una pedagogía innovadora que involucra a los estudiantes en la educación matemática, ya que su estructura flexible y su potencial para cambiar entre diferentes métodos de instrucción tiene beneficios para la enseñanza y el aprendizaje de las matemáticas, bien sea en una modalidad en línea o una presencial. Sin embargo, también reconocen que la influencia positiva de esta pedagogía en el desempeño académico de los estudiantes depende de su autodisciplina y responsabilidad de aprendizaje. Si los alumnos no están preparados para un aprendizaje asincrónico que incluya actividades como ver videos, usar materiales de lectura o tomar notas, pueden tener dificultades en su rendimiento en matemáticas.

En los párrafos anteriores se hizo referencia a dos efectos de la pandemia en las labores educativas, el primero tiene que ver con las prácticas de los docentes que se vieron modificadas para poder dar continuidad a los procesos de enseñanza y aprendizaje incorporando el potencial de las tic, y el segundo, con el cambio en la práctica docente que realizaron los profesores en activo y en formación para adaptarse a los nuevos escenarios provocados por la pandemia. Este trabajo se ubica en el conocimiento de la práctica docente de un profesor en formación en educación matemática durante su labor en tiempos de pandemia, como el punto de partida para identificar y reflexionar en los elementos que pueden ser replicados en época de pospandemia con resultados favorables. El objetivo fue analizar las dimensiones de planificación, implementación y validación de la práctica docente de un profesor en formación en educación matemática durante la pandemia con el propósito de dar respuesta a la pregunta: ¿cuáles son los elementos de la práctica docente de un profesor que le permiten dar continuidad a su labor en el aula ante una contingencia que modifique su práctica cotidiana?

Marco de referencia

La práctica docente, según Barrón (2015), se refiere a la labor de enseñanza que realiza una persona en el aula con el fin de lograr que sus estudiantes aprendan. Esta práctica implica el uso de diversas estrategias didácticas, técnicas y recursos pedagógicos que permitan al docente garantizar el aprendizaje de sus estudiantes, así como la evaluación constante del proceso de enseñanza aprendizaje para determinar su efectividad y realizar los ajustes necesarios en caso de que se requiera. Este concepto se relaciona con información teórica y empírica que permita entender lo que sucede en la práctica, identificar problemas y resaltar soluciones para mejorar la calidad de la educación.

La práctica docente, como objeto de estudio, se basa en teorías y en una construcción metodológica y empírica de acuerdo con las necesidades y tendencias de la investigación. Montes et al. (2017) afirman que:

Construir las prácticas docentes como un objeto de estudio implica conocer tanto los referentes conceptuales usados como las diversas formas en que se abordan: los marcos metodológicos, enfoques, métodos, diseños e instrumentos utilizados; y, sobre todo, cómo son esas prácticas (p. 199).

Las teorías asumidas por los docentes pueden ser modificadas y/o enriquecidas a lo largo de su carrera profesional y son fundamentales en su toma de decisiones y en su forma de enseñar, así, “[…] las teorías asumidas corresponden a la plataforma básica sobre la que el profesor aborda su práctica docente” (García-Cabrero et al., 2008, p. 9).

Una teoría permite establecer una base conceptual acerca de la naturaleza y función de la práctica docente, así como de los factores que influyen en su desarrollo y efectividad. De esta manera, se pueden definir categorías conceptuales, hipótesis de trabajo y modelos explicativos que orienten el trabajo en el aula. En la parte empírica se debe tener en cuenta que cada docente decodifica y codifica los saberes para ser trabajados con sus estudiantes e interactúa con ellos mientras conduce las sesiones de trabajo en el aula. De acuerdo con Schoenfeld (1998), los procesos que ocurren previos al trabajo en el aula se actualizan constantemente durante la interacción con los contenidos, con los alumnos, con la exposición de temas o con las discusiones o debates, causando cambios en el pensamiento didáctico del profesor.

La pandemia por COVID-19 profundizó que se repensara la implementación de prácticas educativas y su impacto en las clases virtuales sincrónicas, asincrónicas o la combinación de éstas (Engel y Coll, 2022). Los mismos autores resaltan aspectos positivos sobre del uso de tecnologías digitales aprendidas durante la pandemia para aprovecharlos en el diseño de situaciones didácticas y su implementación en las aulas. Otro aspecto importante de la práctica docente es el análisis o evaluación de lo sucedido y de los hechos que resultan de la interacción maestro-alumnos y alumnos-alumnos, “[…] para ello es necesario considerar a la práctica como una actividad dinámica, reflexiva, que debe incluir la intervención pedagógica ocurrida antes y después de los procesos interactivos en el aula” (García-Cabrero et al., 2008, p. 4).

De acuerdo con lo anterior, la práctica docente se asume como una actividad en continua evolución de teorías y de metodologías. Su alcance no se limita a lo que ocurre en el salón de clases, sino que también comprende la intervención pedagógica previa y posterior a las interacciones en el aula. En esta dirección García-Cabrero et al. (2008) proponen un diseño indicativo para el análisis de los aspectos que conforman la práctica docente, en donde se identifican tres dimensiones que corresponden a las actividades desarrolladas antes, durante y después de las situaciones didácticas que ocurren en el contexto del aula escolar. Estas dimensiones son:

1. Dimensión A: en esta dimensión se encuentra todo lo relacionado con la planificación y preparación de la situación didáctica, incluyendo:
   1. La selección de los contenidos a enseñar, la elección de los recursos y materiales educativos, y la organización y distribución del tiempo y del espacio en el aula.
   2. Las expectativas que posee el profesor acerca del grupo de estudiantes.
2. Dimensión B: esta dimensión se refiere a las actividades que se desarrollan durante la situación didáctica propiamente dicha, como:
   1. La exposición del contenido.
   2. La realización de actividades prácticas, la atención a las preguntas y dudas de los alumnos, y la evaluación continua del proceso de aprendizaje.
3. Dimensión C: en esta dimensión se encuentran todas las acciones que se llevan a cabo después de la situación didáctica, como:
   1. El reconocimiento de los logros de aprendizaje.
   2. Las transformaciones surgidas en los estudiantes a partir de las acciones de enseñanza por parte del profesor.
   3. Validación, por parte del profesor, de los resultados de su práctica docente.

En la dimensión A es importante que los maestros examinen y reflexionen sobre sus propias teorías y creencias para que puedan mejorar sus prácticas y adaptarse a las necesidades de sus estudiantes. Coll y Rivera-Vargas (2019) complementan el marco de García-Cabrero et al. (2008) al mencionar que se deben tener en cuenta los cambios de las últimas décadas y sobre todo los relacionados con la incorporación de las tecnologías digitales.

Durante la implementación de la situación didáctica o dimensión B se ponen en juego diferentes enfoques pedagógicos, conocimientos disciplinares, experiencias personales y profesionales, así como valores y creencias. Los marcos de referencia que utilice el docente le permiten abordar situaciones complejas en el aula, tales como la diversidad de estudiantes, las distintas formas de aprendizaje, las diferentes problemáticas que puedan presentarse, entre otras. Además, a través del marco de referencia, el docente puede diseñar estrategias metodológicas adecuadas para lograr los objetivos de aprendizaje.

En la dimensión C se consideran los logros alcanzados en el aprendizaje después de las transformaciones surgidas en los estudiantes y en el profesor. Es importante tener en cuenta que los resultados de aprendizaje se refieren no sólo a los conocimientos teóricos adquiridos por los estudiantes, sino también a las habilidades desarrolladas a lo largo del proceso de enseñanza aprendizaje en matemáticas, y propiamente en geometría. Por ejemplo, Ponte et al. (2023) resaltan la importancia de que los estudiantes representen una situación matemática, formulen una estrategia de solución en donde pongan en juego la aplicación de las ideas matemáticas conocidas y también que formulen nuevas ideas que pueden incluir representaciones, conceptos, procedimientos o propiedades matemáticas.

Villalpando et al. (2020) hacen hincapié en que en la práctica docente es importante evaluar la manera en la que el docente imparte las clases y los resultados de aprendizaje que obtienen los estudiantes. De esta manera, se puede tener una visión más completa y precisa del desempeño del docente y su impacto en el proceso educativo. El profesor puede validar los resultados de su práctica docente mediante la recolección y análisis de datos de los logros de aprendizaje de sus estudiantes, la observación y evaluación de su propia enseñanza, y las retroalimentaciones y comentarios de sus estudiantes.

Metodología

Este trabajo se ubica en una perspectiva cualitativa, que de acuerdo con Sandoval (2002) se orienta a la comprensión de lo que otro u otros sujetos pretenden comunicar a través de sus palabras y acciones, lo que posibilita la construcción de generalizaciones que ayuden a explicar el comportamiento de personas que actúan en su ambiente natural. Los autores del presente documento interactuaron con un profesor en formación en educación matemática que se encuentra laborando en una escuela secundaria de la Ciudad de México. La validez de los hallazgos sobre la práctica docente del participante se sustenta en las evidencias recabadas mediante videograbaciones, entrevistas no estructuradas realizadas al profesor durante sesiones semanales (desde septiembre de 2019 hasta mayo de 2020), que derivaron en el diseño de las actividades y planeaciones didácticas elaboradas por él mismo. Para más detalles se puede consultar Orozco-García (2021).

La investigación se llevó a cabo siguiendo el método de estudio de caso, se abordó el objeto de estudio de la práctica del profesor en el aula durante el periodo de pandemia. Mediante este método se obtiene un conocimiento profundo de lo particular y lo único en relación con la práctica del profesor. Stake (1995) señala el caso intrínseco como aquél que viene dado por el objeto de estudio, en esta investigación sobre la práctica docente de un profesor en formación, el interés se centra en aprender del análisis de su práctica, sin intentar relacionarla con otros casos o problemas generales.

La investigación se diseñó en cuatro etapas (Elliott, 1991): planificación, implementación, observación y reflexión. En la etapa de planificación se identifica lo que se desea investigar y se localiza información relacionada con el tema, lo que conduce al análisis del problema de investigación. En la siguiente etapa se implementa un plan de acción para lograr el objetivo planteado; se recopilan datos que posteriormente serán analizados a través de diversos instrumentos. En la etapa de observación se organiza y gestiona la información recogida, y se produce un seguimiento para controlar, validar y evaluar las intervenciones. En la etapa de reflexión se analizan y evalúan los datos recopilados con el fin de sacar conclusiones del proceso.

Planificación

De la revisión de la literatura se asume concebir la práctica docente como una actividad que va más allá de lo que ocurre en el salón de clases, se considera como parte de ella la intervención pedagógica previa y posterior a las interacciones en el aula. Se adoptan las tres dimensiones propuestas por García-Cabrero et al. (2008), que corresponden a las actividades desarrolladas por el docente antes, durante y después de las situaciones didácticas que ocurren en el contexto del aula: dimensión A, en ella se incluye la planificación y preparación de la situación didáctica; dimensión B, que corresponde a actividades que se desarrollan durante la situación didáctica y dimensión C, donde se ubican las acciones que se llevan a cabo después de la situación didáctica.

Plan de acción

En esta etapa se recopilaron los datos que dan información de la práctica del profesor en el aula. Para esta investigación se solicitó la autorización al profesor en formación para grabar sus sesiones de clase; tres sesiones virtuales sincrónicas durante el periodo de pandemia. Asimismo, se le solicitaron las planeaciones didácticas que llevó a cabo asociadas con las sesiones de clase grabadas y para complementar la información se le realizó una entrevista.

Observación

En esta etapa se realizó un análisis de la información obtenida por cada uno de los medios anteriores, se realizó una triangulación de fuentes de información para complementar lo obtenido por alguno de los medios, si de algún dato surgía duda, se completó con la información desde otra fuente.

Reflexión

Del proceso de observación y análisis de la información se obtuvo una caracterización de la práctica docente en las dimensiones de planificación, implementación y validación de un profesor en formación en educación matemática durante la pandemia.

Selección y definición del caso

La selección del profesor en formación se realizó considerando dos razones fundamentales para el estudio; la primera fue su experiencia como profesor, y la segunda, el tema de investigación que se encontraba desarrollando como parte de su trabajo de tesis.

El profesor contaba con 5 años de experiencia impartiendo clases de matemáticas en los tres grados de educación secundaria. El plantel donde labora el profesor se encuentra ubicado en el área urbana de la Ciudad de México. En relación con el tema de investigación, su trabajo se orientó hacia el análisis de las manifestaciones del razonamiento geométrico en un grupo de estudiantes de tercer grado de secundaria. El profesor en formación diseñó una propuesta didáctica basada en el modelo de van Hiele y en el uso de tecnologías digitales, en particular un ambiente de geometría dinámica (agd) con el que se exploraron actividades geométricas en un entorno virtual y sincrónico a través de una plataforma de videollamadas. A través del agd se realizó la construcción y la presentación de figuras geométricas y se promovió la discusión de ideas matemáticas relacionadas con los niveles y descriptores de razonamiento de van Hiele.

Análisis de datos

Durante la pandemia, en la dimensión A, que se refiere a la planificación y preparación de la situación didáctica, el docente abordó:

El contenido matemático de las actividades. El tema matemático fue el de cuadriláteros y sus propiedades, las cuales involucran la descripción y análisis de figuras a partir de comparar sus lados, ángulos, paralelismo y perpendicularidad, los cuales se incluyen en el programa de estudios de la Secretaría de Educación Pública (sep, 2017). El docente está consciente de la importancia del aprendizaje y uso de la geometría en la vida cotidiana, además de la relevancia que tiene el uso de tecnología digital en su proceso.

El objetivo de aprendizaje de las actividades fue que los estudiantes identificaran y analizan las relaciones que tienen los elementos de un cuadrilátero y las propiedades que cumplen, para que definieran cada uno y los clasificaran en familias de figuras geométricas. Para la actividad del cuadrado se presentaron las propiedades de congruencia de lados, ángulos y diagonales, la perpendicularidad entre lados opuestos y la bisección de las diagonales. Para el rectángulo y el rombo se analizaron las propiedades de sus lados, ángulos y diagonales.

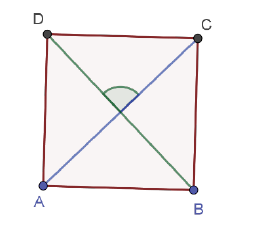
El diseño de las actividades. El profesor diseñó una actividad para el estudio de cada figura (cuadrado, rectángulo y rombo) considerando los elementos teóricos del modelo de van Hiele y el uso de tecnologías digitales. El docente creó representaciones dinámicas en GeoGebra para que los estudiantes tuvieran la oportunidad de observar los cambios de posición y medida en tiempo real cuando se arrastra alguno de los elementos de la figura geométrica. En la figura 10.1 se muestra una captura de pantalla de la representación dinámica del cuadrado incluyendo sus diagonales; el objetivo era que los estudiantes, a través de la observación y movimiento de los vértices M o N, conjeturaran que las diagonales son congruentes y perpendiculares.

Figura 10.1. Presentación dinámica del cuadrado

Para la elaboración de las actividades, el docente:

1. Utilizó las fases de diseño del modelo de van Hiele: fase 1 o presentación, se presenta a los estudiantes la figura con los elementos para analizar; fase 2 o reflexión y verbalización, se consideran las situaciones particulares producto del arrastre de los elementos de las figuras con el fin de evidenciar la propiedad; y fase 3 o formalización de vocabulario, se identifica en los estudiantes el uso correcto o no del vocabulario propio de la geometría.
2. Consideró las habilidades y conocimientos que los estudiantes deben tener al egresar de secundaria que corresponden a los tres primeros niveles del modelo de van Hiele:
   1. Nivel 1 (Reconocimiento). Los estudiantes identifican, clasifican o describen las figuras usando propiedades imprecisas; también perciben las figuras geométricas de manera global, como unidades, sin considerar sus elementos ni la existencia de clases de figuras.
   2. Nivel 2 (Análisis). En este nivel los estudiantes hacen referencia al análisis de elementos y no de figuras geométricas, describen y enuncian los elementos y propiedades de una figura geométrica de manera informal, al definir una figura enuncian propiedades necesarias, pero no suficientes, comparan figuras de manera explícita a partir de las propiedades de los elementos; reconocen relaciones matemáticas por medio de la observación de los elementos de las figuras geométricas.
   3. Nivel 3 (Clasificación). En este nivel los estudiantes identifican de manera parcial que algunas propiedades se deducen de otras, pero sin realizar demostraciones.

La elección de los recursos y materiales educativos. Todos los recursos y materiales fueron diseñados por el profesor de acuerdo al marco de referencia utilizado para el diseño de las actividades. Él creó presentaciones de la teoría para proyectarlas a los estudiantes y representaciones dinámicas haciendo hincapié en alguno o algunos de los elementos de las figuras geométricas.

En la entrevista también mencionó que incluyó representaciones dinámicas para la enseñanza y aprendizaje del tema de cuadriláteros, ya que, desde su experiencia y lo aprendido de su investigación, el uso de la función de arrastre de objetos geométricos potencia la habilidad de visualización. El arrastre de un objeto en una representación dinámica brindó a los estudiantes oportunidades para observar propiedades de las figuras.

Otra herramienta utilizada por el profesor fue la medición de los atributos de los elementos de las figuras geométricas, por ejemplo, longitud de lados, amplitud de ángulos, áreas, perímetros, entre otros; el profesor expresó que los estudiantes pueden usar esto como un recurso para verificar o refutar sus ideas matemáticas; además, indicó que cuando se utiliza la medición y el arrastre en conjunto, es posible que los estudiantes visualicen invariantes en los atributos de los objetos que conforman la representación dinámica, esto es un ingrediente fundamental para la formulación de conjeturas y, por ende, de su razonamiento matemático.

La organización y distribución del tiempo y del espacio en el aula. Estos aspectos fueron los que tuvieron las modificaciones más importantes, ya que, debido a la pandemia, las actividades se implementaron en modalidad virtual sincrónica. Al asumir que el trabajo con los estudiantes sería en una modalidad virtual, el profesor decidió diseñar previamente las representaciones dinámicas con el fin de hacer fluida y práctica la interacción con los estudiantes.

Cada actividad se diseñó para ser desarrollada en una sesión de 90 minutos utilizando la plataforma Microsoft Teams, en donde: 1. el docente mostró la representación dinámica de la figura; 2. los estudiantes exploraron la figura y el profesor orientó la discusión de las propiedades matemáticas de interés; y, 3. los estudiantes verbalizaron las propiedades utilizando el lenguaje matemático aprendido.

Según lo declarado por el docente y los datos recabados, las actividades que se desarrollaron durante la situación didáctica o dimensión B incluyeron:

La exposición del contenido y la realización de actividades prácticas. La primera actividad fue dirigida por el docente con el objetivo de que los estudiantes se familiarizaran con las representaciones dinámicas, el arrastre y la observación que conlleva a la formulación de conjeturas. En la segunda actividad, el objetivo fue que los estudiantes tomaran un papel activo en el proceso de aprendizaje al solicitar al profesor acciones concretas que permitieran conjeturar alguna propiedad o justificar ideas matemáticas basándose en el arrastre y medición que permite GeoGebra. La tercera actividad fue autodirigida, es decir, los estudiantes asumieron un rol autónomo para generar ideas matemáticas y solicitar al docente arrastrar algún elemento de la representación dinámica para refutar o validar, mediante elementos empíricos, la conjetura.

La implementación de las actividades las llevó a cabo el profesor según las fases de Corberán et al. (1994):

1. Fase 1 (Información). El docente informa a los estudiantes el tema que se va a tratar, los conceptos que serán abordados, etc., también es una etapa diagnóstica, en la que el docente identifica los conocimientos de los estudiantes sobre el tema y el nivel de razonamiento.
2. Fase 2 (Orientación dirigida). Los estudiantes conocen el campo de estudio, comienzan a entrar en contacto con elementos que representen conocimientos nuevos, que den paso a un razonamiento del siguiente nivel.
3. Fase 3 (Explicitación). Esta fase se caracteriza por la interacción que se lleva a cabo entre los estudiantes, ya que se genera un intercambio de experiencias entre ellos.
4. Fase 4 (Orientación libre). Los estudiantes aplican y combinan los conocimientos adquiridos en las fases anteriores, realizan actividades nuevas, para este momento ya cuentan con familiaridad del tema de estudio, y están en posibilidad de perfeccionar sus habilidades de razonamiento.
5. Fase 5 (Integración). En esta fase los estudiantes deben integrar los contenidos revisados de manera reciente con los que ya contaban.

La atención a las preguntas y dudas de los alumnos, y la evaluación continua del proceso de aprendizaje. El docente trabajó con los estudiantes en las actividades mediante un diálogo, los cuestionó constantemente. Para ejemplificar la forma de trabajo se presentan las siguientes actividades. En la tabla 10.1 se registra la transcripción de la conversación generada en torno a la presentación del cuadrado (actividad 1). El docente observa que en las intervenciones 1 y 2 los alumnos reconocen la figura por su nombre, esto los ubica en el nivel de razonamiento 1 de acuerdo con el modelo de van Hiele. En la intervención 3, Daniel indica el número de lados y la propiedad de igualdad entre ellos, lo que el profesor relaciona con los descriptores de un nivel 2 de razonamiento.

Tabla 10.1. Presentación de la propiedad de congruencia entre lados opuestos del cuadrado

Presentación del cuadrado
Intervención docente	Intervención	Respuesta del estudiante	Presentación de figuras
En el buzón de chat escribirán la figura que observan.	1. Adrián	Un cuadrado	Figura 2 El docente muestra una representación dinámica del cuadrado
	2. Daniel	Un cuadrado
¿Por qué dices que es un cuadrado?	3. Daniel	Porque tiene 4 lados y todos son iguales

Tabla 10.2. Presentación de la propiedad de congruencia entre lados opuestos del rectángulo

Propiedad de congruencia de lados opuestos del rectángulo
Intervención docente	Número de intervención	Respuesta del estudiante	Presentación de figuras
¿Qué figura observan?	1. Daniel	Un rectángulo	Figura 3 Presentación dinámica del rectángulo
¿Qué propiedad tienen los lados opuestos de un rectángulo?	2. Daniel	Congruentes
Si comenzamos a identificar propiedades en el mismo orden que lo hicimos con el cuadrado entonces ¿cómo son los lados opuestos de un rectángulo?	3. Adrián	Paralelos	Figura 4 Presentación dinámica del cuadrado, indicando la longitud de sus lados
Los lados opuestos son congruentes y tienen una notación gráfica, ¿recuerdan cómo se denotan?	4. Adrián y Daniel	Usando rayas, una para un par de lados congruentes y dos para los otros dos	Figura 5 Presentación del cuadrado, con simbología de congruencia entre lados opuestos.

En la segunda actividad, el docente mostró una representación dinámica del rectángulo, en la tabla 10.2 se registra un resumen de la transcripción de la conversación generada en torno a la propiedad de congruencia de los lados opuestos de un rectángulo, concluyendo con su respectiva notación matemática. El docente expresó que Daniel, en la intervención 2, y Adrián, en las intervenciones 3 y 4, identificaron las propiedades de paralelismo y congruencia entre lados opuestos del rectángulo, respectivamente. El arrastre y el movimiento ayudaron a que los estudiantes validaran sus respuestas. Las preguntas del profesor orientaron la discusión y uso de la notación matemática correcta (intervención 4).

En la tabla 10.3 se registra un resumen de la transcripción de la conversación generada en la actividad 3, en donde el profesor presenta un rombo con el fin de que los estudiantes lo reconozcan de acuerdo con sus propiedades. En la intervención 1, Adrián expresa que desconoce la definición de rombo; con ayuda del docente, Daniel comenta algunas propiedades que observa en la figura sin dar la definición. En la intervención 4, el profesor considera que Adrián aún no posee un conocimiento básico de los cuadriláteros.

Tabla 10.3. Presentación de la propiedad de congruencia entre lados opuestos del rombo

Presentación del rombo
Intervención docente	Número de intervención	Respuesta del estudiante	Presentación de figuras
¡Adrián! ¿por qué consideras que es un rombo?	1. Adrián	ah… Espéreme. No lo sé	Figura 5. Representación dinámica del rombo
¿Podrías ayudarle a Adrián a definir un rombo?	2. Daniel	Dos de sus ángulos, de cada lado son mayores que los otros dos de arriba y de abajo
¿Algo más Daniel?	3. Daniel	También podría ser que es un paralelogramo
¡Adrián! ¿Algo más?	4. Adrián	No, ya no, creo que no

Con respecto a la dimensión C en la cual el docente identifica acciones que se llevan a cabo después de la implementación de la situación didáctica, se obtuvo:

El reconocimiento de los logros de aprendizaje. Las transformaciones surgidas en los estudiantes, a partir de las acciones de enseñar por parte del profesor. De acuerdo con el modelo de van Hiele, el docente concluyó que los alumnos están en la transición entre el nivel 2 y el 3 de van Hiele, ya que tienen la mayor cantidad de descriptores del nivel 3 del modelo de van Hiele. Por ejemplo, concluyó que los estudiantes:

1. expresan en forma verbal propiedades que cumplen los componentes de las figuras geométricas a partir de la observación de éstas;
2. observan un conjunto de figuras y sacan una conclusión general;
3. expresan que las figuras tienen componentes y éstas cumplen propiedades;
4. expresan en forma verbal propiedades que cumplen las componentes de las figuras geométricas a partir de la observación de éstas, sin llegar a relacionarlas o clasificar las figuras dadas;
5. resumen, propiedades o procedimientos de lo aprendido sobre el tema y lo reflejan en sus acciones y obtienen una visión general de la nueva red de relaciones que han construido, resumen las propiedades de una figura;
6. comparan figuras mediante el uso explícito de propiedades de sus componentes, entre otras.

Validación, por parte del profesor de los resultados de su práctica docente. Como parte de las reflexiones realizadas por el profesor después de la implementación de las actividades, mencionó que, mediante la exploración de las figuras geométricas, los estudiantes dedujeron y verificaron propiedades matemáticas y participaron de manera activa, motivados al identificar relaciones entre los elementos de las figuras. Además, expresa que, dadas las respuestas de los estudiantes, asociadas con las figuras, sus elementos y sus propiedades, en un análisis más cuidadoso de éstas se observa un avance gradual en el razonamiento, según los niveles del modelo de van Hiele.

Oportunidades y desafíos

El estudio de caso que se ha presentado hizo visibles oportunidades y desafíos ante nuevas emergencias que pudieran surgir en el futuro, en esta sección se reflexiona sobre algunos de ellos.

A partir de la evidencia del trabajo del profesor en formación se pudo identificar que su aceptación a utilizar tecnologías digitales le permitió diseñar e implementar sus actividades. Combinó el uso de GeoGebra para el diseño de las mismas y con uso de Teams para la implementación y la interacción con sus estudiantes, con lo que logró una comunicación sincrónica que le permitió dar seguimiento al proceso de aprendizaje durante la pandemia, lo que coincide con lo reportado por Chiecher (2022) acerca del uso de numerosas herramientas digitales por parte de los profesores durante el confinamiento.

En relación con las dimensiones de la práctica docente propuestas por García-Cabrero et al. (2008), durante la aplicación de la situación didáctica, el docente mostró flexibilidad para realizar ajustes en su práctica docente de acuerdo con las nuevas condiciones de trabajo: 1. cambió de sesiones presenciales a virtuales sincrónicas para generar la conversación entre él y sus estudiantes; 2. consideró necesario que los estudiantes le indicaran los pasos a seguir en la exploración de las representaciones dinámicas, a partir de preguntas y cuya dificultad aumentó gradualmente, en lugar de proporcionar a cada estudiante las representaciones; y, 3. promovió las interacciones entre docente-estudiantes y estudiantes-estudiantes con el fin de crear un ambiente de confianza y debate. Los datos recabados aportan evidencia de que la planificación y el diseño de las actividades en las que se consideraron los elementos teóricos del modelo de van Hiele en una representación dinámica en un agd, permite generar objetos geométricos de tal manera que al moverlos se siguen cumpliendo sus propiedades matemáticas. Lo anterior favoreció captar la atención de los alumnos y que siguieran el desarrollo de las actividades mediante su participación. Los puntos anteriores resultaron importantes, ya que fueron el medio para que los estudiantes expresaran los rasgos de su razonamiento matemático. Las características de la práctica docente del profesor lo ubican en la categoría de práctica docente a distancia plena, de acuerdo con la clasificación de Márquez de León (2022).

Sin embargo, se identificaron desafíos que no se deben soslayar: la necesidad de contar comentarios y retroalimentación por parte de los estudiantes acerca de la práctica del profesor y que el retorno a la presencialidad evidenció la carencia en acceso y conectividad en las escuelas públicas, lo que puede derivar en un retroceso en el uso de las tic por parte de los docentes.

Conclusiones

El proceso de formación le proporcionó al docente los elementos teóricos y metodológicos que se hicieron visibles cuando se presentó la contingencia sanitaria debida al COVID-19 y que le permitieron dar continuidad a su labor cotidiana. Los elementos de su práctica docente corresponden a las dimensiones: (A) del pensamiento didáctico del profesor y a la planificación de la enseñanza; (B) la interacción educativa dentro del aula; y, (C) la reflexión sobre los resultados alcanzados, propuestas por García-Cabrero et al. (2018).

En la dimensión A se identificaron los elementos: dominio y uso de la teoría en didácticas específicas y de la parte conceptual matemática por parte del docente, los cuales resultan importantes en el proceso de identificar el avance de los estudiantes hacia el logro de los objetivos de aprendizaje. La teoría permite al docente considerar el nivel cognitivo de los alumnos durante el diseño de actividades didácticas para que estas sean adecuadas y desafiantes. El uso del modelo de van Hiele, en el caso de la didáctica de la geometría, proporciona herramientas al docente para este diseño, ya que se requiere considerar que los estudiantes necesitan transitar por diversas etapas de aprendizaje antes de alcanzar un nivel superior de la comprensión del tema.

En la dimensión B, durante la implementación de las actividades, elementos importantes fueron: la disposición e interés por parte del docente para atender las preguntas, respuestas y dudas de los estudiantes, y plantearles interrogantes para que ellos mismos llegaran al resultado correcto. Como menciona Schoenfeld (1998), la enseñanza no puede limitarse a la memorización o la repetición mecánica de procedimientos, por el contrario, el docente debe fomentar en sus estudiantes habilidades asociadas con el razonamiento y la capacidad para comunicar ideas.

Otro elemento importante fue la interacción entre el docente y los estudiantes durante el proceso de aprendizaje para crear un ambiente virtual sincrónico que favoreció el desarrollo de habilidades de razonamiento. En estas interacciones, el uso de recursos didácticos como representaciones manipulativas o dinámicas contribuyó para la comprensión en los estudiantes y para modificar la forma de enseñar la geometría por medio de la exploración y el redescubrimiento. Durante la implementación de las actividades didácticas el docente fue capaz de adaptarse a las nuevas situaciones que se presentaron en aras de continuar el proceso de enseñanza aprendizaje.

En la dimensión C, un análisis retrospectivo o evaluación de lo sucedido durante la práctica docente le permitió al maestro comprender el proceso de aprendizaje, reconocer la metodología seguida y adaptar las actividades de enseñanza para satisfacer las demandas o necesidades individuales y colectivas de su grupo. Esta evaluación contribuyó para identificar fortalezas y debilidades de las actividades, lo que se convierte en ingrediente para desarrollar nuevas estrategias y con esto mejorar la enseñanza.

A manera de reflexión final, al centrar la atención en las dimensiones de García-Cabrero et al. (2008) en las que se hace uso de teorías o marcos teóricos, en el caso de esta investigación, el modelo de van Hiele y el uso de GeoGebra, un docente de manera flexible puede adecuarse a las condiciones de trabajo, tal como sucedió en este estudio durante la pandemia y adaptar su práctica docente de acuerdo con las nuevas variables que imponga el sistema educativo o el contexto social.

Agradecimientos

Este trabajo fue posible gracias al apoyo del Centro de Investigación en Ciencia Aplicada y Tecnología Avanzada (cicata) unidad Legaria del Instituto Politécnico Nacional, a través de la Secretaría de Investigación y Posgrado en el marco de los proyectos con números 20210725 y 20220322.

Este trabajo fue posible gracias al apoyo de la Escuela de Matemática de la Universidad de Costa Rica.

Referencias

Alabdulaziz, M. (2021). COVID-19 and the use of digital technology in mathematics education. Education and Information Technologies, 26, 7609-7633. https://doi.org/10.1007/s10639-021-10602-3

Barrón, C. (2015). Concepciones epistemológicas y práctica docente. Una revisión. REDU. Revista de Docencia Universitaria, 13(1), 35-56.

Cervantes, E., Gutiérrez, P., y Ronquillo, C. (2022). Ser estudiante de posgrado en contextos de incertidumbre. La experiencia de los investigadores educativos en formación. Revista Iberoamericana para la Investigación y el Desarrollo Educativo, 13(25). https://doi.org/10.23913/ride.v13i25.1363

Cevikbas, M., y Kaiser, G. (2023). Can flipped classroom pedagogy offer promising perspectives for mathematics education on pandemic-related issues? A systematic literature reviews. ZDM Mathematics Education 55, 177-191. https://doi.org/10.1007/s11858-022-01388-w

Chiecher, A. (2022). Docentes en pandemia. Actitudes hacia las tecnologías y percepciones de la enseñanza virtual. Revista Actualidades Investigativas en Educación, 22(2), 1-30. https://doi.org/10.15517/aie.v22i2.48680

Coll, C., y Rivera-Vargas, P. (2019). Repensar la educación escolar en la sociedad digital. En Políticas públicas para la equidad social: Vol. II (pp. 13-22). Universidad de Santiago de Chile.

Corberán, R., Gutiérrez, A., Huerta, M., Jaime, A., Margarit, J., Peñas, A., y Ruiz, E. (1994). Diseño y evaluación de una propuesta curricular de aprendizaje de la geometría en enseñanza secundaria basada en el modelo de razonamiento de Van Hiele. Ministerio de Educación y Ciencia, Centro de Investigación y Documentación Educativa. https://sede.educacion.gob.es/publiventa/descarga.action?f_codigo_agc=1379_19

Domingues, N., y Borba, M. (2021). Digital video festivals and mathematics: Changes in the classroom of the 21st century. Journal of Educational Research in Mathematics, 31(3), 257-275.

Elliot, J. (1991). La Investigación-Acción en Educación. Morata.

Engelbrecht, J., Kwon, O.N., Borba, M. C., Yoon, H., Bae, Y., y Lee, K. (2023). The impact of COVID-19 on the format and nature of academic conferences in mathematics education. ZDM Mathematics Education 55, 95-108. https://doi.org/10.1007/s11858-022-01421-y

Engel, A., y Coll, C. (2022). Entornos híbridos de enseñanza y aprendizaje para promover la personalización del aprendizaje. RIED. Revista Iberoamericana de Educación a Distancia, 25(1), pp. 225-242. https://doi.org/10.5944/ried.25.1.31489

García-Cabrero, B., Loredo, J., y Carranza, G. (2008). Análisis de la práctica educativa de los docentes: pensamiento, interacción y reflexión. Revista Electrónica de Investigación Educativa, 10 (Especial). http://redie.uabc.mx/NumEsp1/contenido-garcialoredocarranza.html

Márquez de León, E. (2022). La práctica docente en tiempos de pandemia. Experiencia de los profesores de educación básica en México. En H. I. Molina, J. C. Macías y A. Cepeda (Coords.), Educación en tiempos de COVID-19: Una aproximación a la realidad en México: experiencias y aportaciones. México: Comunicación Científica. https://comunicacion-cientifica.com/wp-content/uploads/2023/02/069.-PDF2-Educacio%CC%81n-en-tiempos-de-Covid-19.pdf

Montes, L., Caballero, T., y Mirando, M. (2017). Análisis de las prácticas docentes: estado del conocimiento en DOAJ y EBSCO (2006-2016). CPU-e. Revista de Investigación Educativa, (25), 197-229.

Orozco-García, S. (2021). Caracterización del razonamiento geométrico de estudiantes de secundaria en un ambiente de geometría dinámica aplicando el modelo de van Hiele. Tesis de Maestría. Instituto Politécnico Nacional, México.

Ponte, J. P., Mata-Pereira, J., y Quaresma, M. (2023). Challenging students to develop mathematical reasoning. En J. Cai y J. Middleton (Eds.), Mathematical Challenges For All (pp. 147-167). Springer International Publishing.

Pozo, J., Pérez-Echeverría, M., Cabellos, B., y Sánchez, D. (2021). Teaching and Learning in Times of COVID-19: Uses of Digital Technologies During School Lockdowns. Frontiers in Psychology, 12, 656776. https://doi.org/10.3389/fpsyg.2021.656776

Briones, G. (2002). Fundamentos epistemológicos de la investigación cualitativa. En C. A. Sandoval (Ed.), Investigación Cualitativa (pp. 23-45). ARFO Editores e Impresores Ltda.

Schoenfeld, A. H. (1998). Toward a theory of teaching–incontext. Issues in Education, 4 (1), 1-94. https://doi.org/10.1016/S1080-9724(99)80076-7

Secretaría de Educación Pública [SEP]. (2017). Aprendizajes Clave para la Educación Integral. Matemáticas. Educación Secundaria Plan y Programas de Estudio, Orientaciones Didácticas y Sugerencias de Evaluación. https://es.scribd.com/document/650048376/APRENDIZAJES-CLAVE-Matematicas-Educacion-secundaria-Plan-y-programas-de-estudio-orientaciones-didacticas-y-sugerencias-de-evaluacion

Stake, R. E. (1995). The Art of Case Study. Sage.

Villalpando, C., Estrada-Gutiérrez, M., y Álvarez-Quiroz, G. (2020). El significado de la práctica docente, en voz de sus protagonistas. Alteridad, 15(2), 229-240. https://doi.org/10.17163/alt.v15n2.2020.07

---