10. La modelación matemática como estrategia didáctica para promover la interdisciplinariedad escolar en telesecundaria

Erika García Torres*
Felipe de Jesús Santiago Flores**

DOI: https://doi.org/10.52501/cc.132.10

Resumen

Este estudio plantea una problemática didáctica relacionada con el diseño de situaciones por parte del colectivo docente de telesecundaria en las que interactúen dos o más asignaturas, y al mismo tiempo una solución de trabajo interdisciplinar con saberes de matemáticas, biología y química. El objetivo es el diseño e implementación de una situación interdisciplinaria a través de la modelación matemática, así como la caracterización de la construcción de saberes de las y los estudiantes en dicha situación. Los resultados evidencian modelos matemáticos que tienen como característica principal los discursos matemáticos y extramatemáticos y se concluye que estas situaciones son una gran posibilidad para trabajar en las aulas de telesecundaria.

Palabras clave: modelación matemática, interdisciplinariedad escolar, situación interdisciplinaria, telesecundaria.

Introducción

Un suceso histórico por el que atravesamos desde 2020 a nivel mundial fue la pandemia ocasionada por el virus SARS-COV2 que derivó en casi dos años de no trabajar de manera presencial en las aulas con las niñas, los niños y los adolescentes, y aunque hay varias experiencias docentes que se hicieron a partir del trabajo virtual, una parte de las y los docentes no optaron por ello debido a las brechas tecnológicas que existen en la educación pública en México. Con fines de practicidad, cierta parte del colectivo docente eligió trabajar con los libros de texto gratuitos, reconociéndolos como un material fundamental para asegurarse de que todas y todos tuvieran acceso a ellos y disminuir la inequidad que tienen algunos contextos relacionados con el acceso a internet. De igual manera, la Secretaría de Educación Pública (sep) apostó por clases televisadas mediante el programa “Aprende en casa”, las cuales se basaron en los libros de texto gratuitos.

Para el cierre del ciclo escolar 2021-2022, las escuelas públicas de educación básica regresaron a la modalidad presencial enfrentándose a nuevos retos y dando respuesta a los estragos que dejó la pandemia, no únicamente relacionados con los saberes —aspectos cognitivos—, sino también con la comunicación de emociones y sentimientos por la pérdida de muchos seres humanos. A lo largo de la historia del diseño curricular, la educación en México ha apostado por abrir espacios dentro del currículo para atender este tipo de dilemas sociales, dos de los más recientes fue la creación de las asignaturas Vida Saludable y Educación socioemocional, como objetos de conocimiento. Sin embargo, tal como lo discute Coll (2006), este tipo de decisiones provoca que el currículo quede sobrecargado por la acumulación de contenidos curriculares que imposibilitan que puedan ser enseñados y aprendidos.

Aunado a lo anterior, los efectos de la pandemia coadyuvaron a que la sep planteara a principios del año 2022 una reorganización curricular en la que se aboga por las problemáticas sociales, culturales, económicas y políticas en las que están inmersas las escuelas de educación básica; es decir, que la escuela responda a las problemáticas que enfrenta cada sector social para que el aprendizaje de las niñas, los niños y los adolescentes sea situado, contextualizado, significativo e interesante. Siguiendo este discurso, el Marco Curricular y Plan de Estudios 2022 hace la crítica de que la organización curricular anterior se basa únicamente en la lógica que tienen las disciplinas escolares, sin tomar en cuenta el contexto escolar, la realidad educativa ni la diversidad de personas que interactúan en ella (sep, 2022).

Es así como se apuesta por trabajar saberes, no competencias ni aprendizajes clave, que se promovieron en los planes de estudio 2011 y 2017 (sep, 2011a; sep, 2011b; sep, 2017a); dichos saberes son entendidos como construcciones integradas con elementos provenientes de varias disciplinas, pero sistematizados y enfocados en la realidad que viven las y los estudiantes (sep, 2022), esta reestructuración de los contenidos disciplinares se basa en lo que Torres (2015) entiende por currículum integrado.

Centrándonos en el tipo de servicio de la telesecundaria en México éste ha brindado atención educativa a jóvenes entre 12 y 15 años en zonas rurales, y un docente atiende a un grado escolar, es decir, los docentes imparten todas las asignaturas del currículo del nivel secundaria. De acuerdo con los datos estadísticos de la Dirección General de Planeación, Programación y Estadística Educativa (2021), 72,157 docentes imparten clases en las telesecundarias, lo que corresponde a un 21 % a nivel nacional, quienes tienen perfiles profesionales diversos y son los encargados de llevar a la práctica las reestructuraciones curriculares.

La reestructuración curricular en saberes pudiera ser una realidad en el contexto de las telesecundarias, debido a que el docente imparte todas las asignaturas y ha desarrollado conocimientos disciplinares y sus posibles relaciones. Como reporta García (2016), los docentes de telesecundaria emplean estrategias como el uso de situaciones integradoras para vincular significados de varias asignaturas, lo que ellos denominan transversalidad. Si bien no hay una convención sobre este término, los proyectos transversales se orientan a ejes prioritarios que afectan todo el currículo (Magendzo, 1998), como medio ambiente, educación para la paz, educación moral, educación sexual, ente otros. Como señalan Otano y Sierra (en Yus, 1996), los temas transversales están dotados de elementos comunes y diferenciales que obligan a compaginar un tratamiento didáctico global con la profundización en la especificidad (de las disciplinas). Para Henríquez y Reyes (2008) es importante que los proyectos transversales tengan sentido y pertinencia, es decir, que deben ser interesantes para abordar contenidos relevantes, valiosos, necesarios para la vida, la convivencia, que den respuesta a problemas sociales para que los jóvenes le encuentran sentido a lo que están construyendo. Sin embargo, nos distanciamos del término de transversalidad pues, aunque favorece la interacción entre los aprendizajes (Palos, 1998), su tratamiento didáctico se asocia con contenidos sociales con perspectiva humanística, y en nuestra opinión queda abierta la discusión sobre las relaciones interdisciplinarias que permiten la comprensión de fenómenos.

Problemática

Reconocemos que el colectivo de docentes de telesecundaria tiene un conocimiento profesional de todas las asignaturas del currículo que imparten, y que la posibilidad de que se favorezcan los saberes entendidos como construcciones integradas con elementos provenientes de varias disciplinas (sep, 2022) es un reto para ellos. El diseño de situaciones de esta naturaleza en las que interactúen saberes escolares (de diversas asignaturas) y extraescolares recae en el colectivo docente.

Un riesgo de los proyectos transversales es que la vinculación entre las disciplinas sea el contexto de la situación problema, pero que los discursos entre asignaturas no se estén entrelazando (García, 2016). En un mundo globalizado y con problemáticas que requieren cada vez más la explicación de diversas disciplinas, es importante que los seres humanos construyan pensamientos complejos que les permitan explicar los fenómenos que los rodean. Es por ello que en este estudio problematizamos la vinculación de los contenidos que propone el currículo, lo cual es y será una práctica constante de los docentes de telesecundaria, y lo hacemos desde la llamada interdisciplinariedad escolar.

Para Roth (2014), la interdisciplinariedad denota el hecho, la calidad o la condición de dos o más campos académicos o ramas del aprendizaje. Esto quiere decir que se trata de una forma en la que dos o más campos del saber colaboran para explicar un fenómeno natural u objeto de la actividad humana, mientras que, al trasladar el término al ámbito escolar, se trata de concretar un proyecto o resolver un problema explicado desde dos o más disciplinas académicas. De acuerdo con Perera (2008), la interdisciplinariedad es una estrategia didáctica que prepara al estudiante para realizar transferencias de contenidos que le permitan solucionar holísticamente las dificultades que enfrentará, sea en su futuro desempeño profesional o en la resolución de un problema.

Para diseñar una situación en el marco de la interdisciplinariedad escolar, se requiere tener conocimientos didácticos y dominio disciplinar para asegurar que realmente se impulsen aprendizajes en las diferentes disciplinas que se relacionan; esto representa una nueva forma de tratamiento didáctico. Además, en el contexto de los saberes matemáticos se considera que un trabajo interdisciplinario debe incluir a la matemática como una forma de transformar las situaciones reales en conocimientos matemáticos y en relación con otras disciplinas. Ante ello, la modelación matemática brinda una oportunidad para hacer esta transformación debido a que se comprende como una práctica de articulación entre dos entes, uno llamado modelo, que sirve para actuar en otro, llamado lo modelado. Lesh y Caylor (2007) consideran que la modelación es una forma de actuar, diseñar, abordar y pensar en un sistema —en este caso matemático— los elementos que se hacen conscientes de otro sistema —lo modelado—.

La modelación matemática para esta investigación se postula como una estrategia de enseñanza que permite el aprendizaje de las matemáticas en relación con otras áreas de conocimiento. Para ello, el docente se convierte en un mediador y guía para la construcción del modelo matemático y el estudiante es el sujeto activo, quien autoevalúa constantemente si el modelo creado cumple con las características solicitadas.

Además, se debe partir de un problema conocido por los sujetos para que propongan modelos de solución al problema, pues son ellos quienes cuestionan, infieren y resuelven el problema (Biembengut y Hein, 2004). Por problema conocido en el contexto escolar nos referimos a uno que forme parte de la realidad de los jóvenes que participan en el estudio. Por tanto, el objetivo de esta investigación es el diseño y la implementación de una situación interdisciplinaria a través de la modelación matemática, así como caracterizar la construcción de saberes de los estudiantes que emerjan de esta situación.

Marco conceptual

En el presente apartado se discuten términos principales en esta investigación: interdisciplinariedad, situación interdisciplinaria, modelación matemática y actividad de obtención de modelos (Model-Eliciting Activity).

Williams et al. (2016) plantean que, para problematizar la interdisciplinariedad escolar, se requiere entender el significado de disciplina o disciplinariedad. Por ello, hacen una revisión histórica, en la que encuentran que la segmentación de disciplinas se hizo a partir de que los sujetos tuvieran un rol de trabajo específico, a lo largo de la historia fue necesario tener un vocabulario específico para poder entender la complejidad de los fenómenos naturales y sociales. Roth (2014) indica que la interdisciplinariedad denota el hecho, la calidad o la condición de dos o más campos académicos o ramas de aprendizaje.

Álvarez (2001) considera la interdisciplinariedad como un método ventajoso, porque permite dirigir el proceso de resolución de problemas complejos de la realidad a partir de formas de pensar y actitudes sui generis, asociadas a la necesidad de comunicarse, cotejar y evaluar aportaciones, integrar datos, plantear preguntas, distinguir lo necesario de lo inútil, buscar marcos integradores, interactuar con hechos, validar supuestos y extraer conclusiones. Reconocer que la complejidad surge de la misma situación o problemática por resolver, no tiene que ver con el grado de dificultad del conocimiento, por lo cual, si se quiere hacer un diseño interdisciplinario, no se pensaría que, por ser difícil, ya se trabaja de esta forma. Incluso la complejidad toma en cuenta lo que conocen los estudiantes. Dicha complejidad está pensada desde una mirada en la que no sólo el discurso de un área específica permita explicar el fenómeno, sino que tendrán que intervenir otras áreas para poder comprender el comportamiento o solución.

Referido a un diseño interdisciplinario, Williams et al. (2016) mencionan que no debe ser limitados y que podría incluir otras disciplinas del currículo pero que depende del conocimiento y la afinidad del maestro.

Teniendo como antecedentes estas posturas sobre la interdisciplinariedad, consideramos una situación interdisciplinaria como una “secuencia de actividades que permite llegar a la construcción de un modelo, en donde el discurso matemático se relaciona con discursos extramatemáticos” (Santiago, 2023, p. 33). Dentro de los discursos extramatemáticos se relacionan otros saberes, en este caso los saberes de biología y química, generando a su vez la interdisciplinariedad escolar como forma de interacción entre las tres disciplinas elegidas en el diseño de la situación.

Por otra parte, un importante marco de referencia para la construcción y el análisis de la secuencia implementada en este estudio ha sido la modelación matemática, referida al proceso de utilizar las matemáticas para resolver problemas del mundo real (Niss, Blum y Galbraith, 2007). De acuerdo con Maaß (2010), un modelo es una representación simplificada de la realidad, y como mencionan Eck, Garcke y Knabner (2017), la modelación matemática relaciona un problema específico de las ciencias naturales, de las ciencias sociales o de la tecnología con un problema matemático. Sin embargo, aunque muchos investigadores están de acuerdo en que los modelos matemáticos deben integrarse en las aulas de matemáticas, no se ha desarrollado una conceptualización cohesiva de cómo se puede y se debe hacer (Kaiser y Sriraman, 2006).

La modelación es un proceso que permite la articulación entre el modelo y lo modelado, con lo cual los elementos de un sistema se piensan como elementos en otro sistema (Lesh y Caylor, 2007).

En las ciencias exactas y ciencias naturales los sistemas conceptuales que los humanos desarrollan para dar sentido a sus experiencias generalmente se denominan modelos. Una noción primaria de los modelos es que son sistemas familiares que se están utilizando para dar sentido a otros sistemas menos familiares, para algún propósito. Por ejemplo, una ecuación algebraica puede representar un fenómeno de la física, pero a veces no se requiere de expresiones algebraicas para modelar, a veces una tabla o una figura, también son la explicación de un sistema extramatemático (Lesh y Sriraman, 2005).

Consideramos que cuando se realiza investigación didáctica relacionada con la modelación matemática es necesario posicionarse en una de las cinco perspectivas de modelación propuestas por Abassian et al. (2019): la educativa, la realista, la sociocrítica, la epistemológica y la contextual. Esta investigación se inscribe en la perspectiva contextual, antes llamada perspectiva de obtención de modelos por Kaiser y Sriraman (2006), en la cual se entienden los modelos como:

sistemas conceptuales que consisten en elementos, relaciones, operaciones y reglas que gobiernan las interacciones que se expresan utilizando sistemas de notación externos y que se utilizan para construir, describir o explicar los comportamientos de otros sistemas, tal vez para que el otro sistema se puede manipular o predecir de forma inteligente [Lesh y Doerr, 2003, p. 10].

Esta definición hace referencia a que un modelo matemático es una herramienta conceptual de un sistema matemático que se desarrolla a partir de una situación específica del mundo real (Lesh et al., 2003) y visto como sistema, está compuesto por diferentes conceptos, que mapean diferentes características de sistemas relacionados.

A partir de la perspectiva contextual de la modelación matemática, seleccionada para realizar la situación interdisciplinaria de este estudio, existen algunas actividades de modelación o tareas que delinean cómo las y los estudiantes llegan a un modelo matemático. Una de las actividades son las Model-Eliciting Activities (mea), las cuales son definidas como “aquellas que permiten que los sujetos inventen y prueben modelos, con el fin de desafiarlos a construir modelos para resolver problemas complejos del mundo real, interpretándose así como una oportunidad de aprendizaje en la que se crea un modelo a lo largo de una secuencia de aprendizaje” (Doerr y Lesh, 2011, p. 250). Cada actividad solicita a los estudiantes que interpreten matemáticamente una situación compleja del mundo real y requiere la formación de una descripción matemática, procedimiento o método con el fin de tomar una decisión para un sujeto o situación real.

A diferencia de una actividad de matemáticas tradicional, las mea pretenden que los sujetos produzcan una descripción, procedimiento o método, en lugar de una respuesta de una palabra o un número, como sucede en otras interacciones como la resolución de ejercicios matemáticos; las soluciones de los estudiantes a la tarea revelan explícitamente cómo piensan sobre la situación dada, lo que permite ir construyendo argumentos matemáticos y extramatemáticos que posibilitan formar una red conceptual compleja (Doerr y Lesh, 2011).

Se espera que, a lo largo del proceso de modelación, los modeladores modifiquen y reinterpreten sus modelos a través de varios caminos y con base en lo que van construyendo de la red conceptual de los saberes matemáticos y extramatemáticos. En estos ciclos iterativos de reconstrucción de ideas, las y los estudiantes deben expresar sus inquietudes o pensamientos, deben probar, revisar y modificar, por lo que se convierte en un ejercicio de autoevaluación constante para solucionar el problema mediante el modelo matemático.

De acuerdo con English (2009) y Lesh y Caylor (2007), se retoman los seis principios de modelación de una mea para el diseño de la situación interdisciplinaria, los cuales son:

1. Principio de significado personal: tiene que ver con que la situación adquiera significado en la vida de las y los alumnos.
2. Principio de prototipo efectivo: que los modeladores identifiquen los saberes o las actividades más efectivas para construir el modelo.
3. Principio de construcción del modelo: que las y los estudiantes construyan diversos modelos dependiendo de la situación o con base en la construcción de saberes que van generando.
4. Principio de generalización del modelo: está relacionado con que los sujetos comprendan que el proceso de modelación o modelo aplica para otras personas o situaciones.
5. Principio de autoevaluación: este principio está relacionado con los momentos en los cuales los estudiantes se cuestionan si sus modelos cumplen o no con la solución del problema. Muchas veces la intervención docente es la que lleva al grupo a pensar de esta forma.
6. Principio de documentación del modelo: se refiere a que el grupo externalice su forma de pensar, logrando que el razonamiento sea compartido, para que entre la escucha activa y el diálogo constante se vayan construyendo los modelos.

Metodología

Este estudio tuvo como objetivo diseñar una situación interdisciplinaria; basada en la modelación matemática desde la perspectiva contextual y retomando los principios de modelación de una mea. Se trató de una situación de nutrición cuyo objetivo fue construir menús saludables con base en las características de una dieta correcta. Con base en lo que Lesh y Doerr (2003) definen por modelo matemático, los modelos obtenidos en este estudio se refieren a la construcción de menús saludables por parte de los y las estudiantes.

El diseño de investigación visibilizó el reto didáctico que tiene el colectivo docente de telesecundaria ante la premura de diseñar situaciones interdisciplinarias, tal como lo proyectan los programas de estudio 2022. Se trata de un estudio cualitativo de alcance descriptivo, del cual se obtienen como resultados modelos que construyeron los estudiantes.

Las fases que dieron estructura y orientación a la investigación fueron cuatro: diseño, pilotaje del diseño, rediseño y modelo de análisis de resultados. En la fase de diseño se delimitaron cuatro momentos que permitieron que se cumpliera con el objetivo general de investigación, es decir, el de diseñar la situación interdisciplinaria.

Primer momento del diseño de la situación interdisciplinaria: definición de un problema real del contexto de los alumnos

Se optó por abordar una problemática particular en el contexto de la población de estudio. Se observó que en el contexto rural donde se ubicaba la escuela los alumnos consumían productos poco nutritivos durante el receso y en ocasiones consumían menos calorías de las requeridas, lo que provoca dos escenarios en la población: desnutrición y obesidad, cuando su dieta era desequilibrada. En consecuencia, se optó por un tópico que tuviera relación con la alimentación de las y los adolescentes. Además, es en esta etapa donde surgen dudas acerca del consumo que realizan, son susceptibles a los estereotipos de cuerpo perfecto basado en la desinformación, asimismo se consideró como un tema importante para la prevención de trastornos alimenticios y enfermedades cardiovasculares.

El docente del grupo identificó las problemáticas anteriores, por lo que delimitó la temática a la de la alimentación, la cual debía cumplir con la característica de que se pudiera hacer un abordaje interdisciplinario, en el sentido de que fuera un problema complejo y que explicara el fenómeno en más de un discurso disciplinar. Por lo tanto, se decidió que la situación interdisciplinaria llevara a los estudiantes a crear menús saludables para alguno de ellos, basándose en las características de una dieta correcta: variada, suficiente, completa, equilibrada, inocua y adecuada.

Segundo momento del diseño de la situación interdisciplinaria: identificación de discursos (matemático y extramatemático)

Se identificaron los discursos, matemático y extramatemático, que pudieran vincularse para la solución del problema real. Para ello se consultaron los aprendizajes esperados y los contenidos del programa de estudios 2011 (sep, 2011a, sep, 2011b) y 2017 (sep, 2017b; sep, 2017c) de las asignaturas de matemáticas, biología y química (véase la figura 1). Nótese que hay contenidos y aprendizajes esperados que se repiten: en ciencias, las características de la dieta correcta; en química, el aporte calórico de los alimentos; en matemáticas, el cálculo de porcentajes y la proporcionalidad. Esto indica que tanto en el programa de estudios 2011 como en el 2017 hay contenidos que continúan enseñándose y que es importante incluirlos a pesar del cambio de los planes de estudio.

Figura 1. Selección de contenidos para la situación interdisciplinar

Discurso	Extramatemático		Matemático
Asignatura o disciplina escolar	Ciencias, énfasis en biología	Ciencias, énfasis en química	Matemáticas
Programa de estudios 2011	- Relación entre la nutrición y el funcionamiento integral del cuerpo humano (SEP, 2011a, p. 43). - Reconocimiento de la importancia de la dieta correcta y el consumo de agua potable simple para mantener la salud (SEP, 2011a, p. 43) - Características de una dieta correcta (SEP, 2011a, p. 43). - ¿Cómo puedo producir mis alimentos para lograr una dieta correcta aprovechando los recursos, conocimientos y costumbres del lugar donde vivo?	- ¿De dónde obtiene la energía el cuerpo humano? (SEP, 2011a, p. 69). - La caloría como unidad de medida de la energía (SEP, 2011a, p. 69). - Toma de decisiones relacionadas con: los alimentos y su aporte calórico (SEP, 2011a, p. 69). - Toma de decisiones relacionadas con: la importancia de una dieta correcta (SEP, 2011a, p. 70).	- Resuelve problemas que implican el cálculo de porcentajes (SEP, 2011b, p. 39). - Resuelve problemas de proporcionalidad directa mediante tablas (SEP, 2011b, p. 42).
Programa de estudios 2017	- Explica cómo evitar el sobrepeso y la obesidad con base en las características de la dieta correcta y las necesidades energéticas en la adolescencia (SEP, 2017a, p. 177)	- Identifica componentes químicos importantes (carbohidratos, lipidos, proteínas, ADN) que participan en la estructura y las funciones del cuerpo humano (SEP, 2017a, p. 177) - Analiza el aporte calórico de diferentes tipos de alimentos y utiliza los resultados de su análisis para evaluar su dieta personal y la de su familia) (SEP 2017a p. 177)	- Calcula valores faltantes en problemas de proporcionalidad directa (incluyendo tablas de variación). (SEP, 2017a, p. 178). - Recolectar, registrar y leer datos estadísticos en gráficas circulares (SEP, 2017b, p. 178). - Resolver problemas de cálculo de porcentajes (SEP, 2017b, p. 178).

Tercer momento del diseño de la situación interdisciplinaria: documentación del tema

Se realizó una búsqueda y recopilación de información acerca del tema de la alimentación, desde el tratamiento didáctico que hace cada disciplina escolar con dicho tópico. Para lograr este paso se analizaron los libros de texto de telesecundaria y otros libros disponibles en el catálogo de libros de texto gratuitos de la Conaliteg (Comisión Nacional de Libros de Texto Gratuitos de México) con miras a crear un cuadernillo de trabajo para los y las estudiantes.

Cuarto momento del diseño de la situación interdisciplinaria: Organización de la situación interdisciplinar

Se diseñaron 6 situaciones con el objetivo de vincular contenidos de biología, matemáticas y química. Como se puede ver en la figura 2, se planteó una situación inicial (“Situación 0. ¿Qué comí y bebí?”) en la que las y los estudiantes registraban durante cinco días lo que consumieron. A partir de ahí se centraban en conocer el funcionamiento del aparato digestivo y analizaban si sus hábitos se consideraban sanos. Después hacían el cálculo de calorías y resolvían situaciones de equivalencia de ciertos alimentos. Finalmente, desarrollaban el menú saludable.

Esta primera organización de las situaciones implicó la organización de los contenidos por asignatura y sus posibles relaciones.

Después del diseño se realizó el pilotaje. Con el cuadernillo de trabajo se realizó una intervención didáctica con un grupo de tercer grado de telesecundaria en una comunidad rural del estado de Querétaro. Cuando se terminó con la implementación, se analizaron las respuestas de las y los adolescentes²² y se identificó que las intervenciones del docente del grupo limitaron las respuestas de los alumnos ante las actividades presentadas. Así, se procedió a una fase de rediseño de la situación interdisciplinar la cual pasó de 9 a 12 sesiones, organizadas a su vez en cuatro situaciones, las cuales se fundamentaron en los seis principios de modelación de una mea (véase la figura 3 y consúltese el anexo).

Figura 2. Organización de la situación interdisciplinaria para la fase del pilotaje

Situaciones	0. ¿Qué comí y bebí?	1. ¿Qué pasa con lo que ingiero?	2. ¿Qué tan sana(o) soy?				3. ¿Cuánto es “mucho” o “poco”?	4. ¿Es lo mismo comer “x” que “y”?		5. Hagamos un menú saludable
Sesiones		1. Para empezar	2. ¿Cómo sé que mi dieta es correcta?	3. ¿Estoy normal, con bajo peso o con sobrepeso?	4. ¿Qué es lo que más consumimos durante una semana?		5. Cálculo de calorías necesarias	6. Composición química de los alimentos	7. Alimentos equivalentes	8. Propongan un menú saludable con base en las características de una dieta correcta
Disciplinas	Biología			Matemáticas y biología	Matemáticas		Química y matemáticas	Química	Química y matemáticas	Química, biología y matemáticas
Contenidos	- Registro de hábitos alimenticios	- El aparato digestivo - Registro de: sexo, edad, peso, altura y actividad física	Características de una dieta correcta	- El Plato del Bien Comer - Cálculo del índice de masa corporal (IMC) - Construcción del modelo 1: Dieta variada	- Recolectar y registrar datos en gráficas circulares		- La caloría como unidad de medida de la energía - Cálculo del índice metabólico basal (BMR)	- Los alimentos y su aporte calórico - Macronutrientes —carbohidratos, proteínas y lípidos—	Cálculo de porcentajes - Estimación de calorías por macronutriente	- Construcción del modelo 2: Dieta correcta

Figura 3. Organización de la situación interdisciplinaria para la fase de “rediseño”

Situaciones

¿Cómo están mis hábitos almentarios?

¿Cuánto es “mucho” o “poco”?

¿Es lo mismo comer “x” que “y”?

Hagamos un menú saludable

12 Sesiones

¿Qué comí y bebí?

¿Cómo están y mis hábitos?

¿Mi dieta es correcta?

¿Mucho, poco o suficiente?

¿Qué es lo que más consumimos durante la semana

La caloría como unidad de medida

Cálculo de calorías necesarias

¿En qué usa mi organismo los nutrientes

Calculemos el aporte nutrimental de nuestro menú

Analicemos un caso

Diseñemos un menú

Evaluemos el menú

Tareas

Registros de alimentación por cinco días

Recuperación de conocimientos previos a partir de la lectura de una situación de introducción al problema

Identificación de las características de una dieta correcta a través de una lectura

Relación entre una dieta variada y el Plato del Bien Comer. Identificación de variables

Análisis de la dieta que registraron durante cinco días

Definición de caloría (experimento y lectura)

Relación entre una dieta suficiente y el cálculo del BMR

Funcionamiento del aparato digestivo y los nutrientes. Dieta completa

Relación entre una dieta equilibrada y el cálculo de porcentajes de nutrientes

Comparación entre dos dietas mediante las características de una dieta correcta

Elaboración de un menú saludable a partir de las características de una dieta correcta

Coevaluación de los menús

Interdisciplinariedad

B: Registro personal de alimentos

B: Características de una dieta correcta

B: Reflexión sobre los propios hábitos alimenticios. - Análisis de datos: estadística: Recolecta, registra y lee datos en gráficas circulares (1o)

B: Necesidades energéticas en la adolescencia Q (2011): La cantidad de energía se mide en calorías

Q: Aporte calórico de alimentos. Estimar aporte calórico incluido en la dieta (de acuerdo con sexo, edad, eficiencia, etc.). B: Requerimientos energéticos de acuerdo con la actividad física

BQ: Composición química de alimentos. Organizador gráfico de biomoléculas (funciones en el organismo). B (2011): Proceso general de transformación y aprovechamiento de los alimentos. Argumenta por qué es importante una dieta correcta y agua simple

Q: Opciones de alimentos que favorezcan la dieta correcta

B: Proponer menú saludable con base en dieta correcta. M: Cálculo de porcentajes. Q: Aporte calórico de alimentos

B: Proponer menú saludable con base en dieta correcta. M: Cálculo de porcentajes. Q: Aporte calórico de alimentos

De la figura 2 a la figura 3 se puede notar un cambio en cuanto a la presentación de la información: las filas cambian de nombre pues en vez de contenidos se modifica a tareas, ya que fueron actividades que se contemplaron para el cuadernillo (anexo). Lo mismo sucedió en la fila de disciplinas, que cambió por interdisciplinariedad, con el fin de que se hiciera visible la interacción entre asignaturas. En la figura 3, la nomenclatura que se enuncia en la fila de interdisciplinariedad corresponde a la letra inicial de la disciplina por tratar; una B para biología, una M para matemáticas y una Q para química. Además, se favoreció que la construcción de los modelos matemáticos —menús saludables— no fuera una meta hacia el final de la situación, sino que, las y los estudiantes tuvieron distintas oportunidades para construir o modificar los modelos realizados, basándose en las características de una dieta correcta.

La intervención didáctica se llevó a cabo en los meses de febrero y marzo de 2019 en un grupo de 24 estudiantes que cursaban tercer grado en una telesecundaria rural. Las y los estudiantes se organizaron en seis grupos heterogéneos, con cuatro integrantes cada uno, con la finalidad de trabajar en grupos colaborativos. Las edades oscilaban entre los catorce y los dieciséis años y eran habitantes de la comunidad de La Laborcilla, El Marqués, Querétaro, ubicada a 50 kilómetros de la ciudad de Querétaro, de los cuales un tercio es un tramo de terracería, lo que imposibilita que los habitantes salgan de su comunidad con regularidad. Otra característica es que hay más habitantes mujeres que hombres, ya que estos últimos salen a trabajar a Estados Unidos, pues consideran que tienen más oportunidades de trabajo en aquel país, por lo que se acostumbra que les envíen dinero a sus esposas mientras ellas se hacen cargo de las labores domésticas y el cuidado de las niñas y niños. Un fenómeno entre las y los estudiantes que concluyen sus estudios de telesecundaria es que no dan continuidad a sus estudios de nivel medio superior. De acuerdo con relatos recuperados de los estudiantes y los docentes de la telesecundaria, esto puede deberse a que el bachillerato más cercano se encuentra a 20 kilómetros, y es limitado el traslado de los estudiantes. También, algunos adolescentes hombres proyectan que se irán a trabajar a Estados Unidos para alcanzar a sus papás y así apoyar con el gasto doméstico, mientras que algunas adolescentes mujeres ayudan con el cuidado de sus hermanos menores para educarlos y cuidarlos.

La recopilación de datos se realizó por medio de observación participante y la grabación en video y audio de las sesiones de la intervención didáctica.

Resultados

El análisis de los datos se realizó con base en los seis principios expuestos por English (2009) y Lesh y Caylor (2007): principio de significado personal, prototipo efectivo, generalización, construcción del modelo, autoevaluación y documentación del producto. Se presentan a continuación los resultados relacionados sólo con el principio de construcción del modelo, evidenciando algunos modelos que construyeron las y los estudiantes.

Los menús saludables —construcción de modelos matemáticos en el sentido de Lesh y Doerr, 2003— se construyeron en el orden en que se conceptualizaron las seis características de una dieta correcta —variada, suficiente, completa, equilibrada, inocua y adecuada—. Las características de dieta inocua y dieta adecuada no se presentarán como evidencia en la construcción de modelos, debido a que por definición una dieta inocua se refiere a que los alimentos estén libres de microbios, lo que se relaciona con la elaboración de las comidas y no con la construcción de modelos; la dieta adecuada se relaciona con los gustos alimenticios de la persona, es decir, que las comidas que contenga el menú sean del agrado y asequibles para el consumidor. Para el análisis se presentarán los modelos construidos con base en las características de dieta variada, dieta suficiente, dieta completa y dieta equilibrada.

Modelo basado en diversos alimentos – dieta variada

Para construir este modelo, las y los estudiantes analizaron el plato del bien comer, pues una dieta variada se refiere a que las personas deben consumir alimentos de los tres grupos —frutas y verduras, cereales, leguminosas y alimentos de origen animal—. La consigna para que los grupos pequeños heterogéneos diseñaran su modelo fue: Para terminar la sesión de hoy, elabora un menú saludable para un compañero con tres momentos de alimentación (desayuno, comida y cena)”. Un ejemplo de lo que realizaron los estudiantes se observa en la figura 4, el modelo muestra un registro de 3 alimentos del grupo de frutas y verduras, 4 alimentos del grupo de cereales y 4 del grupo de origen animal y leguminosas.

Se observa que para algunos alimentos sí se coloca la ración que se va a consumir, por ejemplo: menciona que consumirán 1 licuado, 3 tortillas, 1 vaso de leche, 1 manzana y 5 galletas. Sin embargo, para otros alimentos los estudiantes no consideran importante colocar la cantidad, como en el caso de la fresa, el huevo, el arroz y la carne. Esto muestra que, si el menú quedara solamente así, cumpliendo con la característica de variada, la dieta no sería completa. Por definición, la característica de que la dieta sea variada es que la dieta contenga diversos alimentos incluidos en el plato del bien comer, la cantidad de alimentos y las raciones se incorporaron posteriormente.

Modelo basado en el cálculo de calorías – dieta suficiente

Previamente los estudiantes elaboraron un menú sin tomar en cuenta las cantidades o porciones de cada alimento, sólo se fijaron en si contaban con diversos alimentos; para este segundo momento sabían que cada persona requiere energía para realizar sus actividades diarias, asimismo calcularon cuántas calorías necesitan diariamente por medio de la fórmula del índice metabólico basal (bmr),²³ y tenían que decidir si el menú que estaban elaborando correspondía a las necesidades energéticas de la persona a quien le elaboraban el menú.

Los modelos construidos por el equipo 4 ejemplifican la modificación del modelo anterior a uno nuevo que contempla las raciones y el aporte calórico de cada alimento. Arturo, integrante del equipo, muestra el menú que realizó en la sesión anterior (véase la figura 5), y con base en lo aprendido, modifica junto con su equipo el menú saludable (véase la figura 6).

En este segundo momento el equipo tomó en cuenta elementos no previstos anteriormente, incluso agregaron dos momentos más de alimentación que nombraron como almuerzo y merienda. Para determinar el número de calorías que aporta cada alimento, lo que hicieron fue basarse de un material con el que cada equipo contaba llamado Guía de alimentos para la población mexicana, en el cual se encuentra un listado de alimentos que está organizado por grupo y cada uno tiene un compendio de alimentos que toma en cuenta la ración, la energía calórica que aporta y los macronutrientes medidos en gramos. El equipo lo usó para elegir alimentos como el cereal de caja con azúcar, registrado en el desayuno, y calculó cuántas calorías aporta dicho alimento, en este caso 210 cal. Este equipo representa con una k las calorías que calculan.

Pasar de un modelo a otro también cumple con el principio de auto­evaluación que mencionan Lesh y Caylor (2007), ya que fue necesario que el equipo reflexionara sobre si su modelo estaba terminado o qué le faltaba para cumplir con la característica de que fuera suficiente.

En este modelo fue donde recurrieron a sus saberes matemáticos para comprobar que la suma calórica de los alimentos elegidos cumplía con las necesidades energéticas de la persona a quien le hacían el menú. Para ello, se puede observar en la parte inferior de la figura 6 que escriben k = 897, lo que se interpreta como el total de calorías que se estaría consumiendo con ese menú. La suma la obtuvieron de la siguiente forma: primero, pusieron las calorías de los alimentos en la parte inferior de su menú y las etiquetaron con una k; una vez que terminaron de colocar todos los alimentos, se fijaron en los números de la parte inferior y sumaron lo siguiente (figura 7):

Figura 7. Cálculo de la suma de calorías del modelo de Arturo, equipo 4

Desayuno	Almuerzo	Comida	Cena	Merienda
210 k + 95 k + 95 k +	70 k + 40 k +	200 k + 40 k + 75 k +	7 g + 40 k + 25 k	No lo tomaron en cuenta en la suma

El haber omitido la merienda, así como otros alimentos, los llevó a obtener ese resultado; sin embargo, de acuerdo con la Guía de alimentación para la población mexicana debió haber sido de 1057.5 calorías.

Ante la tarea de determinar si el aporte calórico del menú que diseñaron corresponde a las necesidades energéticas de la persona a quien se lo esbozaron (calculando el bmr para dicha persona), el equipo respondió que sí corresponde porque el menú contiene diversos alimentos del plato del bien comer, pero que le faltan 338.45 calorías al menú para cubrir las 1235.4 calorías que requiere el alumno a quien le hicieron el modelo. Ese faltante lo determinan a través de una resta (figura 8):

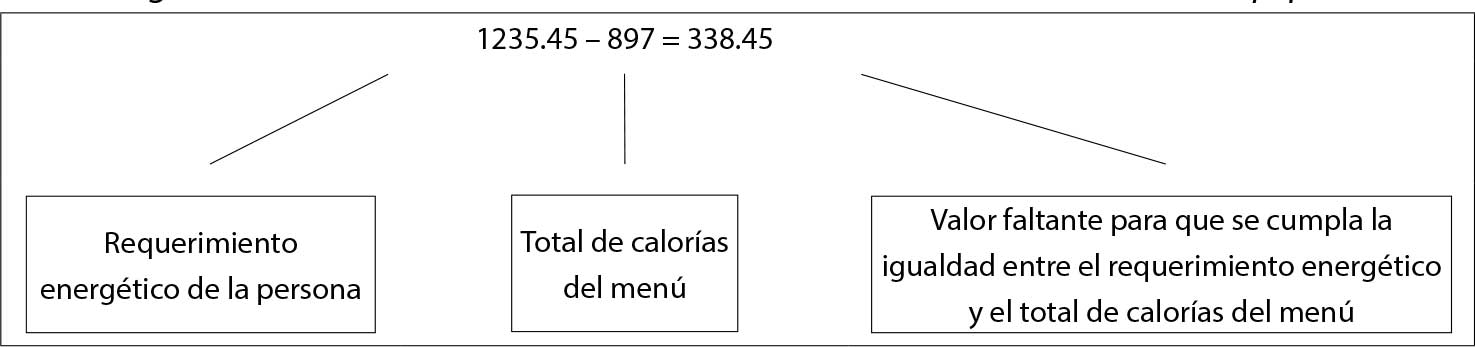
En conclusión, este modelo permitió que las y los estudiantes modificaran sus modelos y argumentaran con cálculos matemáticos si se cumplía o no con la característica de que la dieta que fuera suficiente.

Modelo basado en la identificación de macronutrientes – dieta completa

Como siguiente paso del proceso de modelación pensaron qué alimentos son más nutritivos que otros ya que, si se trata sólo de cubrir cierta cantidad de energía, entonces cualquier producto puede aportar al total de calorías. En el modelo de la figura 6 las y los estudiantes incluyeron alimentos al azar para algunos momentos de alimentación, por lo que debían ahora elegir aquellos que pudieran estar al alcance de la persona que consume. Asimismo, otra ruptura que debían hacer todos los alumnos era que no porque debían consumir 2000 calorías significaba que los alimentos que consumieran podrían ser de cualquier tipo, por ejemplo, que las 2000 calorías que consumieran fueran de comida chatarra, estaría mejor pensar qué alimentos tienen más nutrientes que les ayuden a su organismo para considerarse sano.

El modelo que se presenta en la figura 9 pertenece a una estudiante del equipo 3. Su menú tiene como título Menú para todo el día. Con rectángulos de color verde, morado y amarillo encierra los momentos de alimentación correspondientes a desayuno, almuerzo y cena. De igual manera, aparecen unos números a un costado de ciertos alimentos, que representan las calorías y también indican a un costado de los momentos de alimentación otra cifra que se infiere que es la suma de calorías. Hacia la derecha tiene colocado el número de macronutrientes que tiene en total su menú (véase la figura 9).

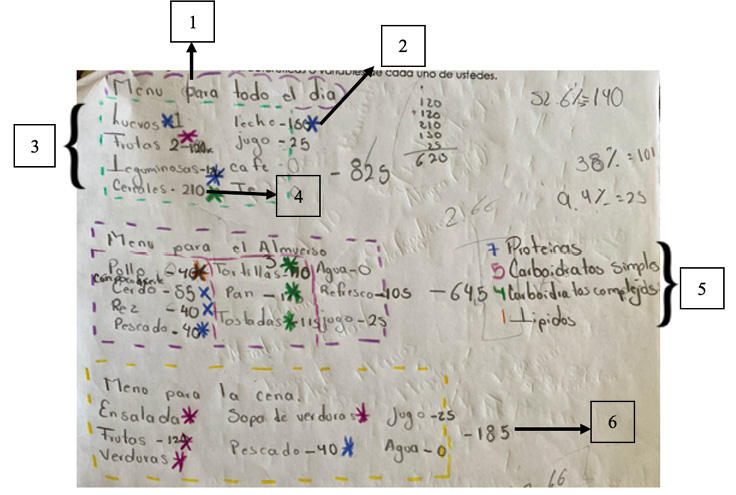
Número	Representación
1	Título del modelo
2	Asterisco de color azul indicando que la leche es una proteína
3	Momento de alimentación: desayuno
4	Calorías que tiene el cereal
5	Registro del total de macronutrientes que tiene el menú
6	Suma de calorías totales que tiene la cena

Lo que muestra Brianda es que fue relacionando los alimentos con el macronutriente que predomina en cada uno y al final indica que su menú cuenta con 7 proteínas, 5 carbohidratos simples, 4 carbohidratos complejos y 1 lípido. Ese equipo se basó en la Guía de alimentación para identificar cada macronutriente.

De este análisis se partió para obtener el siguiente modelo; para ejemplificar lo anterior se dice que los jóvenes, cuando escriben la palabra pollo en su modelo, lo indican con un asterisco azul dado que es una proteína, aunque notaron que no tenían lípidos, por lo que agregaron la leyenda con poco aceite y encimaron un asterisco de color naranja para contar al pollo como un lípido. Esto indica que ellos buscaron una forma para que su menú cumpliera con la característica de completo, es decir, que tenga los tres macronutrientes, empero este error permitió detenerse a pensar que algunos alimentos contienen lípidos, proteínas y carbohidratos al mismo tiempo, por lo que debían contemplar ese dato para su siguiente modelo.

Modelo basado en el porcentaje de macronutrientes – dieta equilibrada

Las y los estudiantes empezaron a notar que hay alimentos que contienen los tres macronutrientes, no sólo tienen uno, por lo que debían descomponer aún más los alimentos y era muy probable que el modelo que habían realizado hasta el momento no fuera suficientemente específico.

La actividad pertenece a la sesión 9 Calculemos el aporte nutrimental de nuestro menú (consúltese el anexo) consistía en generar una tabla en la que calcularan las unidades de aporte nutrimental por cada ración de alimento que incluyeron en el menú. El descomponer los alimentos en unidades les permitió saber el porcentaje de macronutrientes que contempla el modelo. Por último, compararon estos porcentajes del menú con los que se sugiere que consuma una persona: 60 % de carbohidratos, 30 % de proteínas y 10 % de lípidos (porcentajes adaptados para el diseño didáctica, de los sugeridos por la Organización Mundial de la Salud). Esta comparación les permitió determinar si su menú era equilibrado, siendo ésta otra característica indispensable que debe tener una dieta correcta.

Lucrecia, una alumna del equipo 2, inicia haciendo una tabla (véase la figura 10) en la que muestra tres momentos de alimentación (filas) y en cada uno incluye las raciones y los alimentos. Las columnas corresponden a los tres macronutrientes —carbohidratos, proteínas y grasas—, los cuales convierte en unidades, por ejemplo: 1 taza de leche contiene 5 unidades de carbohidratos, 15 unidades de proteínas y 6 unidades de grasa. Para calcular los datos de las unidades las y los estudiantes se basaron en un cuadro proporcionado en el cuadernillo.

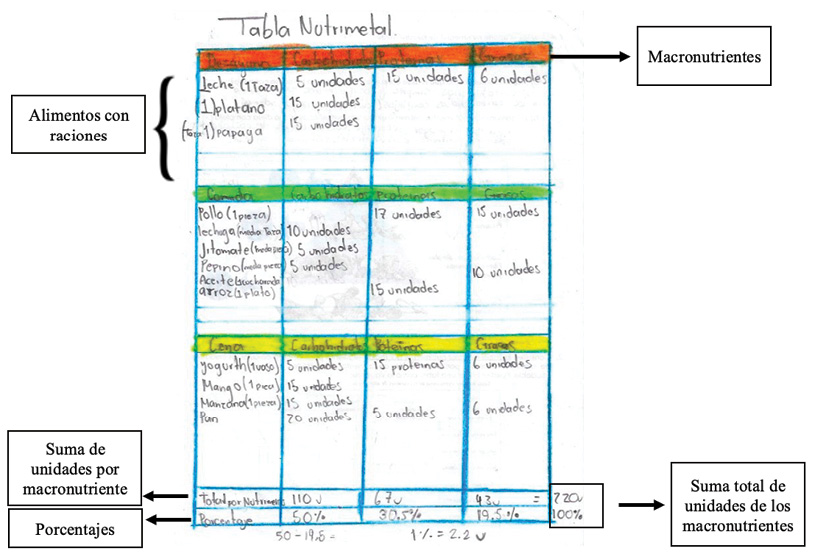
En esta actividad Lucrecia identificó varias tareas matemáticas:

• Convertir en unidades los alimentos a partir de sus raciones. Lucrecia se dio cuenta de que en el cuadro en el que se estaba apoyando cambiaban las raciones de un alimento a otro, se nota que tomó en cuenta esto porque en el jitomate pone en su modelo que sólo va a consumir ½ pieza, en el cuadro de apoyo no viene media pieza, sino 1 pieza que equivale a 10 unidades de carbohidratos, por lo que ella pone 5 unidades en carbohidratos, es decir, lo correspondiente a la mitad de la pieza.
• Suma de las unidades por cada macronutriente. Una vez que identificó las unidades por cada alimento, sumó por columnas el total de unidades que tiene cada macronutriente. Por ejemplo, con los carbohidratos la suma de unidades que hace es: 5 + 15 + 15 + 10 + 5 + 5 + 5 + 15 + 15 + 20 = 110 unidades.
• Cálculo de porcentajes por cada macronutriente. En la fila del modelo de Lucrecia que nombra como “total por nutrimento” se observa que coloca al final del lado derecho 220u, éste lo obtuvo al sumar las unidades de los macronutrientes: 110 + 67 + 43 = 220.

Ella sabía que, al tener esta suma, sería equivalente al 100 % y lo colocó debajo del número. Se nota también que escribe el valor unitario del porcentaje como 1 % = 2.2 unidades, aunque cuando el docente acude al equipo, las y los estudiantes mencionan que no saben cómo calcular los porcentajes correspondientes a las proteínas y las grasas. A partir del valor unitario el docente pregunta: “Si 1 % equivale a 2.2, ¿cuántas unidades serían por 2 %? ¿y por 3 %? ¿y por 4 %?” En ese momento Valentina responde “¡Ah, sí!” y comienza a hacer algunos cálculos en su libreta con apoyo de su calculadora (véase la figura 11).

Valentina va sumando el valor unitario reiteradas veces en su calculadora al mismo tiempo que las va registrando hasta que llega al 20 % que corresponden a 44 unidades. Es cuando se detiene, observa que en la suma de unidades de las grasas tiene 43 unidades y por ello empieza a decir: “El 43 está por aquí —señalando el 19 % y 20 % que tiene registrados en su libreta—” y les dice a sus compañeros de equipo: “Hay que ponerle 19.5 %”. Lo que ella hizo no fue calcular el porcentaje exacto sino un valor aproximado a éste. Después de que lo registran en su tabla, ya no utiliza el procedimiento de ir sumando el valor unitario, sino que Lucrecia dice: “Para el otro (refiriéndose al cálculo de porcentaje de las proteínas) sólo réstale ahí (en la calculadora) 50 − 19.5”; esto indica que Lucrecia sabía que no era necesario que al 100 % le restaran el 50 % de carbohidratos menos 19.5 % de grasas porque era más económico que no tomaran en cuenta el 50 % de carbohidratos. Asimismo, sabía que al restar 50 % menos el porcentaje de grasas obtendría el restante correspondiente a las proteínas. Por ello registran 30.5 % de proteínas.

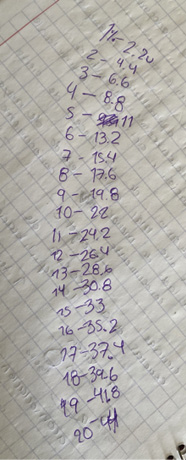
Una vez que calcularon los porcentajes, como siguiente actividad compararon los porcentajes obtenidos con los presentados en el cuadernillo (véase la tabla 1). Al compararlos debían responder si su modelo se podía considerar como equilibrado y qué podrían hacer para equilibrarlo.

Table 1. Comparación de porcentajes entre lo calculado y lo presentado en el cuadernillo.

Macronutrientes	Porcentaje presentado en el cuadernillo	Porcentaje calculado por el equipo
Carbohidratos	60 %	50 %
Proteínas	30 %	30.5 %
Grasas	10 %	19.5 %

Fuente: creación propia con base en los registros de Lucrecia.

Como se puede interpretar, el valor más aproximado a lo que se debe consumir es el del grupo de proteínas, en cuanto a los carbohidratos les faltaría consumir 10 % más y disminuir las grasas en un 9.5 %. Cuando se preguntó si lo consideraban equilibrado ellos expresaron que sí y su argumento fue que el porcentaje de proteínas y de carbohidratos se acerca y que las grasas se pasaban, en cuanto a la segunda pregunta referida a cómo podrían equilibrarla, manifestaron que podrían consumirse más alimentos que contengan carbohidratos, como frutas y verduras, y disminuir las grasas. A pesar de que los argumentos son los esperados, para que la dieta sea equilibrada falta ajustar algunos macronutrientes; no obstante, el equipo muestra indicios de cómo mejorar su modelo.

Discusión y conclusiones

Como mencionan Williams et al. (2016), los proyectos interdisciplinarios tienden a cruzar los límites tradicionales entre disciplinas académicas y forzosamente en esa relación las disciplinas deben significarse entre sí. El diseño didáctico presentado puso de manifiesto discursos de tres disciplinas en el ámbito escolar, la matemática, la química y la física. Partimos de considerar la interdisciplinariedad escolar como una manera de relacionar los discursos de las disciplinas escolares para que las y los estudiantes interactuaran con ellos y construyeran modelos matemáticos entendidos como sistemas conceptuales en los términos de Lesh y Doerr (2003).

El primer modelo relacionado con la diversificación de alimentos revela que el discurso es extramatemático, es decir, los argumentos que utilizan las y los estudiantes para dar significado al modelo se relacionan con la biología. Utilizar argumentos de una sola disciplina lo consideramos como uso de un discurso monodisciplinario. En este caso es evidente la prevalencia de los saberes de biología, ya que el que la dieta se relaciona con los grandes grupos de alimentos, sin tomar en cuenta las cantidades o porciones de cada alimento.

En el segundo modelo, de dieta suficiente, consideramos que se da una relación entre biología y matemáticas debido a que fue importante que los modeladores generaran argumentos matemáticos para justificar por qué es importante cubrir cierta cantidad de calorías en el organismo, pues dicha energía la proporcionan los alimentos que ingerimos, por lo que una manera de conectar la dieta que se consume y los requerimientos energéticos de las personas es calculando y aproximando ambos valores.

El modelo que se basaba en una dieta completa se ubica en un discurso de química debido a que se examinan los componentes de los alimentos y las y los estudiantes conocieron la función que tienen los macronutrientes en la alimentación, por lo que el análisis fue monodisciplinario.

En el modelo basado en el porcentaje de los macronutrientes, la interdisciplinariedad entre los discursos matemáticos y extramatemáticos se evidencia por el uso de procedimientos matemáticos para determinar si el modelo cumple con la función de que es nutritivo. Esta relación que hay entre el porcentaje y los alimentos es de suma importancia para el funcionamiento correcto de nuestro organismo, por lo que las disciplinas que se relacionan son tres: matemáticas para el cálculo de la composición química de los alimentos, la química que permite dar información sobre el aporte nutritivo de los alimentos y la biología que tiene el interés del buen funcionamiento del cuerpo humano a través de la alimentación como fuente de energía.

A pesar de que el diseño de la situación tiene la característica de ser interdisciplinario, hay momentos en los que predomina el discurso de una disciplina, logrando momentos de monodisciplinariedad, que consideramos necesarios para institucionalizar los conocimientos de cada disciplina.

Si bien en los tres primeros modelos había cierta interacción entre disciplinas, fue hasta el final donde las y los estudiantes generaron un conocimiento entre los tres saberes de la situación interdisciplinaria, lo cual permitió construir un conocimiento que denominaremos híbrido. Por ejemplo, en el cuarto modelo se observa que la explicación de las y los estudiantes incorpora los discursos matemáticos y extramatemáticos, lo que sería un ejemplo de conocimiento híbrido.

Pensar en materiales educativos que respondan a todos los contextos sociales sin duda se vuelve cada vez más complejo, sin embargo, que las y los docentes abandonen prácticas de enseñanza basadas únicamente en contestar los libros de texto pudiera ser una realidad. El reto de diseñar dispositivos didácticos pertinentes para telesecundaria representa un desafío para los docentes y es alentador encontrar estudios que aborden esta problemática para la enseñanza de las matemáticas (véase Ruiz-Rojas et al., 2020).

La situación interdisciplinaria que se presentó en este estudio se enmarca en el contexto de la modelación matemática. Alsina y Salgado (2022, p. 84) reconocen el auge que ha tenido en los últimos años la modelación matemática a nivel mundial, incluso mencionan que “se puede trabajar desde el preescolar o educación infantil”, todo con el fin de tener acercamientos con la matemática escolar desde situaciones prácticas en donde las y los estudiantes interactúen y transformen situaciones del mundo real y sean llevados a trabajar matemáticamente en soluciones.

Cuando hablamos de situaciones del mundo real estamos pensando en la realidad de las y los adolescentes de secundaria, pues una sugerencia didáctica de Alsina y Salgado (2022, p. 89) es que sean reales en las mentes de los niños debido a que esto “permite desarrollar una verdadera conexión de significados de los objetos matemáticos y su utilidad en la vida cotidiana”. El tema que se eligió para la situación fue de la sana alimentación, siendo un tema que interesó a las y los adolescentes desde el inicio, pues se sintieron motivados a querer saber más sobre la temática.

Una sugerencia didáctica al momento de diseñar una situación interdisciplinaria es que el tema elegido no se limite a un contexto inmediato. Las y los estudiantes tienen el derecho de recibir una educación que les permita pensar en su contexto inmediato y en el no inmediato, posibilitando que lo aprendido tenga un alcance mayor para resignificar lo aprendido. Es por ello que también hay que tomar en cuenta lo que English (2009) y Lesh y Caylor (2007) nombran como principio de generalización del modelo, ya que en la situación interdisciplinaria que se presentó en esta investigación fue importante que el modelo matemático construido pudiera ser reinterpretado hacia otras personas, pues el proceso de modelación es el que permite que pueda ser generalizable y hacer menús para otras personas.

La enseñanza interdisciplinaria desafía a las y los docentes de telesecundaria, pero se reconoce como una oportunidad que tienen debido a que son quienes están frente al grupo y pensando en todo momento en las asignaturas que imparten, lo que les da un conocimiento acerca de qué enseñar y cómo hacerlo, optimizando tiempos y diseñando sus propias situaciones. Cabe mencionar que para que se reconozca como una situación interdisciplinaria, se debe lograr un equilibrio entre las asignaturas que se elijan, esto se hace con el fin de que los discursos matemáticos y extramatemáticos tengan sentido y que a su vez se acompañen en la construcción de conocimientos complejos en los estudiantes.

---

Bibliografía