9. ¿Qué significa colaborar en el marco de un trabajo colectivo entre maestros e investigadores?
Dimensions
9. ¿Qué significa colaborar en el marco de un trabajo colectivo entre maestros e investigadores?
Yesenia Castaño Torres*
David Block Sevilla**
DOI: https://doi.org/10.52501/cc.132.09
Resumen
En este artículo analizamos las maneras concretas en que colaboraron maestros de matemáticas en servicio e investigadores en el marco de un trabajo conjunto que tuvo por objetivos la problematización, implementación y análisis de un conjunto de situaciones didácticas dirigidas a identificar y analizar características que determinan la congruencia de dos figuras en primer año de secundaria. Asimismo, se buscó ofrecer una experiencia de formación continua a los maestros respecto de la enseñanza de la geometría. La experiencia se desarrolló con cuatro maestros de dos escuelas de la Ciudad de México y tres investigadores, y tuvo una duración de cuatro semanas alternando sesiones de trabajo colectivo y la implementación de las situaciones en el aula por parte de los maestros. En este texto centraremos el análisis en las distintas maneras en que se dio la colaboración y las condiciones que favorecieron o dificultaron dicha colaboración durante la experiencia.
Palabras clave: trabajo colaborativo, formación docente, enseñanza de la geometría, educación secundaria.
Introducción
La problemática en la que se inscribe este estudio es la de la enseñanza de la geometría en la escuela secundaria. Algunas investigaciones (Itzcovich y Broitman, 2001) han reportado que este sector de las matemáticas ha ido perdiendo espacio y sentido, tanto en los programas curriculares como en la formación docente, lo que ha dificultado a los maestros el diseño, selección y/o adaptación de situaciones de enseñanza que brinden una oportunidad de formación matemática para los estudiantes (Itzcovich, 2005).
El ángulo desde el cual abordamos esta problemática es el de la formación de maestros en servicio, en particular mediante una estrategia de trabajo colaborativo entre maestros e investigadores que aporte una experiencia de formación continua respecto de la enseñanza de la geometría. En este texto nos interesa analizar el trabajo conjunto entre los distintos actores en términos de lo que para cada uno significó la colaboración.
Cuestiones teóricas
El enfoque en el que se inscribe este estudio es el modelo colaborativo de la investigación educativa propuesto por el equipo de Desgagné et al. (2001). Este enfoque es una de las alternativas que se han desarrollado en el marco de la investigación participativa (Anadón y Couture, 2007), cuyo eje central está constituido por una actividad reflexiva entre profesionales e investigadores que se reúnen para interactuar y explorar juntos un aspecto de la práctica de los primeros que sea de interés común. Esta actividad reflexiva se basa en la explicitación, la clarificación y el análisis de situaciones de enseñanza —implementadas por los profesionales— en el marco de una experiencia de trabajo colaborativo (Morellato, 2017). Se busca garantizar una especie de conversación entre la práctica de los profesionales y la retroalimentación reflexiva sobre esta práctica (Schön, 1991, en Desgagné et al., 2001). El trabajo conjunto entre los distintos actores da lugar a una perspectiva de investigación para la producción de conocimiento y una experiencia de formación continua para los profesionales (Desgagné et al., 2001). Con esto no se pretende que investigadores y maestros hagan juntos un trabajo de investigación, sino que hagan juntos un proyecto que interese a ambos, con el cual los maestros puedan tener una experiencia formativa, los investigadores puedan aportar conocimientos sobre algún aspecto que les interesa investigar, y ambos aporten conocimientos sobre las situaciones didácticas implementadas.
Se trata entonces de modificar el estatuto de “aplicadores de los productos de la investigación” que se ha atribuido a los maestros, para convertirlo en el de co-constructores de un saber del que ellos y su práctica son la fuente (Desgagné, 1997).
Por otra parte, esta forma de trabajo con los docentes ayuda a hacer frente a una problemática particular de la investigación en didáctica relacionada con el tema de la reproducibilidad de las situaciones didácticas en los contextos escolares. A lo largo del tiempo se observó que a los maestros les resultaba difícil replicar las situaciones diseñadas en el ámbito de la investigación y, al adaptarlas a su forma de hacer las cosas, frecuentemente las alejaban de los objetivos que se habían planteado los investigadores (Bednarz et al., 2001). Se fue comprendiendo que las situaciones didácticas que los maestros utilizan para impartir sus clases son objeto de apropiación por parte de ellos de acuerdo con las condiciones institucionales, sus concepciones sobre la enseñanza y el aprendizaje, entre otras. El modelo colaborativo en el que se inscribe este estudio aborda el tema de la producción de secuencias didácticas para la práctica docente desde otra perspectiva: se concibe que tal producción debe considerar el punto de vista de los profesionales, su conocimiento de la experiencia, su contexto particular y sus rutinas de intervención, entre otras (Bednarz et al., 2001).
Cuestiones metodológicas
El enfoque colaborativo adoptado para este estudio (Desgagné et al., 2001) destaca tres etapas en la colaboración entre investigadores y maestros en los diferentes momentos de la investigación: la cosituación, la cooperación y la coproducción. En la definición de estas etapas se respetan las lógicas con las que se vincularon los distintos actores (Desgagné et al., 2001). A continuación precisamos en qué consistieron estas etapas.
La cosituación
En este primer momento se define el objeto de interés común entre los maestros y los investigadores de manera que satisfaga los intereses y las preocupaciones de ambos. Se trata de ofrecer una forma de desarrollo profesional para los docentes; una producción de conocimientos sobre la experiencia de trabajo conjunto por los investigadores, y un conocimiento sobre el funcionamiento de las situaciones en el aula y su factibilidad por ambos. En este estudio la iniciativa nació de los investigadores en el marco de una tesis de maestría13 (Castaño, 2021), con miras a brindar una experiencia que abone a la formación continua de los maestros acerca de la enseñanza de algunos aspectos de geometría, bajo un enfoque didáctico específico.
Desde el inicio, los investigadores sometieron a consideración de los docentes el tema (geometría) y tres situaciones didácticas, incluyendo una descripción de las distintas fases que las componen. Cabe advertir que en este punto optamos por un camino distinto al de otros trabajos colaborativos (véase, por ejemplo, Sadovsky et al., 2019) en los que todas las decisiones, incluso la selección de las situaciones mismas, se toman en conjunto entre los maestros y los investigadores. En nuestro caso, recuperamos situaciones producidas en la esfera de la investigación, con cualidades didácticas potenciales14, y las ponemos a consideración con la idea de que, si resultan de interés para los maestros, ellos les imprimirán su sello y las adaptarán, si no desde la planeación, ciertamente al implementarlas en sus aulas. Esto fue ampliamente corroborado en el desarrollo de esta experiencia.
Los docentes, los estudiantes, los investigadores. Participaron de forma voluntaria cuatro maestros de matemáticas de secundaria de dos escuelas oficiales de la Ciudad de México: Liliana e Ignacio de una secundaria general, y Sara y Fabio de una secundaria técnica15. En las dos escuelas los grupos tenían en promedio 40 estudiantes y sus edades oscilaban entre los 13 y los 15 años. El equipo de investigadores estaba conformado por un investigador experimentado en didáctica de las matemáticas, una maestra en didáctica con amplia experiencia y una investigadora en formación.
Los contenidos, las situaciones. Los contenidos geométricos elegidos fueron la construcción de triángulos y cuadriláteros, así como los criterios de congruencia de triángulos, ambos ubicados en los aprendizajes esperados en primer año de secundaria del programa oficial (sep, 2017). Las situaciones elegidas, tipificadas como “de comunicación”, se caracterizan en el marco de la teoría de las situaciones didácticas (tsd) por la necesidad de comunicar, a través de un mensaje escrito, información que el receptor de la comunicación necesita para llevar a cabo determinada tarea, en este caso, reproducir una figura (Brousseau, 1998). Dicha información involucra los conocimientos que se espera que los estudiantes adquieran. Como investigadores, nos interesó llevar a los docentes una propuesta de enseñanza que de entrada ofreciera condiciones favorables para que los estudiantes superaran una “mirada perceptiva” (Duval, 2016) sobre las figuras y comenzaran a buscar los elementos y las relaciones que las definen. Esta elección se dio con base en un análisis previo de las situaciones, en el sentido de la ingeniería didáctica (Artigue, 1995), el cual incluyó un estudio desde la disciplina del contenido geométrico y una revisión de investigaciones didácticas sobre el tema, entre las que cabe destacar los estudios realizados por Fregona (1995).
Las situaciones de comunicación se realizan con una dinámica parecida a la de un juego: se organizan equipos conformados, cada uno, por uno o dos emisores y uno o dos receptores. Los emisores tienen un dibujo de una figura y los receptores deben reproducir esa figura, sin verla. Para ello, los emisores deben enviar un mensaje escrito a los receptores. Ganan los equipos que logren reproducir las figuras de manera idéntica. Así, los emisores y receptores no compiten entre sí, se da lugar a un trabajo cooperativo entre ellos, al interior de cada equipo. La validación se hace por superposición de la copia con el dibujo original. Para este estudio optamos por tres figuras geométricas, y organizamos una situación para cada una. La primera consistió en reproducir configuraciones hechas con base en rectángulos, con alguna diagonal o línea paralela a uno de sus lados; se esperaba que esto fuera relativamente sencillo para los estudiantes y buscaba servir de introducción al juego de comunicación, a sus reglas, su meta y su funcionamiento. La segunda situación involucraba la reproducción de un paralelogramo y la tercera, la reproducción de un triángulo. Advertimos que la construcción del triángulo podía ser más accesible para los estudiantes que la del paralelogramo, considerando que con el primero podían evitar la descripción de los ángulos, mientras que con el segundo, para evitar la información de los ángulos, era necesario usar la altura o la diagonal. Sin embargo, a la situación de reproducir triángulos le asignamos también la función de poner en juego los criterios de congruencia de triángulos, razón por la cual quedó en tercer lugar.
Para cada una de las situaciones didácticas que propusimos, ofrecimos una ficha didáctica a los docentes con los objetivos para los estudiantes, los tiempos y materiales, así como algunas sugerencias generales para la gestión en aula —puestas en común e institucionalización— y anticipaciones sobre las posibles producciones de los estudiantes. Aunque la información fue amplia, dejamos fuera varias precisiones sobre condiciones que se podrían requerir para hacerlas funcionar, que consideramos que los maestros podrían determinar. La razón de esta decisión fue no saturarlos de entrada con información, provocando la sensación de una situación rígida y difícil de poner en práctica. Como se verá más adelante, los maestros imprimieron importantes adaptaciones personales a las situaciones a la hora de llevarlas al aula.
El dispositivo de formación. Con el término dispositivo nos referimos a las condiciones de trabajo que establecimos para favorecer un proceso de colaboración entre investigadores y maestros, y más específicamente, a la dinámica de alternancia entre las sesiones colectivas y las implementaciones de las situaciones por parte de los docentes. A lo largo de cuatro semanas se tuvo una sesión colectiva semanal y la implementación de una situación. Las sesiones se realizaron en una de las escuelas, lo que implicó para los docentes de la otra escuela tener que asistir fuera de su tiempo de trabajo. Los docentes anfitriones fueron remplazados en sus clases por otros de sus colegas durante el desarrollo de las sesiones. La duración de cada sesión fue de 120 minutos.
Las sesiones con los maestros fueron videograbadas y tuvieron dos propósitos centrales: 1) planear las clases siguientes y 2) analizar sus clases en aula. Mencionamos a continuación lo que nos interesaba con cada uno de estos espacios.
1) La planeación. Se buscó enriquecer el trabajo de planeación que habitualmente hacen los maestros antes de ir a las aulas. Se trataba de construir una intención didáctica común en torno a cada una de las situaciones que se implementarían sin aspirar con ello a implementaciones homogéneas, pues se consideró que serían objeto de una apropiación por parte de los docentes de acuerdo con sus condiciones institucionales y sus concepciones con respecto a los conceptos enseñados y el aprendizaje. Como investigadores nos interesaban dos asuntos: i) destacar las condiciones de implementación necesarias para que las situaciones pudieran funcionar, por ejemplo, la necesidad de que los estudiantes contaran con regla graduada, compás y transportador o que los emisores no vieran la figura de los receptores; y ii) que los cambios imprimidos por los docentes a las situaciones tuvieran en cuenta el propósito de la situación, a saber, propiciar la identificación de características que determinan la congruencia de dos figuras. Lo anterior, además, posibilitaría entrar en una discusión álgida sobre la gestión de las puestas en común. Ésta es la base sobre la que se tejería la colaboración entre todos los integrantes del colectivo.
2) Las implementaciones y su análisis. Las implementaciones se analizan y caracterizan como un recurso que enriquece la discusión en el colectivo y promueve las participaciones de sus diferentes integrantes. Para los maestros, estas implementaciones posibilitaron apropiarse de las situaciones, comprender mejor el proceso de aprendizaje de sus estudiantes, para volver a ciertas dimensiones de su enseñanza (Bednarz et al., 2001). Para los investigadores, constituyeron el principal referente para estudiar el proceso de apropiación de las situaciones por los maestros. Y para ambos, proporcionaron conocimientos sobre el funcionamiento de las situaciones y sobre aspectos de éstas que pueden mejorarse.
Las experiencias compartidas tuvieron un doble beneficio: cada maestro aportaba al colectivo su experiencia en la gestión de las situaciones y, al mismo tiempo, recibía una retroalimentación de los demás integrantes sobre dicha experiencia. Desde la investigación, nos interesó analizar cómo los maestros organizaron la clase y qué decisiones tomaron para configurar el medio16 de los estudiantes en cada situación didáctica. A su vez, analizar las producciones de los estudiantes —que los maestros llevaban a las sesiones colectivas— a fin de identificar los conocimientos geométricos que tenían disponibles y la manera en que los funcionalizaron para dar solución a una tarea específica; estas producciones constituyeron la materia básica con la que interactuaron los maestros.
La cooperación
Esta etapa corresponde a la exploración en campo; en este estudio, refiere a la puesta en marcha del dispositivo de formación, donde, a través de las sesiones colectivas y las implementaciones en aula, se establecieron las condiciones para generar acciones reflexivas y oportunidades de formación entre los distintos integrantes. Así, el dispositivo establece el proceso de exploración de formas de enseñanza de ciertas nociones de geometría que conduce a la construcción conjunta, una coproducción entre los socios de investigación.
Un recurso metodológico que apoyó el funcionamiento del dispositivo fue la observación de las implementaciones que realizaron los docentes por parte de los investigadores, la cual estaba sujeta a sus condiciones institucionales, tiempos y el criterio de los maestros (por ejemplo, sólo en algunos casos fue posible videograbar las implementaciones). Este recurso nos permitió tener acceso directo a información sobre la apropiación17 de las situaciones por los docentes y la participación de los estudiantes. Además, otorgó herramientas para retroalimentar y enriquecer el análisis de las experiencias en el marco de las sesiones colectivas. En cambio, optamos por no plantear de entrada la posibilidad de observaciones entre los mismos maestros, por considerar que, además de ser muy difícil la organización y coincidencia de sus horarios, podría ser vivida con cierta tensión18.
La coproducción
Esta última etapa refiere al análisis de los datos a la luz de los objetivos que orientaron la experiencia colaborativa con los docentes. Se consideró que la colaboración representa beneficios para los distintos participantes, preocupaciones e intereses de los mundos que ambos representan: el de la investigación y el de la práctica (Desgagné, 2007). En nuestro caso, se trató de analizar el funcionamiento del dispositivo, en particular, las participaciones de los docentes y de los investigadores, así como las clases impartidas por los docentes, en busca de valorar el grado en que se cumplió el propósito de brindarles una experiencia formativa respecto de la enseñanza de la geometría.
Un producto más que resultó del trabajo con los maestros fueron los conocimientos que se podrían desprender de la experiencia sobre el funcionamiento de las situaciones didácticas, y sobre aquello que convendría comunicar a un docente para que él pudiera aprovecharla de la mejor manera.
Con respecto al producto de los investigadores, éste se constituye en el conjunto de conocimientos que se derivan del análisis de los datos. Conviene señalar que en esta etapa somos los investigadores quienes nos enfrentamos “solos” a dicho análisis de los datos y el saber que deberá producirse (Desgagné, 2007). La idea de colaboración y co-construcción no implica necesariamente que los docentes participen en tareas formales de investigación, pues el sentido que orientó su vinculación al trabajo con los investigadores fue el de cuestionar, analizar y mejorar su práctica docente (Desgagné et al., 2001).
Resultados y discusión
En las experiencias de trabajos colaborativos entre investigadores y maestros existe la tendencia a destacar el conocimiento construido en colaboración y no las formas de colaboración que se dieron y que posibilitaron la construcción de ese conocimiento. En este artículo nos interesamos por esclarecer precisamente las formas concretas que asumió la colaboración a lo largo del estudio, bajo la pregunta: ¿Qué significa colaborar en el marco del trabajo conjunto?
Desde el enfoque de la colaboración para la investigación se busca una influencia entre la práctica y la investigación que permita la co-construcción de un conocimiento mejor adaptado a las necesidades de la práctica. En nuestro estudio, esta idea se materializó en las formas de participación que cada uno de los actores asumió en los distintos momentos del trabajo y que dieron lugar a reelaboraciones en la forma de comprender las situaciones didácticas y a nuevas formas de hacer en el aula a medida que avanzaba la experiencia de trabajo conjunto. A continuación, nos centraremos primero en las formas de colaboración de los maestros y luego en las de los investigadores, apoyándonos en algunos casos con ejemplos.
¿En qué colaboraron los maestros?
Hubo algunas formas de colaboración que fueron promovidas por las condiciones en las que se diseñó y desarrolló el dispositivo, entre las cuales destacamos las siguientes: i) en los momentos de planeación de las sesiones grupales, los maestros compartieron su manera de comprender las situaciones, anticipaciones sobre las posibles producciones de sus estudiantes y los recursos de intervención que creían favorables para llevar las situaciones al aula; ii) posteriormente implementaron las situaciones en sus aulas dejando ver con ello aspectos de su práctica y de sus contextos de práctica —concepciones de enseñanza, de aprendizaje, ejemplos de rutinas y formas de hacer en el aula, organización escolar, etc.—; iii) permitieron un observador externo en sus aulas, quien posteriormente haría comentarios públicos en el colectivo sobre su clase; iv) compartieron con el colectivo su experiencia en el aula y la forma en la que sus estudiantes vivieron la situación; v) recibieron una retroalimentación de ésta por parte de los demás integrantes del colectivo y, a la vez, ofrecieron una retroalimentación cuando sus compañeros compartieron la suya. A continuación, analizaremos algunas de estas colaboraciones.
• De la reflexión individual a la reflexión colectiva sobre la experiencia.
En la última sesión colectiva, tras la implementación de la tercera situación, Ignacio compartió la dificultad que observó en uno de sus grupos de estudiantes para considerar los ángulos, tras haber encontrado el criterio de congruencia de triángulos que consiste en determinar la medida de los tres lados (LLL). El maestro precisó algunos detalles sobre su gestión: el uso de hojas cuadriculadas para presentar las figuras modelo y una consigna en la que inesperadamente prohibía el recurso a medidas. En su reflexión, destacó su desconcierto por no haber llegado a los otros dos criterios de congruencia. Frente a esto, se dio la siguiente interacción en el colectivo:
M. Ignacio: […] En ese grupo los triángulos que les dimos venían en cuadrícula y todos los demás no, todos los demás venían en hoja blanca; es el único grupo en que pasó eso. No sé si tenga algo que ver, la verdad no sé si al ver los cuadros nada más se … porque también me decían [los estudiantes]: le podemos decir cuántos cuadritos; y les digo: no, porque eso es dar unidades, es dar una medida. Y ahí me insistían que si cuadritos, y yo: no, no se puede. Pero de ahí no pasaron... y ya no llegamos a nada.
Investigador: Ok, pues comentarios, ¿cómo ven compañeros? ¿qué pudo haber pasado ahí? [Pregunta a los demás integrantes del colectivo.]
M. Liliana: Pues yo creo que sí influyó mucho que hubiera utilizado la hoja de cuadrícula porque todos quieren sacar las cosas de acuerdo con lo que nos están dando, entonces nos están dando cuadritos, pues agárrate de los cuadritos. Y en ese momento decirles: no, los cuadritos no los puedes tomar; y ellos dirán: ¡pero si me los estas dando!
M. Ignacio: Pero para el segundo criterio, en el primero sí salió LLL [en la primera aplicación], en el segundo [segunda aplicación], nada, nunca obtuve la palabra ángulo por ningún lado.
M. Sara: Yo creo que también un poquito las instrucciones, como bien lo menciona. Me hace ruido esta cuestión que usted les dijo que no podían incluir medidas [comenta a Ignacio].
M. Ignacio: Ninguna medida, sólo de ángulos. O sea, no pueden dar ninguna distancia
M. Sara: ¿Tú esperabas que saliera AAA [criterio ángulo-ángulo-ángulo]?
M. Ignacio: Ajá, y entonces era ver que, si eran los tres ángulos, [entonces] ¿por qué hubo triángulos más grandes que otros? Entonces era ver que a lo mejor era limitarlo con las medidas de los lados.
Investigador: Pero dijiste ninguna medida…
M. Ignacio: Ninguna medida en cuanto a lado. Les dije: lo único que no pueden hacer es dar la medida de ningún lado. Inclusive les ayudamos al final y les dijimos: Pueden dar la medida de un lado, nada más de uno... y ni así.
M. Sara: Yo creo que sí fue por eso, yo creo que ellos se cerraron mucho al decir: ¿Ninguna medida?, como que sí les hizo mucho ruido esa cuestión y por eso se bloquearon, no supieron como por dónde. Si al final lo que ellos esperaban era que los triángulos tuvieran la misma medida de sus lados, al ya no indicar ninguna medida, pues ellos decían: ¿pues entonces cómo? (Castaño, 2021, p. 204).
Sara y Liliana movilizaron su conocimiento sobre la congruencia de triángulos (es necesario proporcionar medidas; proporcionar sólo las medidas de los ángulos da lugar a figuras semejantes, pero no necesariamente congruentes) y también conocimientos pragmáticos, adquiridos en su experiencia (lo que se dé a los estudiantes para resolver un problema, aún sin intención didáctica, puede ser interpretado por ellos como que debe usarse).
Las aportaciones de las dos maestras fueron pertinentes y parecían responder a la expectativa de Ignacio de comprender el porqué de la dificultad de sus estudiantes. Lograron analizar y comunicar dos aspectos didácticos importantes: la manera en que la consigna se dio, y el medio material que se organizó (en particular la hoja cuadriculada) condicionaron las interacciones de los estudiantes con la situación. Por otra parte, Sara ayudó a que Ignacio explicitara el objetivo que perseguía con esta consigna: que apareciera el criterio AAA, a fin de mostrarle a los estudiantes una combinación de datos que garantizaría la forma, pero no la congruencia.
Esta interacción que se sostuvo en el colectivo configuró un episodio de colaboración que permitió a los maestros reflexionar sobre su enseñanza; Ignacio desde su propia práctica y Liliana y Sara desde la posibilidad de interpretar una experiencia en el marco del mismo proyecto de enseñanza. En particular, la colaboración estuvo en las diferentes acciones que se articularon para lograr una reflexión colectiva de la práctica, Ignacio al compartir las decisiones que tomó para la implementación, las dificultades que tuvo y su interés por comprender lo ocurrido en el aula y, Sara y Liliana, al ofrecer con sus participaciones la posibilidad de enriquecer el ejercicio reflexivo que estaba haciendo Ignacio sobre su propia clase.
• Un banco de recursos posibles de intervención para gestionar la puesta en común.
La experiencia con la situación 1 (la figura por comunicar es un rectángulo con alguna diagonal o línea paralela a uno de sus lados) dejó ver a la puesta en común como la fase más difícil de gestionar para todos los maestros, por lo que, para la planeación de la segunda situación, ellos se interesaron por prever estrategias que les ayudaran en su gestión. En la tabla 1 presentamos los recursos que surgieron:
Table 1. Recursos para la gestión de la puesta en común previstos por los maestros para la situación 2 (la figura por comunicar es un paralelogramo).
| Recurso 1: Hacer evidentes los errores en los mensajes | |
| M. Liliana | Propuesta: La maestra como emisora – los estudiantes como receptores19 M. Liliana: Yo lo hice con uno de mis grupos más indisciplinados y dije: Bueno, esto es un fracaso [ríe]. Yo les fui dictando las indicaciones precisas: a ver, número uno. trazamos una línea, y ya le estoy diciendo cómo y ellos dicen: ¡pero maestra!, y ya les digo: pues una línea horizontal o vertical… y luego les digo que trazamos un ángulo y ellos dicen: pero ¿cómo un ángulo?, ¿hacia dentro o hacia afuera? |
| M. Sara Propuesta 1 | Propuesta: Construir la figura con “mi propio mensaje” M. Sara: [decirles a los estudiantes] Con las reglas que tu construiste, intenta hacer las figuras que tú quieres, y a lo mejor se dan cuenta de que no va a salir porque mis reglas no son suficientes...podría ser también otra opción… con las mismas que ellos escriben, construyen con esas reglas. |
| Recurso 2: Elaborar un mensaje nuevo y desechar los erróneos | |
| M. Sara Propuesta 2 | Propuesta: Construir con los estudiantes un mensaje para toda la clase y construir la figura M. Sara: […] la otra opción sería que, en la socialización, cuando nos demos cuenta de la necesidad de algunos [datos], entre todos construyamos un mensaje que sea claro, que podamos seguir las indicaciones y logremos que se construya la figura. Investigador: Es buena idea. Yo lo dejaría ya para cuando no va a haber chance de más, de aplicarlo otra vez […] porque ya con eso casi cierras. |
| Recurso 3: Validar de entrada un procedimiento que se espera que hagan los estudiantes | |
| M. Michelle - M. Ignacio |
Propuesta: Seleccionar y discutir “buenos” mensajes M. Michelle: […] uno va escogiendo cuáles son las mejores indicaciones [en los mensajes]; a la siguiente sesión, ya lo que se hace es que con los que hayamos escogido, planteárselos a los estudiantes, poner la imagen [la figura modelo] y empezar… M. Ignacio: O mejor el peor [mensaje] y entre todos reconstruir una indicación correcta Investigador: Exacto, uno con errores que pueden ser muy interesantes para compartir y otro con logros también muy interesantes |
| Recurso 4: Confiar en los “aprendizajes” de los estudiantes | |
| M. Fabio | Propuesta: Apoyarse en los acuerdos establecidos en la situación 1 M. Fabio: […] pues [apoyarse] con los acuerdos que hiciste […] Cada vez que tu dabas un acuerdo es porque era una definición establecida y comprobada; si pasas a los acuerdos que tu diste, ahí efectivamente puedes ir con tus acuerdos y construyes la figura... ¡es más fácil! |
Nota: Tomado de Castaño (2021, pp. 88-89).
Las estrategias que se propusieron, si bien estaban en el marco de la puesta en común, tenían propósitos distintos en relación con el trabajo de los estudiantes. En algunos casos, los demás maestros o el investigador aportaron sugerencias para ayudar a repensarlas y mejorarlas. Por ejemplo, la propuesta de Michelle —practicante de Ignacio que asistió a dos sesiones colectivas— sugería discutir con los estudiantes ejemplos de “buenas producciones”. Frente a esto hubo dos reacciones en el colectivo, la de Ignacio, que estaba más en sintonía con las propuestas de Liliana y Sara —detectar errores para luego construir buenas descripciones— y la del investigador, que sugería un equilibrio entre lo que proponían los dos maestros.
La dificultad experimentada por los maestros con la situación 1 sirvió para que centraran su atención en la gestión y desató algunas formas de colaboración que ya se estaban consolidando en el colectivo: compartir formas de hacer en el aula que se consideran útiles para alcanzar los objetivos con los estudiantes y aportar ideas para complementar o ajustar las propuestas que surjan.
• Las producciones de los estudiantes, sus dificultades.
En la última sesión colectiva, los maestros destacaron las dificultades que tuvieron los estudiantes para llegar a los criterios de congruencia de triángulos —situación 3—, sobre todo, los que involucraban los ángulos.
La siguiente intervención de Sara destacó en particular la dificultad del criterio “ángulo-lado-ángulo” [ALA]:
M. Sara: […] yo sí esperaba que el último criterio [ALA] fuera un poquito más complicado para ellos, porque ellos precisamente referían... [unos segundos en silencio] ¿Puedo dibujar? [pregunta al investigador]
Investigador: Sí, claro
M. Sara: [pasa al pizarrón] […] si el lado mide 8 cm y el ángulo 45º y el otro, por ejemplo 95º, obtienen el triángulo hasta que se prolonguen [los segmentos, los lados del triángulo], entonces ése es el más complejo para ellos en ese sentido, porque ellos tienen que visualizar que deben de prolongar [ilustra su ejemplo con un dibujo. Véase la figura 1] y ése es el que me estaba costando con los estudiantes que lograran.
Figura 1. Ejemplo de criterio ALA por Sara
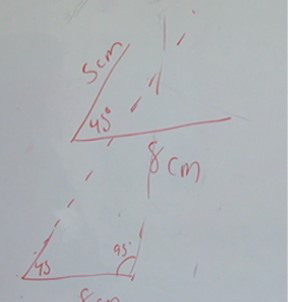
Fuente: Castaño (2021, p. 200).
Por su parte, Liliana mencionó lo siguiente:
M. Liliana: […] les pregunté [a los estudiantes]: ¿De qué otra manera se puede trazar otro triángulo de igual medida y de forma pero que ya no sea con lo que yo te di [los datos]?; entonces los chicos empezaron a decir: Ah, puede ser base y ángulo y ángulo. Les digo: A ver, trázalo. Y ya lo trazaron y una niña se quedó trazando los ángulos, y me decía: Maestra, ¿y luego cuánto de lado? [porque le había dado ALA] y ya le dije: pues prolóngalos a ver qué pasa; así como decía Sara, cuando van prologando y llegan a la punta y comprueban entonces ellos también se admiran y dicen: ¡es que con esto fue suficiente para poder lograrlo! (Castaño, 2021, p. 200).
Así, con respecto al criterio “ALA”, las maestras pusieron en evidencia que para los estudiantes era difícil aceptar que con los dos lados “que faltaban” era posible construir el triángulo, pues no les era fácil ver: i) que el tercer vértice quedaba determinado al prolongar las rectas que contenían dos de sus lados y ii) que el triángulo obtenido sería idéntico al original porque las longitudes de los dos lados que se prolongaban también quedaban determinadas. Estos hechos resultaron sorprendentes para algunos de sus estudiantes. De acuerdo con Perrin y Godin (2018), esta dificultad se explica por la necesidad, en estas tareas de reproducción, de que los estudiantes vean unidades figurales (línea, puntos) no explicitadas en la figura, a partir de aquellas presentadas.
Las precisiones de las maestras sobre la dificultad del criterio pusieron en evidencia que la intención didáctica que se enfatizó para esta tercera situación con los maestros priorizó los criterios de congruencia, pero dejó de lado aspectos como la previsión de estrategias de intervención para lograr este objetivo. Recordemos también el primer ejemplo de este apartado en el que destacamos la dificultad de Ignacio para ayudar a sus estudiantes a avanzar hacia los criterios que involucran ángulos. Frente a esto, encontramos que los mismos maestros avanzaron en la dirección de prever estrategias para la puesta en común, algunas más efectivas que otras; por ejemplo, Liliana optó por involucrar a todos los estudiantes en la construcción de un mismo triángulo con los mismos datos, para luego solicitar otras combinaciones de datos para construirlo.
A partir de las aportaciones de los maestros, los investigadores inferimos tres asuntos. El primero, la necesidad de que, como investigadores, comunicáramos con más claridad los distintos objetivos que se preveían con la situación, pues en la sesión de planeación el objetivo de reproducir el triángulo de manera idéntica y el de obtener los criterios quedaron sobrepuestos; el segundo, la necesidad de hacer ajustes a la situación didáctica en relación con la formulación de los criterios de congruencia, agregando actividades previas que favorezcan que los estudiantes aprendan a construir triángulos con regla y compás a partir de ciertos datos; y el tercero, la necesidad de movilizar diferentes recursos para hacer frente a las dificultades y poder avanzar hacia los criterios. Estos tres asuntos constituyeron conocimientos que surgieron de la construcción conjunta (reflexiones de los maestros que suscitaron reflexiones posteriores de los investigadores) y que ayudarían a mejorar la factibilidad de la situación didáctica y el buen funcionamiento del dispositivo. La idea de colaboración que destaca una influencia entre la práctica y la investigación y que permite la co-construcción de un conocimiento mejor adaptado a las necesidades de la práctica, se aclara al materializarse en un episodio como éste.
• El maestro como observador de la clase de su colega.
Al final de la primera sesión, un maestro, Fabio, propuso observar la clase de su colega Sara. Éste fue el único caso de observación entre pares que se realizó20. Dejó ver una forma de colaboración con un alto valor formativo por la posibilidad de ofrecerle a un colega una retroalimentación de los aspectos observados. A continuación citamos la aportación que hizo Fabio a Sara sobre su clase:
M. Fabio: […] la profesora empezó [la puesta en común] con el niño que tenía contra la pared, que era muy insistente y a cada rato quería participar … y luego la niña del medio también, y ya de repente por ahí otro que empezó a salir… pero nada más se basa en esos cuantos, entonces, también hubiera sido bueno que hablaran los que andan por ahí [en silencio] […] Entonces para la cuestión de la participación, a veces yo siento que no nada más es dejarlos que estén los mismos, hay que agarrar a otros para que así pues ver qué piensan y nos pueden dar algo, a lo mejor el que está bien tímido nos puede dar la solución frente al que es el más apto.
La sugerencia de rescatar las contribuciones de estudiantes con baja participación para posicionarlas en las discusiones grupales es desafiante tanto para los maestros como para los estudiantes. Resultó interesante que esta característica fuera señalada por el docente que tuvo más dificultades con la implementación, a la docente que tuvo el desempeño más destacado, lo que deja ver que las dificultades que este docente experimentó, en aspectos muy específicos de la gestión de la situación, no le impidieron detectar debilidades en otros aspectos, más generales, en la gestión de su colega, lo cual seguramente enriqueció los intercambios. Conviene precisar que este episodio de observación entre pares se dio con maestros que pertenecían a la misma escuela y tenían una relación laboral y personal de varios años; consideramos que esta condición fue fundamental para que accedieran a las observaciones. Este es un ejemplo en el que aparece la retroalimentación como una forma de colaboración.
• Retomar ideas que nacieron en el colectivo para la propia gestión.
En los espacios de planeación se analizaron algunas variantes de las situaciones. Ése fue el caso de las características de las figuras que servirían como modelos para el juego de comunicación. Para la situación 2, se consideró la posibilidad de hacer al menos dos aplicaciones y, con ello, dar a los estudiantes una segunda ocasión de abordar la situación con los aprendizajes que hubieran logrado en la primera. Frente a esto, la propuesta del investigador fue incluir más modelos, entre ellos rombos y romboides y con diferente posición respecto de los bordes de la hoja. Fabio, un maestro que con la situación anterior había tenido el problema de las miradas indiscretas de los estudiantes receptores a las figuras que describieron los emisores antes de la superposición, encontró en la propuesta una solución a esta dificultad. En las implementaciones de los maestros quedaron en evidencia las distintas interpretaciones que cada uno dio a este aspecto. Liliana, por ejemplo, incorporó rombos y romboides, cada figura con trazos de una diagonal o un segmento paralelo a uno de los lados del paralelogramo —véase la figura 2—. Esta decisión introdujo una variable didáctica que no estaba prevista para la situación, que la hacía más compleja y desplazaba desafíos como la dificultad del ángulo interior o la altura. Incluso, se corría el riesgo de desplazar el objetivo de analizar paralelogramos desde el punto de vista de sus propiedades —en una dimensión—, y que lo vieran más como un ensamblaje por yuxtaposición de otras figuras.
Figura 2. Figuras modelo para la situación 2 propuestas por Liliana
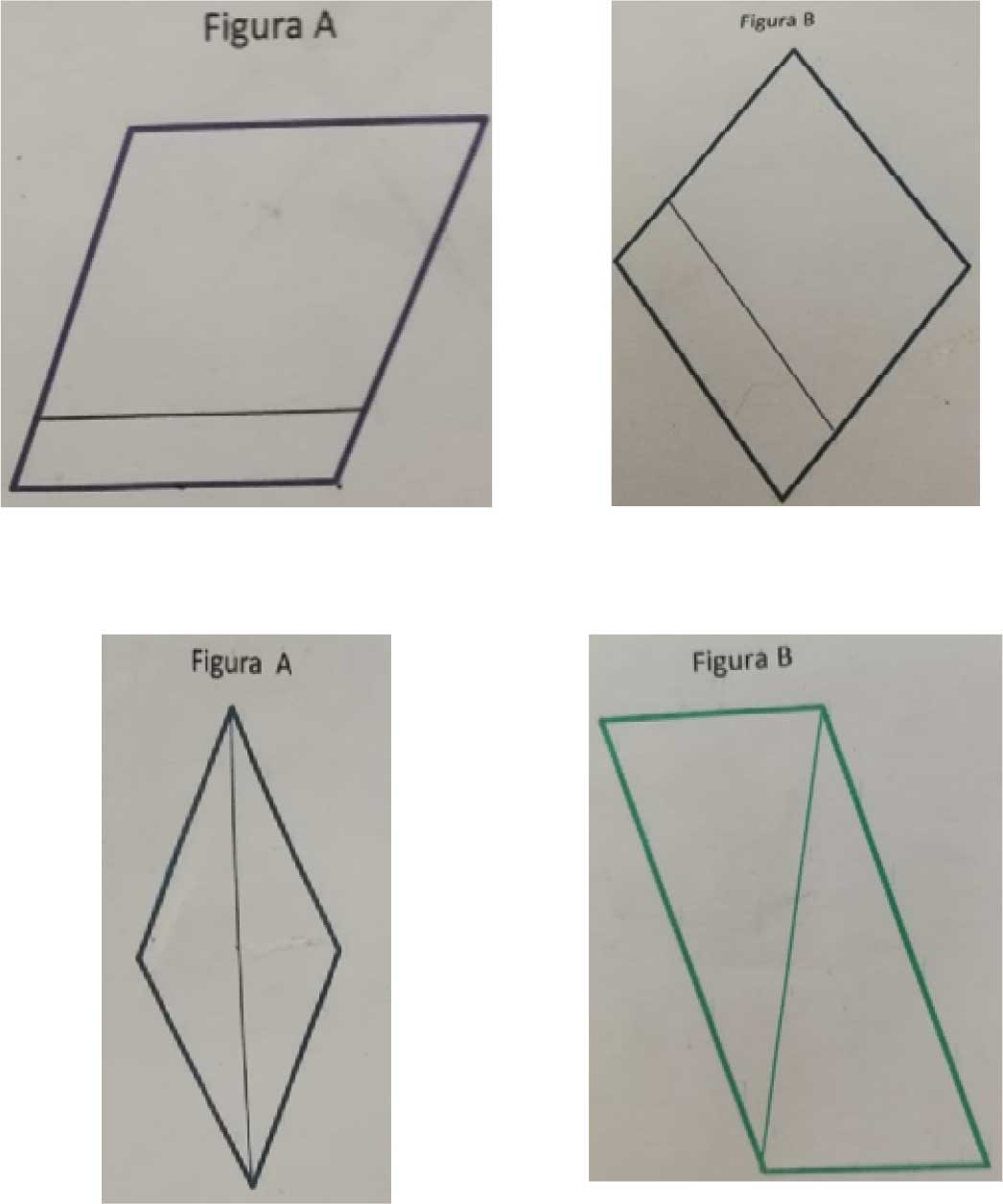
Fuente: Castaño (2021, p. 98).
Por su parte, Fabio incorporó modelos de figuras en madera que, aunque redujeron el efecto de la posición de la figura respecto de la hoja y facilitaron la validación de las figuras evitando que los giros e inversiones les dificultara determinar la congruencia, provocaron que atributos como el material o el grosor se consideran a la par con las características geométricas, confundiéndose con ellas —véase la figura 3—.
Figura 3. Figuras modelo para la situación 2 propuestas por Fabio

Fuente: Castaño (2021, p. 95).
Con este episodio podemos referir a dos asuntos: por un lado, que la relación que se da entre maestros e investigadores está inmersa en un juego de encuentros y desencuentros respecto de las interpretaciones que unos y otros tuvimos frente a una misma propuesta o tema de discusión, pero que, visto en la perspectiva de un proceso de mediano plazo estos desencuentros también pudieron ser fuentes de aprendizaje para todos. Por otro lado, que era esperable una diversidad de formas de materializar la propuesta en el aula considerando los procesos de apropiación de las situaciones didácticas que experimentan los maestros en el marco del dispositivo. Sin embargo, lo que nos interesa destacar es que en algunos momentos se evidenció cómo los maestros adoptaron ideas, recursos o propuestas que fueron construidas en las discusiones colectivas con la intención de enriquecer y mejorar sus propias implementaciones. Esto último abona a su formación continua y, por tanto, puede considerarse una forma de colaboración que ayuda a lograr el objetivo del dispositivo.
En síntesis, algunas de las formas de colaboración se mantuvieron a lo largo de toda la experiencia colaborativa, mientras que otras, que nacieron en el marco del trabajo conjunto, se dieron sólo en ciertos momentos —como la observación entre pares—. Asimismo, hubo formas de colaboración que se vincularon directamente con el enfoque de trabajo colectivo que caracterizó al dispositivo, por ejemplo, que los maestros participaran en dinámicas que resultan ajenas para su práctica, pero favorables para un proceso de formación continua —como permitir observadores externos, hacer pública su práctica y exponerla a análisis colectivos, y otras tuvieron relación directa con el contenido geométrico de las situaciones didácticas —como la idea de Liliana de agregar segmentos adicionales en las figuras modelo o la de Fabio de diseñarlas en madera—.
¿En qué colaboran los investigadores? Posibilidades y tensiones
La colaboración de los investigadores se centró en proporcionar condiciones favorables, logísticas y de contenido matemático-didáctico, para que se diera un trabajo colaborativo con los maestros: i) proponer las situaciones didácticas y aclarar su objetivo, enfoque didáctico, fases y algunas orientaciones para la gestión; ii) regular el trabajo colectivo, procurando dar voz a los docentes, valorar sus aportaciones, evitar posturas autoritarias que rompieran la simetría buscada en la colaboración y, a la vez, encausar las discusiones a fin de evitar que se alejaran del tema o se estancaran y, iii) retroalimentar las experiencias en aula de los maestros con base en la observación directa y las reflexiones individuales y colectivas que surgían sobre estas. Nos interesa profundizar en este último segmento.
Identificamos distintos tipos de retroalimentación por parte de los investigadores: desde episodios en los que no logramos dar una retroalimentación, otros en los que nos faltó ser más claros y contundentes respecto de la idea que queríamos comunicar y, finalmente, otros pocos, en los que logramos comunicar alguna observación con claridad y precisión (Castaño y Block, 2021).
• Retroalimentaciones directas y otras poco contundentes. La posición de la figura en la noción de congruencia.
En la sesión colectiva posterior a la implementación de la situación 2 se analizó un mensaje producido por un equipo de estudiantes de Liliana. La estrategia que se adoptó fue que Ignacio se asumiera como receptor y trazara la figura en el pizarrón. El mensaje resultó correcto para reproducir la figura, pero Liliana aclaró que no fue el caso de los estudiantes receptores porque “les había quedado del otro lado”. Frente a esto, se dio una amplia discusión en el colectivo que dejaría a la luz diferencias conceptuales de los distintos actores sobre la congruencia21. En la tabla 2 presentamos el mensaje, la figura original y la reproducida por los estudiantes. Conviene aclarar que los lados y ángulos de las dos figuras —la original y la reproducida— eran iguales:
Table 2. Ejemplo de mensaje, figura modelo y reproducida. Estudiantes de Liliana
| Mensaje | Figura modelo | Figura reproducida |
| Hacer una línea horizontal de 2.8 cm y luego hacer una línea imaginaria de 5.9 cm en el centímetro 1.4 hacia arriba. Se hace la línea de 2.8 hacia la izquierda, se hace una línea inclinada uniendo los dos extremos derechos y enseguida se hace otra línea inclinada uniendo los dos extremos izquierdos. |
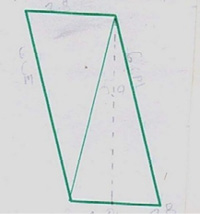
|

|
Fuente: Castaño (2021, p. 133).
La discusión fue la siguiente:
M. Liliana: […] lo interpretaron mal porque les dio del otro lado [a los receptores]… estos chicos lo interpretaron del lado derecho y aquí con el maestro [Ignacio] dio bien con el original.
Investigadora: Eso está aquí [lee el mensaje]: “se hace la línea de 2.8 cm hacia la izquierda” y ellos [los receptores] lo hacen hacia la derecha.
M. Liliana: Pero no es…
Investigador: A ver maestros, pero si la posición cambia, ¿la figura ya no es igual?, es decir, ¿si está inclinada para el otro lado ya no es un paralelogramo igual?
M. Fabio: No
M. Liliana: No… pues ésta [la figura modelo del mensaje que se estaba discutiendo] yo la tuve que poner así y así y ya dio [gira y luego invierte la figura]
M. Ignacio: Sí, como espejo
Investigador: Entonces, necesitaríamos acordar si para poderse llamar igual no se vale rotar o sí se vale rotar.
M. Sara: Sí, porque entonces ya en las instrucciones se estaría formando una figura distinta a la que nosotros les dimos, por la orientación tal vez de un lado o de un ángulo.
Investigador: Si acordamos que no se vale rotarla entonces no son congruentes [el caso que se está estudiando de Liliana].
M. Liliana: Por eso no les puse palomita, porque a mí me llamó mucho la atención porque yo dije: parece que son congruentes; y por más que lo ponía y lo ponía a girar hasta que le tuve que hacer así [invertir la figura modelo] y así, sí ya son congruentes (Castaño, 2021, p. 133).
Para los maestros, la posición en la que resultaba la figura importaba para establecer la congruencia. No estaba en discusión que los lados y ángulos de las figuras fueran iguales, sino la validez de realizar acciones adicionales como girar o voltear la figura reproducida para hacerla coincidir con la original. Ante la unanimidad de los maestros, y un claro pero implícito desacuerdo del investigador, la discusión continuó:
Investigador: Entonces, decidimos si se vale o no se vale girarla para el criterio de congruencia… ¡yo creo que sí se vale!
M. Ignacio: Porque, por ejemplo, en el uso que a lo mejor alguno de ellos le podía dar… que llegara a ser hijo de herrero o carpintero, ¡no funciona!
M. Liliana: No, ya no queda
M. Fabio: ¡O cuando tú cambias la chapa de una puerta!
M. Ignacio: Exactamente.
M. Fabio: Es la misma, pero te dicen: derecha o izquierda.
M. Liliana: Sí, y ya no es funcional.
Investigador: [Ríe] como dirían en francés, “touché” o sea, ¡me dieron! [ríe].
Colectivo: [Ríe. Pasan algunos segundos].
Investigador: Pero, llevando un poco la discusión más lejos, [es necesario] distinguir el criterio de congruencia ya en geometría, de la congruencia ya aplicada en cosas prácticas como la del herrero y eso… pero, bueno, de todas maneras, queda como la discusión…
M. Ignacio: Sí.
M. Sara: A mí me pasó lo mismo. En el caso del primer romboide, les pasó a muchos [estudiantes], ¡a muchos!; entonces ellos sí dijeron: no son iguales. Y, obviamente se dieron cuenta de que si yo volteaba probablemente coincidían, pero sí les pasó a muchos, que era la misma [figura], pero la tenían que girar
Investigador: Entonces, si nosotros decimos dos paralelogramos que tienen sus dos lados iguales y su ángulo entre los lados igual, ¿pensamos que con eso era suficiente, con dos lados y el ángulo…?
Colectivo: Sí.
Investigador: Pero si nos atenemos a que esos dos no son congruentes [el ejemplo de Liliana], quiere decir que esos criterios no son suficientes, entonces les falta algo más, ¿verdad?
M. Fabio: Para su nivel, yo creo que consideraría que sí son congruentes […]
Colectivo: Sí (Castaño, 2021, pp. 134-135).
Como se observa, el investigador no logró persuadirlos de descartar esta idea de congruencia que se asomaba. A pesar de que se concluyó que las figuras del ejemplo sí eran congruentes, la validez del argumento de la funcionalidad de la posición en contextos extramatemáticos, sumado a las intervenciones poco contundentes del investigador, dejó en el ambiente una idea errónea: que la posición también podía determinar la congruencia.
Después de este episodio, en la sesión de análisis de la implementación de la última situación el investigador retomó este asunto de la congruencia en las observaciones que hizo a Sara sobre su clase:
Investigador: […] volvió a aparecer el hecho de que hay un triángulo que quedó bien [idéntico al original], pero ubicado para el otro lado; y entonces: ¿quedó igual? Sí, sí y todo sí, pero un alumno dijo, pero volteado para el otro lado. Y entonces tú aceptaste que eso hacía que no fueran congruentes y dijiste: Pues… ¿qué había hecho falta para que hubiera quedado del mismo lado? Entonces, bueno, nada más recuerden que quedó pendiente, aquí para nosotros, averiguar si el hecho de que queden volteados para el otro lado [los triángulos] hace que no sean congruentes; o si uno puede definir la congruencia como uno quiera. Bueno pues, para mí, congruencia va a ser que yo sin voltearlos los puedo superponer o si congruencia es si los puedo superponer volteándolos y eso […] ¿Se acuerdan de la traslación y la rotación?, ésas son trasformaciones que no modifican a la figura, nada más la mueven. Entonces la simetría axial lo que hace es volteártela y, por lo tanto…
M. Sara: Sí son congruentes [interrumpe al investigador].
Investigador: Sí son congruentes… o si las recortas y ya las tienes sueltitas, también se pueden encimar (Castaño, 2021, p. 197).
Esta vez el investigador fue más claro en su intervención y, en general en la retroalimentación que dio a la maestra. Su intención fue aclarar la noción de congruencia que había quedado “suelta” y que seguía apareciendo en las clases de los maestros.
Desde el diseño del dispositivo se consideraron dos fuentes de retroalimentación para los maestros: la clase y las sesiones colectivas; considerando que eran fuentes de gran riqueza formativa para ellos. El caso anterior fue uno de varios en los que dar una retroalimentación resultó difícil, y se terminó limitándola. Algunas razones que explican esta dificultad están vinculadas a nuestra interpretación de los principios del enfoque colaborativo; otra fue el temor de perturbar el clima de trabajo que se estaba logrando construir con los maestros, y, finalmente, otras más tienen que ver con las condiciones de trabajo en las que se puso en marcha el dispositivo. Veamos.
La búsqueda de la simetría de posiciones en relación con la co-construcción del conocimiento. Esto tiene que ver con la intención de no ser demasiado directivos en las sesiones de planeación en relación con la forma en que los maestros implementarían las situaciones en el aula, es decir, de no ser autoritarios y dar indicaciones carentes de clara justificación o que apelen al “saber matemático” sin más explicación. Asimismo, de evitar comentarios críticos sobre las clases observadas que pudieran interpretarse como una evaluación de sus prácticas y que en consecuencia afectara la participación de los maestros en el colectivo.
Definiciones matemáticas incompletas o erróneas. Comunicar a los maestros que algunas de las dificultades que tuvieron en las aulas se debían a nociones matemáticas incompletas o erróneas fue difícil para los investigadores, pues de cierta manera implicaba para nosotros interpelar su legitimidad en términos de su saber matemático. Al unirse a un trabajo con otros colegas e investigadores, los maestros manifestaron su interés por conocer situaciones didácticas y formas de hacer en el aula que les ayudaran a mejorar sus prácticas en relación con la enseñanza de la geometría, es decir, un interés centrado en la didáctica de la geometría, mas no en la geometría misma. En efecto, esto pudo evidenciarse a lo largo de la experiencia colaborativa, ya que los maestros tendieron a justificar las dificultades en los estudiantes y no en su propia gestión —recordemos las conceptualizaciones sobre la congruencia de las figuras—. De aquí que pareciera más factible decirle a un maestro que había cosas de su gestión que podían mejorarse —sin que sintiera vulnerado su profesionalismo— que decirle que había aspectos de su saber matemático que debían precisarse. Nos preguntamos si es posible que los maestros consideren que el saber didáctico es, después de todo, relativo, pues hay distintas teorías y éstas evolucionan, mientras que el conocimiento matemático está clara y unívocamente definido y, sobre todo, es lo mínimo que se espera que un maestro de matemáticas domine.
Un clima de trabajo en el que aún no se había construido la confianza suficiente para comunicar a los maestros aspectos por mejorar de su práctica. La relación que se logra construir entre los investigadores y maestros en el marco de un trabajo colaborativo es un factor importante en la riqueza de los resultados que se pueden obtener. De acuerdo con Roditi (2015, en Morellato, 2017), el grado de colaboración depende del compromiso de los distintos actores y de las relaciones de confianza que se logren establecer. En el caso de los maestros, esta confianza hacia los investigadores es fundamental, ya que están haciendo pública su práctica y pueden sentirse vulnerables frente a este hecho. Los investigadores sabemos que esta confianza no está dada de entrada y que debe construirse en la interacción con los maestros. Justamente, lograr estos lazos de confianza ayuda tanto a la comunicación como a la recepción de aquellos aspectos de la práctica de los maestros susceptibles de ser mejorados.
La forma en la que se organizó el trabajo en el dispositivo. Pensamos que el no haber podido organizar reuniones de los investigadores previas a las sesiones colectivas, para discutir y analizar aspectos de las implementaciones observadas, identificar los temas que queríamos destacar con los maestros y prever nuestras intervenciones en el colectivo, influyó en el tipo de retroalimentaciones que ofrecimos. La razón principal fue el escaso tiempo del que se disponía para el trabajo: el ritmo de un encuentro semanal y las observaciones de clases entre uno y otro. Ésta fue una condición institucional de las escuelas a la que nos tuvimos que ajustar para desarrollar la investigación.
La reticencia para cuestionar que caracterizó la mayoría de nuestras participaciones pone de manifiesto dificultades sutiles, pero no sin consecuencias, en el proyecto de promover y sostener un principio de simetría de trabajo con los maestros, sobre todo en la retroalimentación de sus prácticas. Consideramos que, para desarrollar y sostener este tipo de investigaciones, los investigadores movilizan un conocimiento asociado a su marco didáctico y acorde al enfoque colaborativo, que les permite justamente promover y sostener una simetría de trabajo. Este conocimiento tiene la característica de ser implícito y aparece de manera espontánea en la interacción con los maestros. Creemos que este saber hacer es inherente a la colaboración y se gana sólo con más experiencias como ésta (Castaño y Block, 2021).
En este apartado nos interesó mostrar a la retroalimentación como una forma de colaboración por parte de los investigadores. Sin embargo, es destacable que ésta no se dio en el vacío, sino que se articuló con acciones colaborativas que sirvieron como parteaguas para estos episodios de retroalimentación: i) haciendo explícito ante el colectivo los puntos de vista particulares, ii) justificando y dejando ver por qué un enunciado era válido desde nuestra posición como maestro o investigador —como pasó en la discusión sobre la noción de congruencia donde todos expusimos argumentos para defender nuestra posición—, y iii) aceptando el punto de vista sobre determinado asunto, aun sin que fuera muy claro hasta qué punto estaban de acuerdo, o bien, esperando otra ocasión para retomar la discusión. Consideramos que acciones de este tipo son colaborativas porque permiten sostener la interacción en colectivo y avanzar en la construcción de conocimiento. En la literatura, este tipo de acciones se vinculan con la noción de contrato de colaboración (Bednarz et al., 2001).
Conclusiones
Nos interesó mostrar lo que hace colaborativo un trabajo conjunto entre maestros e investigadores respecto del objetivo de ofrecer una experiencia de formación continua a los maestros en torno a la enseñanza de la geometría en secundaria, así como algunas de las dificultades para lograrlo. Nos fijamos principalmente en las maneras en las que participaron los distintos actores y en las condiciones en que se dieron dichas participaciones, para argumentar que éstas configuraron formas de colaboración que abonaron al valor formativo de la experiencia.
Argumentamos que la colaboración aparece y se sostiene por varios factores:
- Por un interés común que fundamenta y moviliza el trabajo de los participantes durante toda la investigación: la mejora de las prácticas de los maestros respecto de la enseñanza de la geometría.
- Por la necesidad del conocimiento del otro para lograr este objetivo común antes mencionado: los investigadores buscando conocer el potencial de las distintas estrategias implicadas en el dispositivo para la formación de los docentes —esto es, el análisis, la adaptación y la implementación en clase de situaciones didácticas, así como la retroalimentación colectiva a dichas implementaciones—, y los maestros, quienes, para fortalecer su conocimiento de didáctica de la geometría, confían en el conocimiento experto de los investigadores sobre ese tema, y sobre el dispositivo puesto en marcha.
- Por la motivación de aportar entre todos al conocimiento sobre la gestión de determinadas situaciones, destacando las principales dificultades de dicha gestión, las formas en que algunas se fueron superando, las adaptaciones que resultaron necesarias para su viabilidad, y aquellas que no resultaron adecuadas.
Destacamos también algunas condiciones que favorecieron un trabajo conjunto, así como la existencia de tensiones que aparecieron y que en ocasiones limitaron la colaboración, sobre todo, la que refería a la posibilidad de los investigadores de ofrecer una retroalimentación a los maestros.
El análisis presentado deja ver algunos aspectos por mejorar y desafíos que se advierten para futuras investigaciones, a saber, un análisis previo de las situaciones más fino respecto de los objetivos con los estudiantes —en este caso, el objetivo de los criterios de congruencia con la situación 3 requería de ciertas variantes de la situación—; retroalimentación a los maestros que se puede enriquecer preparándola con antelación cada vez y con una mayor duración de este tipo de experiencias; la posibilidad de replicar la experiencia, con las situaciones ya mejoradas, involucrando a nuevos maestros.
Bibliografía
Anadón, M., y Couture, C. (2007). La recherche participative. Multiples regards (Introducción). En Anadón, M. (coord.) La recherche participative. Multiples regards (1-11), (205-220). Presses de l’Université du Québec.
Artigue, M. (1995). Ingeniería didáctica. En Ingeniería didáctica en Educación Matemática. Un esquema para la investigación y la innovación en la enseñanza y el aprendizaje de las matemáticas. Goméz, P (ed.), Moreno, L. Douady, R. y Artigue, M. (pp. 33-60). Grupo Editorial Iberoamérica, S. A. de C. V.
Bednarz, N., Poirier, L., Desgagné, S., y Couture, C. (2001). Conception de séquences d’enseignement en mathématiques : une nécessaire prise en compte des praticiens. In Le génie didactique (pp. 43-69).
Block, D., Moscoso, A., Ramírez, M., y Solares, D. (2007). La apropiación de innovaciones para la enseñanza de las matemáticas por maestros de educación primaria. Revista Mexicana de Investigación Educativa, 12(33), 731-726.
Brousseau, G. (1998). Théorie des situations didactiques. Didactique des mathématiques 1970-1990. Collection : Recherches en didactique des Mathématiques. Grenoble : La Pensée Sauvage Èditions.
Castaño, Y. (2021). Trabajo colaborativo entre profesores de secundaria e investigadores. Una experiencia en torno a la caracterización y congruencia de figuras geométricas [tesis de maestría]. Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional.
Castaño, Y., y Block, D. (2021). Interacciones entre maestros, y con investigadores, como recursos de formación. Algunos resultados de una experiencia colaborativa en torno a la enseñanza de la geometría [memoria electrónica]. Congreso Nacional de Investigación Educativa CNIE-2021.
Desgagné, S. (1997). Le concept de recherche collaborative: l’idée d’un rapprochement entre chercheurs universitaires et praticiens enseignants. Revue des Sciences de l’éducation, 23(2), 371-393.
Desgagné, S. (2007). Le défi de coproduction de “savoir” en recherche collaborative. Autour d’une démarche de reconstruction et d’analyse de récits de pratique enseignante. En La recherche participative. Multiples regards (pp. 89-116). Presses de l’Université du Québec. Traducción realizada para el Seminario de Didáctica de las Matemáticas del DIE.
Desgagné, S., Bednarz, N., Lebuis, P., Poirier, L., y Couture, C. (2001). L’approche collaborative de recherche en éducation: un rapport nouveau à établir entre recherche et formation. Revue des Sciences de l’éducation, 27(1), 33-64.
Duval, R. (2016). Las condiciones cognitivas del aprendizaje de la geometría. Desarrollo de la visualización, diferenciaciones de los razonamientos, coordinación de sus funcionamientos. En Comprensión y aprendizaje en matemáticas: perspectivas semióticas seleccionadas. Duval, R y Saénz-Ludlow, A. (pp. 13-60). Universidad Distrital Francisco José de Caldas.
Fregona, D. (1995). Les figures planes comme “milieu” dans l’enseignement de la géométrie: interactions, contrats et transpositions didactiques. L’ Universite Bordeaux I.
Itzcovich, H. (2005). Iniciación al estudio didáctico de la geometría. De las construcciones a las demostraciones. Libros del Zorzal.
Itzcovich, H., y Broitman, C. (2001). Orientaciones didácticas para la enseñanza de la geometría en EGB. Dirección General de Cultura y Educación, Subsecretaría de Educación. Provincia de Buenos Aires, Documento Nº 3.
Morellato, M. (2017). Travail coopératif entre professeurs et chercheurs dans le cadre d’une ingénierie didactique sur la construction des nombres: Conditions de la constitution de l’expérience collective.
Perrin, M., y Godin, M. (2018). Géométrie plane: Pour une approche cohérente du début de l’école a la fin du collège. HAL Archives-Ouvertes.
Sadovsky, P., Quaranta, M. E., García, P., Becerril, M. M., e Itzcovich, H. (2019). Trabajo colaborativo entre docentes e investigadores en didáctica de la matemática. Reflexiones metodológicas. UNRC., 26, 41-49.
SEP. (2017). Aprendizajes clave para la educación integral. Plan y programas de estudio para la educación básica.
