14. Relación entre procedimientos aritméticos de niños y las actividades familiares en las que participan

Mariela Medellín González*
Diana Solares-Pineda**
María del Carmen Ortiz Flores***

DOI: https://doi.org/10.52501/cc.132.14

Resumen

Esta investigación se propuso identificar procedimientos de cálculo aditivos y multiplicativos que utilizan nueve niños y una niña, entre 8 y 12 años de edad, en contextos de compra-venta. Se trata de una muestra de población infantil cuyas familias son comerciantes; la mayoría son migrantes de origen indígena. Mediante la indagación de prácticas comerciales de las familias, y con apoyo de la teoría de los campos conceptuales, se diseñaron e implementaron simulaciones de compra-venta para identificar los procedimientos de resolución de cada niño o niña. Con base en el concepto de participación periférica legítima se analizaron tales procedimientos considerando la participación que los menores tienen en las actividades laborales de sus familias. Se identificaron algunos vínculos entre los diversos procedimientos de resolución y el tipo de participación que los niños y la niña tienen en ese entorno familiar.

Palabras clave: menores trabajadores, conocimientos matemáticos, contexto de compra-venta, problemas aditivos, problemas multiplicativos, cálculo mental.

Introducción

Según encuestas oficiales de 2019, en México había 3 269 395 infantes y adolescentes de entre 5 y 17 años que realizaban algún tipo de actividad económica como vendedores. De ese conjunto, 1 755 528 efectuaban actividades laborales no permitidas, es decir, que de alguna manera los ponen en riesgo (Encuesta Nacional de Trabajo Infantil, 2019; en adelante, enti). En lo que concierne el estado de Querétaro, en 2017 la cantidad de menores trabajadores era de 25 720, de los cuales 82 % se desempeñaban en una ocupación no permitida (Secretaría del Trabajo y Previsión Social, 2017).

El comercio ambulante es una de las actividades no permitidas para menores de edad ya que están expuestos a temperaturas altas en las calles y a otras situaciones de riesgo (enti, 2019). Uno de los aspectos en que esa población se ve afectada es en su escolaridad, pues en muchos casos desertan de la escuela para apoyar económicamente a sus familias.

Como lo han documentado diversas investigaciones (Amezcua et al., 2020; Antonio, 2012; Galeana, 1997a, 1997b, entre otras), el trabajo infantil impacta fuertemente en la trayectoria escolar de niñas y niños. En su investigación denominada “La infancia desertora” realizada con niños trabajadores de zonas marginadas, Galeana (1997a) identifica una serie de antecedentes individuales y sociales que influyeron para el abandono de la escuela; se trata un proceso pluridimensional en el que confluyen aspectos económicos, familiares, culturales y afectivos.

La población infantil de la ciudad de Santiago de Querétaro que nos ocupa tiene la característica, además de ser trabajadora, de pertenecer a familias migrantes y, en su mayoría, indígenas. De acuerdo con Antonio (2012), la condición de migrante e indígena es un aspecto importante para la vulnerabilidad en la que se encuentran niños con esas características. En su estudio la autora analiza los factores que agudizan las desigualdades educativas de niños indígenas migrantes en una zona de la Ciudad de México. Identificó que muchas de las dificultades a las que se enfrentan son relativas a la lengua materna, pues tienen que aprender una segunda lengua para comprender aquello que la escuela enseña.

Por otra parte, los aprendizajes que niñas y niños trabajadores obtienen en sus actividades laborales no suelen ser reconocidos por la escuela. Galeana (1997b) plantea que en el ámbito laboral se genera un “ambiente de aprendizaje” y un “conocimiento psicosociocultural” que se adquiere mediante las redes e interacciones sociales; por ejemplo, aprender el lenguaje que se maneja en contextos de venta, o la manera de interactuar en determinados oficios y contextos laborales.

Las investigaciones antes mencionadas nos aportaron dos tipos de elementos: por una parte, sobre las condiciones económicas y sociales que han contribuido a la deserción escolar de esta población; por la otra, sobre la diversidad de aprendizajes que tienen lugar en los espacios extraescolares y en la que conviene poner atención.

En América Latina, y en México en particular, se han desarrollado investigaciones en torno a conocimientos matemáticos extraescolares propiciados por la actividad laboral de niñas, niños y adolescentes (Carraher et al., 1991; Padilla, 2015; Medellín, 2016 y 2020; Solares, 2012, entre otras). Esas investigaciones nos ofrecieron elementos para analizar los procedimientos aritméticos que se manifestaron en el presente estudio, así como para identificar relaciones entre esos procedimientos y las actividades específicas en las cuales se generan. Uno de nuestros intereses fue indagar cómo la incorporación gradual de niños y niñas trabajadores en las actividades laborales de sus familias podría manifestarse en sus recursos de cálculo.

Nuestro propósito es aportar elementos para la reflexión, la identificación de retos y problemáticas sobre las relaciones entre conocimientos matemáticos que tienen lugar en contextos escolares y extraescolares.

Partimos del estudio de Medellín (2016), quien, mediante entrevistas a niñas y niños vendedores, caracteriza prácticas de compra-venta de familias indígenas migrantes en la ciudad de Santiago de Querétaro. Posteriormente, retomamos hallazgos del estudio de Medellín (2020), quien recurre al diseño e implementación de simulaciones de compra-venta que implican problemas aditivos y multiplicativos. Destacamos dos aspectos de esos hallazgos: los procedimientos de cálculo utilizados por una niña y nueve niños, y las relaciones entre esos procedimientos y el tipo de participación que los infantes tienen en las actividades comerciales de sus familias. Por último, planteamos algunas reflexiones en torno a la metodología de investigación y a algunos retos para que la escuela reconozca y potencie los conocimientos matemáticos que niños y niñas han construido en el seno de la actividad laboral de sus familias.

Antecedentes

La importancia de los conocimientos matemáticos adquiridos en ambientes no escolarizados ha sido subrayada en distintos estudios. En Carraher et al. (1991) se reporta la manera en que resuelven problemas matemáticos niños trabajadores de Brasil, tanto en la escuela como fuera de ella. Los resultados obtenidos hablan de una discrepancia entre el desempeño en un contexto laboral y uno escolar, ya que a los participantes les resultó más sencillo resolver los problemas en situaciones reales de compra-venta que solucionar las mismas situaciones en el aula con el apoyo de lápiz y papel. Debido a lo anterior, los autores hablan de un fracaso escolar debido a:

a) la incapacidad de comprender la capacidad real del niño, b) un desconocimiento de los procesos naturales que llevan al niño a adquirir el conocimiento, c) la incapacidad de establecer un puente entre el conocimiento formal que se desea transmitir y el conocimiento práctico del cual el niño ya dispone. (Carraher et al., 1991, p. 45).

En su investigación, Solares (2012) identificó conocimientos matemáticos de niños y niñas migrantes que laboran, junto con sus familias, en un campo de cultivo. Para ello, caracterizó las actividades laborales del campo de cultivo que implican la lectura, la escritura y el cálculo numérico. A través de la simulación de algunas de esas actividades, la autora identificó en niñas y niños diversos conocimientos aritméticos. Solares (2012) plantea que tales conocimientos dependen de las finalidades de las actividades específicas, de los propósitos de los participantes y de los instrumentos que utilizan. Asimismo, indagó formas de comunicación de saberes entre trabajadores expertos y aprendices; particularmente de adultos expertos a niños o niñas aprendices.

Por su parte, Padilla (2015) exploró los conocimientos matemáticos de una niña y un niño en situaciones laborales que implican proporcionalidad. Presenta los casos de Inés, quien recolecta residuos para su venta, y de Ricardo, quien trabaja como albañil y repartidor de agua en pipas. La autora analiza las técnicas de resolución de cada participante y señala que éstas se encuentran determinadas por el contexto; plantea que las tareas de proporcionalidad están cargadas de significados matemáticos y sociales. Destaca, además, la importancia de las personas más expertas en el proceso de aprendizaje de los menos expertos.

Por último, la investigación de Medellín (2016), la cual es el antecedente inmediato del presente estudio, documenta los conocimientos aditivos de dos niñas vendedoras de la ciudad de Santiago de Querétaro. Su propósito fue aportar elementos que contribuyan a contrarrestar el rezago escolar de esta población, puesto que son escasos los servicios educativos que consideren la condición migrante de estas familias.

Al igual que en el estudio de Carraher et al. (1991), Medellín (2016) identificó que aun cuando las niñas enfrentaban un mismo tipo de problemas en el contexto escolar y en el laboral (composición de medidas y transformación de medidas), los procedimientos eran diferentes: en el contexto laboral usaban el cálculo mental, puesto que debían atender simultáneamente a varios clientes, mientras que en la escuela recurrían más a los algoritmos, por ser lo que la escuela demanda.

Medellín (2016) caracterizó las prácticas familiares en torno a la venta de productos en las calles. Advirtió que la variedad de productos, de precios y de dinero que los niños y las niñas de estas familias manejan cambia según la edad: las madres asignan a los de menor edad pocos productos para la venta, así como precios fijos de $5 o de $10, y no les dan monedas adicionales para dar cambio (la diferencia entre la suma total y el valor del billete o moneda con que se paga); por otro lado, a los de mayor edad les asignan una mayor diversidad de productos y precios, y sí reciben monedas para dar cambio.

Si bien la autora identificó esa organización familiar en torno a la venta, así como la diversidad de conocimientos matemáticos de las dos niñas participantes en su estudio, no se indagó cómo su participación diferenciada, según la edad, podría incidir en sus conocimientos matemáticos. Éste fue uno de los aspectos que posteriormente abordó la misma investigadora (Medellín, 2020), apoyándose en planteamientos teóricos de Lave y Wenger (2003), así como en la documentación de las interacciones entre expertos y aprendices de Solares (2012) y Padilla (2015).

Marco teórico y conceptual

Los referentes teóricos que sustentan las decisiones metodológicas de esta investigación están conformados por dos líneas: una que permitió comprender cómo ciertos aspectos sociales contribuyen en la conformación de conocimientos matemáticos de actividades específicas, y otra que orientó el diseño de situaciones exploratorias en torno a la resolución de problemas aditivos y multiplicativos.

Los conocimientos matemáticos en relación con las actividades humanas

La teoría del aprendizaje situado plantea que los conocimientos adquieren significado en las actividades cotidianas de los sujetos (Lave y Wenger, 2003); esta teoría destaca las relaciones entre el conocimiento y el entorno donde se produce; subraya que el aprendizaje no es producto de procesos cognoscitivos únicos, sino de cómo dichos procesos son conformados por la actividad y por las relaciones entre quien aprende y el entorno sociocultural de esa actividad (Sagastegui, 2004). Respecto al aprendizaje, estos autores enfatizan su papel “central e inseparable de la práctica social” (Lave y Wenger, 2003, p. 5).

En ese sentido, Medellín (2020) considera que los conocimientos matemáticos de niñas y niños vendedores tienen relación estrecha con las actividades de venta en las que participan y con el entorno donde se producen. Por ello, es indispensable comprender las actividades en las que los niños y las niñas participan junto con sus familias, así como identificar relaciones entre sus aprendizajes y las características sociales de esta población.

Lave y Wenger (2003) afirman que todas las comunidades tienen miembros que realizan prácticas de manera más experta que otros. Los menos expertos están en proceso de participar en la comunidad, es decir, gradualmente van pasando de una participación periférica a otra que está en el centro de la actividad. Para dar cuenta de ese proceso, los autores acuñaron el concepto de participación periférica legítima (en adelante ppl), el cual aborda las “relaciones entre novatos y veteranos y las relaciones entre las actividades, las identidades, los artefactos, las comunidades de conocimiento y las práctica” (Lave y Wenger, 1991, p. 3). La ppl es relevante en la concepción del aprendizaje como actividad situada, pues subraya la importancia de la participación para llegar a la adquisición de un conocimiento.

En la presente investigación la ppl permitió caracterizar la participación de cada uno de los niños en las actividades económicas de sus familias: algunos están al centro de la actividad de la venta, otros son observadores de la actividad y otros más están al margen de la misma. La teoría del aprendizaje situado y la ppl nos permitieron advertir, por ejemplo, que los más experimentados en la venta tuvieron mejores resultados en la resolución de problemas aritméticos que se les plantearon; sus procedimientos fueron más variados y algunas veces más económicos que otros, lo cual fue un hallazgo relevante de esta investigación.

Teoría de las situaciones didácticas (TSD)

La tsd está fundamentada en la noción de situación, la cual modeliza la interacción de un sujeto con el medio; dicha interacción determina la construcción del conocimiento matemático implicado.

La noción de medio es relevante en la tsd. Apoyándose en Brousseau (1986), Orús y Fregona (2011) la definen como “un sistema autónomo, antagonista del sujeto” (p. 26). Según Brousseau (2007), el alumno construye sus conocimientos mediante las interacciones que tiene con el medio, el cual abarca instrumentos, objetos, textos, material didáctico, consignas, restricciones, interacciones entre alumnos y demás elementos.

La tsd tuvo un papel fundamental en el presente estudio, pues una vez que se caracterizaron las actividades económicas en las que participan los niños, las niñas y sus familias, se diseñaron situaciones de compra-venta que provocaran ciertas interacciones entre los menores participantes y el medio, dando lugar a la manifestación de conocimientos matemáticos.

La situación exploratoria diseñada consideró la creación de un medio en el que los participantes actuaran autónomamente como vendedores y resolvieran problemas multiplicativos y aditivos propios del contexto de compra-venta con el que están familiarizados. Asimismo, se les solicitó que explicitaran los procedimientos utilizados para resolver tales problemas. Tanto los procedimientos correctos como los “errores” de los participantes fueron relevantes para este estudio, pues también los errores permiten identificar las concepciones de los sujetos sobre determinados conocimientos matemáticos (Brousseau, 2007).

Problemas aditivos y problemas multiplicativos

Dado que las actividades de compra-venta en las que participan niños y niñas de esta población implican operaciones aditivas y multiplicativas, fue necesario apoyarse en la tipología de problemas propuesta por Vergnaud, en el marco de la teoría de los campos conceptuales, tanto para analizar las actividades de compra-venta, como para diseñar ex profeso problemas aditivos y multiplicativos que exploraran los conocimientos de los participantes.

De acuerdo con Vergnaud (1991), los campos conceptuales de las estructuras aditivas y de las multiplicativas pueden caracterizarse: a) por el conjunto de situaciones que requieren determinadas operaciones para resolverse; b) por las relaciones y propiedades vinculadas a esas operaciones; c) por las formas de representar tales relaciones, propiedades y procedimientos de solución.

A las distintas formas en las que los datos de un problema se ponen en relación, Vergnaud (1991) las denomina “estructuras”. El autor identifica distintas categorías en los problemas de estructura aditiva, de las cuales se retomaron las siguientes para diseñar los problemas exploratorios: problemas de composición de medidas y problemas de transformación de medidas negativas (los ejemplos son de elaboración personal):

1. Problemas donde dos medidas se componen para dar lugar a otra medida. (“María compró un chicle de $3 y un mazapán de $5. ¿Cuánto gastó?”)
2. Problemas donde una transformación opera sobre una medida para dar lugar a otra medida. (“María compró dulces, fueron $8 y pagó con un billete de $20. ¿Cuánto recibió de cambio?”)

Las situaciones de compra-venta en las que participan los niños y las niñas vendedores coinciden con esas dos categorías.

En lo referente a los problemas de estructura multiplicativa, Vergnaud identifica dos categorías: isomorfismo de medidas y productos de medida. En este estudio se consideró la primera categoría por ser la más habitual en las situaciones de compra-venta. Esos problemas presentan una relación entre cuatro cantidades: dos son medidas de un tipo y las otras dos de otro tipo; tres medidas son conocidas y una desconocida. Su resolución implica una multiplicación. Por ejemplo: ¿Cuánto se cobrará por 5 paletas (medida de un tipo), si cada una cuesta $7 (medida de otro tipo)?

Cálculo mental

Como reportan investigaciones previas, la población infantil trabajadora suele recurrir a diversos procedimientos de cálculo mental para desarrollar sus actividades laborales.

Existe una discusión didáctica sobre semejanzas y diferencias entre procedimientos basados en algoritmos convencionales y los procedimientos de cálculo mental. Si bien se puede considerar que cualquier técnica que permita resolver operaciones matemáticas puede alcanzar un grado de automatismo como para considerarse un algoritmo, en este estudio nos apoyamos en el siguiente planteamiento de Vergnaud (1991) para distinguir el cálculo mental del algoritmo convencional:

Un algoritmo es una regla (o un conjunto de reglas) que permite, para todo problema de una clase dada con anterioridad, conducir a una solución, si existe una, o dado el caso, mostrar que no hay solución. Hay que subrayar que se puede decir que una regla “conduce a una solución” sólo si lo hace en un número finito de etapas; si este número no es finito, la regla podría aplicarse indefinidamente sin éxito. Ésta no sería, entonces, “efectiva”, y no sería un algoritmo (p. 258).

Para analizar los procedimientos de cálculo mental que manifestaron los participantes, nos apoyamos en Parra (1994), quien define al cálculo mental como un “conjunto de procedimientos que, analizando los datos por tratar, se articulan sin recurrir a un algoritmo preestablecido, para obtener resultados exactos o aproximados” (p. 222).

En un estudio de cálculo mental con niños mexicanos, Mochón y Vázquez (1995) identificaron diferentes procedimientos de estudiantes para resolver problemas aditivos, multiplicativos y operaciones aritméticas “puras”. Algunos procedimientos reconocidos por los autores son los siguientes: pasos de los algoritmos (aplicación mental del algoritmo escolarizado; no es una estrategia propiamente del cálculo mental), descomposiciones sencillas, redondeo más compensación, descomposición doble (se descomponen dos números y se opera con los números en común), compensación, ensayo y error. Cabe señalar que en la investigación de estos autores, los estudiantes que usaron algoritmos se equivocaron más que cuando usaron cálculo mental.

En coincidencia con algunos de los procedimientos anteriores, Gómez (1998) describe los siguientes procedimientos mentales aditivos, los cuales contribuyeron a describir los procedimientos identificados en este estudio:

• Descomponer uno de los términos para transformar la operación en una más cómoda.
• Alterar los términos de una operación para redondear a ceros.
• Descomposición y compensación: descomponer una cantidad para después añadir uno de los elementos que se descompuso. Por ejemplo: 57 + 38 = (57 – 2) + (38 + 2) = 55 + 40.
• Conteo ascendente y descendente.

Gómez, (1998) describe también diversos procedimientos multiplicativos, de los que se retoma la distribución: se trata de transformar uno o más factores en sumas o diferencias con el propósito de distribuir posteriormente los números. Por ejemplo: 8 × 42 = (8 × 40) + (8 × 2) = 320 + 16 = 336.

Como se verá más adelante, varios de los procedimientos mencionados se identificaron en el presente estudio. Cabe destacar que, como lo señala Parra (1994), la importancia del cálculo mental no radica únicamente en la resolución de problemas específicos, sino también en su contribución al establecimiento de relaciones numéricas.

Metodología

Se trata de un estudio cualitativo y con un alcance metodológico descriptivo-correlacional. Descriptivo porque, por un lado, busca “especificar las características y los perfiles de personas […] procesos o cualquier otro fenómeno que se someta a un análisis” (Sampieri, 2014 p. 98). En este caso se describen los procedimientos de cálculo mental utilizados por niños de familias vendedoras al resolver problemas de compra-venta. Y correlacional debido a que pretende “conocer la relación que existe entre dos o más variables de un contexto específico” (Sampieri, idem); en este caso, identificar las posibles relaciones entre los procedimientos de cálculo mental y la participación de los menores en las dinámicas laborales de las familias.

Población y muestra

Se incluyeron niños y niñas de origen indígena y cuyas familias participaran en actividades laborales de compra-venta. La decisión obedece a que esta población es la que comúnmente se dedica a la venta en las calles del Centro Histórico de Santiago de Querétaro, y porque ya se había tenido un acercamiento a ella en el estudio previo (Medellín, 2016). Otro criterio de inclusión fue que estuvieran cursando de tercero a sexto grado de primaria, debido a que en tercero inicia el estudio formal de problemas multiplicativos.

Como lo describe Medellín (2020), esta población se desenvuelve en “ambientes socio contextuales complejos”:

[…] se trata de niños que vemos en los semáforos vendiendo, que trabajan en los supermercados de “viene viene” (persona que apoya a los conductores para salir de un lugar de estacionamiento), que acompañan a sus padres a vender o simplemente a observar la actividad de venta. También son los niños que cuidan a sus hermanos más pequeños y que en ocasiones tienen que asumir roles de cuidadores, o que durante días no asisten a la escuela porque necesitan trabajar para apoyar en los gastos familiares, pues la misma subsistencia lo demanda. Son los niños que debido a sus condiciones de vida y dinámicas sociales tienden a abandonar la escuela, puesto que las prioridades se jerarquizan y, en este caso, la escuela no ocupa el primer lugar. (Medellín, 2020, p. 12)

La muestra estuvo conformada por nueve niños y una niña, quienes participan —en mayor o menor medida— en actividades laborales de compra-venta; sus edades oscilan entre los ocho y los doce años. Pertenecen a familias consideradas como “migrantes asentados”, es decir, si bien mantienen relaciones con sus comunidades de origen, pasan más tiempo en un lugar fijo la ciudad, generalmente en colonias que han sido marginadas de servicios públicos básicos, como agua, drenaje, alumbrado y seguridad.

Por las mañanas los 10 participantes asisten a una institución (Centro de Día) que les ofrece apoyo en tareas escolares, alimentación y cuidado; por las tardes van a la escuela primaria. El Centro de Día está ubicado en una zona considerada como “expulsora” de menores que trabajan en calles y cruceros de la ciudad (Boletín del Sistema Municipal para el Desarrollo Integral de la Familia, 2017); uno de los propósitos del Centro de Día es reducir la situación de riesgo en la que se encuentra esta población infantil.

Los participantes fueron contactados en un Centro de Día cuya población de niños, en ese momento, era superior a la de niñas, razón por la cual la muestra se conformó mayoritariamente por niños.

Para llevar a cabo el estudio se solicitó a las madres y los padres de familia su consentimiento, informándoles sobre los usos de los datos obtenidos y del compromiso de guardar la identidad de sus hijos y cuidar de su integridad durante el desarrollo del estudio. Los nombres que se usan en este escrito son seudónimos.

Técnicas

• Observación in situ: se hicieron observaciones de momentos laborales en los que se desenvuelven los niños, la niña y sus familias. La finalidad era ampliar la caracterización de prácticas de compra-venta identificadas por Medellín (2016).
• Observación participante: De acuerdo con Sampieri (2014), se trata de un instrumento de recolección de datos que implica estar presente durante reuniones, entrevistas en las que el observador puede participar realizando preguntas de manera abierta, lo que implica tener en cuenta la existencia del observador, su subjetividad y reciprocidad en el acto de observar. En esta investigación, al estar presente en algunos momentos laborales de las familias, cuando lo creía pertinente, la investigadora formulaba preguntas a los participantes para tener mayor claridad sobre la actividad en curso.
• Entrevista clínica: para profundizar en la comprensión de los procedimientos, se llevaron a cabo simulaciones de compra-venta en las que la investigadora, haciendo el papel de cliente, planteaba preguntas a cada participante para explorar más aún sus conocimientos.
• Entrevistas semiestructuradas: su propósito fue conocer la situación contextual de la niña y los niños, así como las dinámicas de venta en las que participan. Este tipo de entrevistas se hicieron también a sus madres o a sus padres.

Instrumento

El objetivo del instrumento fue identificar los procedimientos de resolución empleados por los niños y la niña al llevar a cabo la venta de dulces. Su diseño tuvo tres referentes: 1) las simulaciones de pago de deudas para explorar conocimientos matemáticos en menores trabajadores de un campo de cultivo, realizado por Solares (2012), a partir de la identificación del sistema de endeudamiento existente en campos de cultivo de México; 2) un instrumento diseñado por Solares, Ortiz y Bonilla (2016), en el cual se establecen roles del comprador (entrevistador) y del vendedor (estudiante), conocimientos matemáticos y sociales implicados en la compra-venta, variables didácticas y materiales por utilizar; 3) las indagaciones de Medellín (2016), quien observó in situ a menores al efectuar actividades de compra-venta; identificó qué productos vendían, costos, y dinámicas familiares en torno a la venta.

Con base en los referentes anteriores, se tuvo un acercamiento a las dinámicas laborales de las familias de los participantes y se recuperaron algunas de sus características para diseñar el instrumento de esta investigación (más adelante se describirán esas dinámicas).

El instrumento se conformó con cinco situaciones que simulaban actividades de compra-venta; cada situación incluía problemas con estructuras aditivas y multiplicativas, los cuales variaban en complejidad por el cálculo numérico y los números implicados. En la primera compra y en la segunda las cantidades eran múltiplos de cinco y diez, pero en la segunda se incluían precios cuya suma eran números redondos (10, 20, 30…); en la tercera compra se usaban precios similares a la segunda, pero aumentaba el número de productos; la cuarta incluía centavos; en la quinta se adquirían productos en paquete.

Al incluir esas características en cada una de las compras se pretendía mantener vínculos con la actividad observada en las calles (los productos y sus precios correspondían a los que suelen incluirse en las prácticas de compra-venta de dulces) y, al mismo tiempo, sostener el objetivo exploratorio de la simulación.

Los participantes jugaban el rol de “vendedor”, y la entrevistadora era la “compradora”. Esta decisión fue fundamental para indagar cómo la ppl de los niños y la niña se relacionaba con sus procedimientos de resolución y porque el rol de vendedores les lleva a efectuar acciones (cobrar y dar el cambio) que implican problemas aditivos y multiplicativos. Así, los participantes asumían mayores retos aritméticos, mientras que la entrevistadora podía ir tomando decisiones sobre las variables didácticas en juego e indagar con mayor profundidad los procedimientos de los menores.

Para los “vendedores” se puso a su disposición dulces y dinero real. También se les facilitó lápiz, papel y calculadora, por si querían utilizarlos; esto les daba mayores posibilidades de diversificar sus procedimientos.

Es conveniente señalar que este instrumento tiene alcances y limitaciones. Como advierte Solares (2012), las simulaciones favorecen la explicitación de conocimientos debido a que su diseño retoma actividades en las que participan los sujetos, lo cual puede resultarles significativo y, además, puede facilitarles la comprensión de las situaciones matemáticas que se plantean.

Por otro lado, con la finalidad de centrar la atención de los sujetos en ciertos aspectos numéricos, es inevitable −y necesario− alterar algunos rasgos de las actividades originales, lo cual podría ser una limitante. Otra limitante son los posibles efectos de ciertas expectativas de los participantes, como el usar procedimientos convencionales suponiendo que son los esperados por quien hace la entrevista.

Análisis a priori y análisis a posteriori

Una característica importante en la elaboración del instrumento fue que se hizo un análisis a priori (Artigue, 1995) para anticipar los posibles procedimientos correctos e incorrectos de los participantes.

Por ejemplo, para las distintas compras se previó la posibilidad de resolver contando de uno en uno, de tres en tres, de cinco en cinco, etc. Específicamente la tercera compra (se adquieren 7 cacahuates de $ 8.00 c/u, 3 botes de tamarindo de $ 8.00 c/u, 3 mazapanes de $4.50 c/u), en la cual se centra este capítulo, implicaba una multiplicación del número de productos por su precio respectivo, y se tenían previstas dos maneras de resolución: 1) que los participantes obtuvieran primero el total de los productos de $8 (cacahuates y tamarindos), y que el precio con centavos se descompusiera en enteros y decimales, para sumarlos por separado y luego obtener el total; 2) que consideraran los diez productos de $ 8 y multiplicaran de manera directa (10 × 8), para al final agregar de uno en uno el costo de los tres mazapanes. Esa anticipación se contrastó después con los procedimientos que realmente tuvieron lugar (análisis a posteriori).

Resultados

Las familias de los niños y de la niña se dedicaban a la venta de algún tipo de producto, entre ellos: recipientes de plástico, dulces, alimentos tradicionales (tortillas, gorditas), muñecas tradicionales, ropa, entre otros. Sobre todo eran las madres las encargadas de realizar esas ventas, y en algunos casos eran productoras de los mismos artículos. Respecto a los menores, no todos participaban necesariamente como vendedores, como se especificará más adelante.

Los rangos de precios que manejaban las familias eran diversos, dependiendo de los tipos de productos que vendían. En algunos casos el rango podía ir de $10 a $500, en otros entre $10 y $12; por ejemplo. Los precios también variaban si se vendía al menudeo o al mayoreo; había productos que se vendían por pieza, otros por paquete. Algunas de las familias ofrecían su mercancía de casa en casa, otras tenían puestos o lugares fijos para vender.

Se observó también que las madres de los participantes hacían las cuentas mentalmente para cobrar; no se advirtió que utilizaran la calculadora.

Si bien todas las familias se dedicaban a la venta de distintos productos, el tipo de participación de los menores era diferente. Con base en Wenger y Lave (2003), se categorizó el tipo de participación que los menores tenían: algunos estaban al centro de la actividad vendiendo productos; otros estaban presentes durante la venta observando cómo vendían sus progenitores y, en algunos casos, ayudando en la elaboración de los productos; otros más estaban al margen de la actividad, no participaban en la venta ni estaban como observadores de la misma. Esta diferenciación fue de suma importancia debido a que se identificó una relación entre la diversidad de procedimientos que manifestó cada menor y su tipo de participación en la actividad familiar.

Es importante precisar que esta categorización surgió en el desarrollo de la propia investigación. Inicialmente sólo se consideraba incluir a menores cuyas familias se dedicaran a la venta, asumiendo que los niños y las niñas de esas familias también participarían en esa actividad aunque no necesariamente de la misma manera que las personas adultas o expertas.

De los 10 menores, cuatro estaban al centro de la actividad y participaban de manera activa en la venta, tres eran observadores de la venta y tres estaban al margen de la actividad. Se advirtió que los procedimientos utilizados por quienes estaban al centro de la actividad eran más eficientes y diversificados que los usados por quienes estaban al margen de la actividad, como se advierte en la tabla 1.

Table 1. Procedimientos generales utilizados, según el tipo de participación de los menores

Compra	Características de la compra	Menores al centro de la actividad	Menores observadores de la actividad	Menores al margen de la actividad
Uno	Cinco tutsi pop de $5 c/u y dos bolsas de semillas de $10 c/u.	Composiciones, complemento aditivo, agrupaciones de 10 en 10.	Composiciones, complemento aditivo, agrupaciones de 10 en 10.	Composiciones, complemento aditivo, utilizaban los productos y monedas para el conteo, usaban los dedos.
Dos	Tres bolsas de semillas de $10 c/u, una caja de chicles de $12 y un pelón de $ 8.	Composición, descomposición, compensación, complemento aditivo.	Composición, descomposición, compensación, complemento aditivo, uso de dedos.	Utilizaban los productos y las monedas para el conteo, usaban los dedos, composición, descomposición, complemento aditivo.
Tres	Dos cajas de chicles de $12 c/u, siete cacahuates de $ 8 c/u, tres tamarindos de $ 8 c/u y tres mazapanes de $ 4.50 c/u.	Resultados parciales, composición, descomposición, compensación, redondeo, uso de lápiz y papel como recurso de apoyo, conocimiento de tablas de multiplicar, conteo con los dedos, redondeo, calculadora y complemento aditivo.	Resultados parciales, composición, descomposición, compensación, redondeo, uso de lápiz y papel, conocimiento de tablas de multiplicar, conteo con los dedos, redondeo, calculadora y complemento aditivo.	Registro escrito de lo contabilizado, descomposición, compensación, redondeo, uso de lápiz y papel, conteo con los dedos, calculadora, utilizaban los productos y las monedas para su conteo y complemento aditivo.
Cuatro	Tres paletas de $ 3.50 c/u, cuatro tamarrocas de $ 4.50 c/u, dos bolsas de semillas de 10 c/u, un tamarindo $10.	Composición, descomposición, compensación, redondeo, uso de lápiz y papel, resultados parciales, conteo con dedos y complemento aditivo.	Composición, descomposición, compensación, redondeo, uso de lápiz y papel, resultados parciales, conteo con dedos y complemento aditivo.	No concluyeron la resolución.
Cinco	Dos paquetes de cacahuates de $ 88 c/u, una caja de pulparindo de $ 38.50 y una bolsa de obleas de $ 38.50.	Composición, descomposición, redondeo, uso de lápiz y papel, calculadora, resultados parciales, composición, compensación y complemento aditivo.	Complemento aditivo, uso de lápiz y papel, redondeo y descomposición.	No concluyeron la resolución.

Fuente: Tomado de Medellín (2020, pp. 137-138).

En la misma tabla 1 se advierte que los procedimientos utilizados fueron cambiando y diversificándose dependiendo la compra y sus características. La compra tres presentó mayor diversidad de procedimientos, probablemente por el incremento de productos comprados. Debido a lo anterior sólo mostraremos de manera detallada dicha compra.

Puede inferirse que mientras mayor era el involucramiento de los menores en las actividades de venta de sus familias, sus cálculos eran desarrollados en mayor medida de manera mental y lograban dar una respuesta cercana o correcta al resultado, así como la conclusión de la compra. En cambio, quienes estaban al margen de la actividad de venta no concluyeron las últimas dos compras.

La compra tres dio lugar a una mayor diversidad de procedimientos debido, en buena parte, al número de productos que se adquirían y a los precios establecidos (alguno de ellos con centavos), como se muestran en la tabla 2.

Table 2. Costos y total de productos adquiridos en la tercera compra

Productos	Total de unidades que se compran	Costo por unidad	Total
Chicles Bolsas de cacahuates Bote de tamarindo Mazapanes	2 7 3 3	$12.00 $8.00 $8.00 $4.50	$24.00 $56.00 $24.00 $13.50
Total de la compra			$ 117.50

Nota: Se pagó con un billete de $100 y uno de $50, en total $150. Tomado de Medellín (2020, p. 96).

Análisis de las etapas de resolución implicadas en la tercera compra

Hacer el cobro del total de la compra y después dar el “cambio” implica hacer cálculos parciales, los cuales en este estudio se denominan “etapas”.

Los cálculos parciales podrían realizarse a través de seis etapas, como se muestra en la tabla 3. Para cada cálculo se representa, además, la solución canónica.

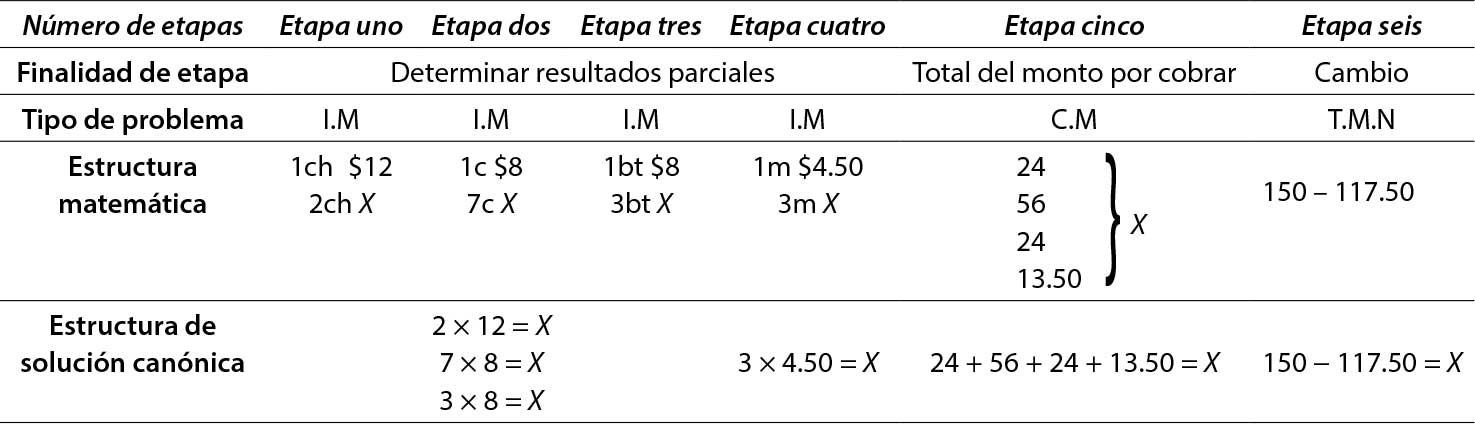
Nota: Las iniciales correspondientes al “Tipo de problema” son las siguientes: Isomorfismo de Medidas (I.M.), Composición de Medidas (C.M.) y Transformación de Medidas Negativas (T.M.N.). Y las letras en “Estructura matemática” se refieren a los productos que se compran: ch (chicles), c (cacahuates), bt (bote de tamarindo), m (mazapán). Tomado de Medellín (2020, p. 96).

Procedimientos utilizados en la tercera compra

En la tabla 4 se representan de manera general los procedimientos utilizados por los participantes para determinar el monto por cobrar.

Table 4. Procedimientos utilizados en la tercera compra, según el tipo de participación de los niños

Finalidad de procedimientos y validez del resultado	Procedimientos	Al centro de la actividad (4 niños de 10)	Observador de la actividad (3 niños de 10)	Al margen de la actividad (3 niños de 10)
Total por cobrar	Composición a números cómodos	4/10	1/10	0/10
	Resultados parciales	4/10	2/10	2/10
	Algoritmo de suma	1 /10	1/10	0/10
	Descomposición	3 /10	3/10	0/10
	Compensación	2/10	2/10	0/10
	Suma directa con calculadora	2/10	1/10	1/10
	Conteo de uno en uno utilizando los dedos	4/10	3/10	2/10
	Conteo con apoyo de monedas	0/10	0/10	1/10
	Apoyo en tablas de multiplicar	1/ 10	1 /10	0/10
	Redondeo	4/10	3 /10	0/10
Calcular el cambio	Complemento aditivo	4/10	2/10	1/10
	Complemento aditivo utilizando dedos	0/10	1/10	0/10
Alumnos que sí resuelven el problema o que se acercan al resultado		4/10	3/10	1/10

Fuente: Tomado de Medellín (2020, p. 98).

En esta compra puede observarse que quienes están al centro de la actividad y quienes son observadores de la actividad recurren sobre todo a la obtención de resultados parciales, al uso de las tablas de multiplicar, a procedimientos como la descomposición, la compensación y el redondeo; a diferencia de quienes están al margen de la actividad que recurren al apoyo de las monedas y al uso de dedos para hacer conteos. Se observa, además, que quienes están al margen de la actividad no pudieron concluir sus cálculos. Cabe aclarar que un solo participante pudo haber utilizado distintos procedimientos en las diferentes etapas de la compra.

Respecto a los procedimientos para determinar el cambio, se identificó el complemento aditivo y el apoyo de dedos. Estos procedimientos se presentaron en todas las compras.

Los resultados anteriores dan cuenta de una posible relación entre el tipo de participación (ppl) y los procedimientos que los menores ponen en juego al resolver la situación: el bagaje de procedimientos es más amplio para los niños que se encuentran en el centro de actividades de compra-venta. Además, para ese tipo de participantes como para quienes se encuentran como observadores de la actividad, el rango de aciertos es mucho mayor que quienes se encuentran al margen de la actividad.

Descripción de algunos procedimientos para calcular cuánto cobrar

A continuación, recurrimos a las categorías empleadas por Gómez (1998) para describir algunos de los procedimientos utilizados al momento de cobrar. Se reporta el número de participantes que los emplearon, y se presentan algunos ejemplos.

Conteo. Fue utilizado por 9 de 10 participantes y se manifestó de dos formas: el conteo de monedas y el conteo de uno en uno recurriendo a los dedos. Estos procedimientos se advirtieron en las tres primeras etapas de resolución (cálculo de resultados parciales) de la compra, en las cuales los problemas multiplicativos son de tipo isomorfismo de medidas (im); también se advirtió en la etapa cinco en la que se determina el monto por cobrar.

Fuente: Tomado de Medellín (2020, p. 102).

El conteo con monedas lo usó 1 de los 10 participantes, quien se ubicaba al margen de la actividad y establecía una relación entre el costo de cada producto y las monedas que le correspondían, para después contar todas las monedas de todos los productos (figura 1).

El conteo con los dedos fue utilizado por 9 de los 10 participantes: cuatro al centro de la actividad, tres observadores de la actividad y dos al margen de la actividad. Cabe precisar que este tipo de conteo se usó junto con otros procedimientos; por ejemplo, en la figura 2 se muestra la representación que hizo Carlitos de las sumas iteradas de algunas cantidades (8, 4.50 y 12), las cuales resolvió apoyándose en el conteo de dedos uno a uno.

Figura 2. Resolución de sumas iteradas de cantidades apoyándose en el conteo uno a uno con ayuda de dedos

Fuente: Tomado de Medellín (2020, p. 108).

Algoritmo. 6 de 10 participantes usaron el algoritmo de la suma ya sea para obtener resultados parciales o para obtener el monto total de lo que debía cobrarse. En algunos casos el algoritmo se utilizó de manera “híbrida” con otros procedimientos. Por ejemplo, 2 niños cuya participación estaba al centro de la actividad, obtenían resultados parciales mediante cálculo mental, los registraban y después hacían el algoritmo de la suma para obtener el total. Es el caso de Jesús, quien para calcular el total de siete bolsas de cacahuates ($8 cada una), obtiene por cálculo mental lo correspondiente a dos bolsas ($16); registra tres veces esa cantidad para representar seis bolsas y obtiene $48. Después agrega $8 de la séptima bolsa. Posteriormente registra tres veces $8, que corresponden a los tres botes de tamarindo. Se puede advertir que marca dos de los 8 y escribe frente a ellos 16, que es otro resultado parcial, probablemente apoyándose en el cálculo que previamente hizo para dos bolsas de cacahuates. Al final utiliza el algoritmo de la suma para determinar el total del costo (80) de los dulces que hasta ese momento ha considerado (figura 3).

Figura 3. Algoritmo de la adición utilizando resultados parciales

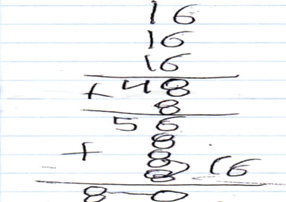
Fuente: Tomado de Medellín (2020, p. 105).

Apoyo en tablas de multiplicar. Este procedimiento fue utilizado por 2 de 10 participantes, uno al centro de la actividad y el otro observador de la actividad. Se manifestó en las etapas 2 y 3, en las cuales hay varios productos cuyo precio es $8 y el problema es de tipo isomorfismo de medidas. En el siguiente ejemplo se aprecia cómo Ángel (A) se apoya en las tablas de multiplicación y en el cálculo mental para obtener un total.

Uso de calculadora. Para obtener el monto total de la compra, 4 de 10 participantes recurrieron a la calculadora: 2 al centro de la actividad de venta, 1 observador y 1 al margen de la actividad. Se identificaron dos formas de usar este recurso: la primera consistió en sumar los resultados parciales obtenidos mediante otros procedimientos (entre ellos el cálculo mental), y la segunda fue ir registrando en la calculadora el costo de cada producto.

Descripción de procedimientos para calcular el cambio

Este cálculo tiene lugar en la etapa 6 en donde se propone un problema de tipo transformación de medidas negativa (tmn) y el principal procedimiento utilizado para obtener la diferencia entre el valor del billete con el que se paga y el monto del cobro fue calcular el complemento aditivo, el cual consiste en partir del sustraendo e ir añadiendo lo necesario hasta llegar al minuendo. La cantidad agregada es esa diferencia. La búsqueda del complemento aditivo se apoyó en el conteo oral y, en algunos casos, en el uso de monedas o de los dedos.

En el siguiente ejemplo, Ramón (R) explica cómo parte del total hasta llegar al monto con el que se pagó (se muestra con subrayado). Llama la atención que, a diferencia de los demás entrevistados, Ramón reconoce la resta como la operación que está implicada en el problema, y la resuelve mediante el complemento aditivo:

Recordemos que el total por cobrar fue de $ 117.50 y le pagaron con un billete de $ 100.00 y otro de $ 50.00 ($ 150.00).

Contraste entre los procedimientos esperados y los que se presentaron (análisis a posteriori)

Nos centraremos en los procedimientos no esperados. En el análisis previo no se consideró que los participantes pudieran recurrir al conteo utilizando monedas ni estableciendo una correlación entre el costo de los productos y las monedas, lo cual resultó recurrente sobre todo en quienes participan como observadores de la actividad. Tampoco se tenía considerado el uso “híbrido” del algoritmo de la suma, ni la obtención de resultados parciales por cálculo mental al tiempo que había apoyo en la escritura.

Para dar el cambio, hubo participantes que también recurrieron al algoritmo, el cual no era esperado debido a que se ha documentado la escasa o nula relación que establecen estudiantes de primaria entre la operación “resta” y la búsqueda de una diferencia (Medellín, 2020).

Un último aspecto por destacar es que a partir de la tercera compra se identificó una mayor diversidad de procedimientos en quienes están al centro de la actividad y en quienes son observadores de la actividad; mientras que quienes están al margen tuvieron más dificultades para resolver el problema. Es importante señalar que la diversidad de procedimientos se amplió al incrementar los rangos numéricos y la cantidad de productos.

De acuerdo con las observaciones realizadas in situ, inferimos que algunos de los procedimientos presentados están vinculados con las prácticas de venta de las familias: las madres de los participantes realizaban sus cálculos de manera mental; no se observó que usaran calculadora ni que se apoyaran en sus dedos. El cálculo mental también se manifestó en los participantes ubicados al centro de la actividad y en quienes sólo eran observadores de la misma, pues aun cuando usaban los dedos como apoyo y de manera casi oculta, al igual que sus madres no tardaban mucho en dar sus resultados. En cambio, a quienes se encontraban al margen de la actividad no les preocupaba hacer visible la utilización de los dedos o hacer conteo de uno en uno, ni tardar en dar una solución.

El análisis de los procedimientos muestra que las variables didácticas consideradas en el diseño de las simulaciones efectivamente provocaron que los participantes manifestaran sus conocimientos matemáticos, especialmente cuando se daban cuenta de que un procedimiento no funcionaba y recurrían a otro.

Discusión

Los resultados de esta investigación tienen similitudes con algunos hallazgos de estudios sobre poblaciones en situaciones de vulnerabilidad, los cuales fueron comentados en el apartado de Antecedentes (Block y Dávila, 1993; Carraher el al.,1991; Galeana, 1997a y 1997b; Padilla, 2015; Solares, 2012; Medellín, 2016), particularmente en lo que se refiere al uso de procedimientos no convencionales que resultan más comprensibles para las niñas y los niños, en comparación con los algoritmos.

La diversidad de procedimientos que se manifestó hace evidente la pertinencia del contexto de compra-venta en la movilización de ciertos conocimientos matemáticos de esta población infantil. Por supuesto, la expresión de esa diversidad no sólo es atribuible al contexto sino también al diseño de cada una de las situaciones exploratorias, a los rangos numéricos elegidos y a las relaciones que se establecieron entre los datos. Por ejemplo, es posible advertir cómo algunos procedimientos iban siendo cada vez más complejos en función de las características y la dificultad de las mismas situaciones planteadas, de manera tal que algunos participantes transitaron de las sumas iteradas al uso de tablas de multiplicar, por mencionar un caso.

Asimismo, fue relevante en el repertorio de procedimientos de los menores el tipo de participación que tienen en las actividades de venta de sus familias, por lo que consideramos que podría existir una correlación entre esa participación y los conocimientos matemáticos que se manifestaron: los procedimientos de resolución parecen ser independientes de la edad y grado escolar, pues había niños de menor edad y escolaridad cuyos procedimientos fueron más eficientes que los de niños de mayor edad y escolaridad, al parecer por el hecho de que los primeros estaban al centro de la actividad laboral de sus familias, mientras los segundos estaban al margen de actividades laborales.

Por otra parte, los menores que son observadores de la actividad utilizaron recursos muy similares a los que usan quienes están al centro de la actividad, aun cuando su participación como vendedores es más limitada. Las diferencias fueron sutiles, sobre todo en la rapidez con la que efectúan los cálculos.

Otra diferencia relevante entre los tipos de participaciones, fue que quienes están al centro de la actividad lograban verbalizar con mayor facilidad sus procedimientos y dar justificaciones sobre los mismos durante las entrevistas. Si como lo plantean Chaiklin y Lave (2001), desde la perspectiva del aprendizaje situado los aprendizajes resultan de las relaciones entre quien aprende y su entorno social y cultural, resta por indagar si esa verbalización es resultado de técnicas de cálculo empleadas y enseñadas por sus progenitores en el contexto del trabajo familiar, o si es resultado de aprendizajes escolares. O incluso una fusión de ambas fuentes de aprendizaje.

El que la escuela valore y aproveche los conocimientos matemáticos que esta población ha construido a partir de sus experiencias extraescolares podría contribuir en la disminución del abandono escolar. La utilización de recursos no necesariamente canónicos, generalmente excluidos en el ámbito escolar, podría aportar elementos para el aprendizaje de conocimientos propiamente escolares. Por ejemplo, las descomposiciones y composiciones de cantidades tienen relación con propiedades del sistema de numeración decimal, las cuales pueden hacerse explícitas desde la escuela. Asimismo, la escuela puede contribuir al desarrollo de procedimientos de cálculo mental sistematizando su estudio y diversificando las técnicas. Y en lo que respecta a las operaciones básicas, es en el espacio escolar donde las niñas y los niños pueden ampliar también los significados de esas operaciones, por ejemplo, que la resta no sólo ayuda a resolver problemas en los que “se quita” una cantidad, sino también aquellos en los que se busca calcular una diferencia, como es el caso de calcular “el cambio” en las actividades de compra-venta.

Reflexiones finales

La experiencia obtenida durante el desarrollo de este estudio, así como los resultados del mismo, constatan la necesidad de un “cruce de miradas” teóricas y metodológicas para abordar problemáticas complejas. Como lo señala Medellín (2020), es necesaria una indagación y comprensión de las actividades que desarrollan los sujetos al interior de una comunidad determinada, en este caso, la actividad laboral de la familia, para advertir los conocimientos matemáticos presentes en el desarrollo de esa actividad específica, sus usos y los significados que adquieren en ese contexto. Es ahí donde la perspectiva didáctica tiene un papel fundamental: la comprensión profunda del funcionamiento de un determinado conocimiento matemático, los tipos de problemas que ese conocimiento matemático permite resolver, la diversidad de procedimientos de resolución que tienen lugar, los alcances y limitaciones de los mismos.

Ese cruce de miradas tiene varios retos aún que enfrentar, particularmente en el plano metodológico. Como lo advierte Solares (2012), ¿cómo plantear situaciones problemáticas a través de las simulaciones “[…] manteniendo, por un lado, los elementos que le dan veracidad a la situación y, por otro lado, haciendo las adecuaciones necesarias para indagar los conocimientos matemáticos que […] interesan”? (pp. 110-111).

Los anteriores son retos y alternativas para la investigación. Para la enseñanza escolarizada se advierten otros tal vez más complejos que, si bien no son nuevos, sí interpelan aún más a la escuela ante el aumento del rezago escolar generado por la reciente pandemia por covid-19, el desempleo, la creciente precarización y migración de las poblaciones rurales hacia las ciudades. ¿Cómo concretar propuestas educativas que permitan reconocer y promover el cálculo mental y otros procedimientos no convencionales en el aula?, ¿cómo hacer más visibles tales conocimientos en los espacios curriculares?, ¿cómo crear puentes entre lo que los niños aprenden de conocimientos matemáticos más allá de la escuela y lo que se debe enseñar en ella? Al respecto, vale la pena enfatizar que los conocimientos matemáticos en torno a los problemas aritméticos aditivos y multiplicativos son considerados fundamentales en el currículo de la educación básica, de ahí la necesidad de estas reflexiones desde la escuela.

Esta investigación hace evidente la importancia del cálculo mental para los niños que participan, en mayor o menor medida, en actividades de compra-venta junto con sus familias; asimismo, insiste en lo que investigaciones previas han mostrado: la discrepancia entre el uso forzado de algoritmos al interior del salón de clases y las dificultades que esto conlleva, y el poco aprovechamiento que tiene el cálculo mental más allá del salón. Uno de los tantos retos escolares es cómo incluir prácticas de cálculo mental que potencien ese conocimiento y que sean un medio para comprender las relaciones, regularidades y propiedades numéricas del sistema de numeración. Otro más es cómo valorar y socializar los conocimientos matemáticos que ya los niños y las niñas han construido más allá de la escuela, acrecentando así su bagaje de soluciones.

El presente estudio pretende aportar elementos para futuras propuestas didácticas; uno de esos elementos es el diseño de distintos problemas aditivos y multiplicativos que, a partir de una misma situación de compra-venta, pueden generar una diversidad de procedimientos como consecuencia de la modificación de ciertas variables didácticas, las cuales han sido identificadas en actividades propias de las familias trabajadoras. Como se ha comentado, sigue quedando pendiente, por otro lado, profundizar en la indagación de cómo las familias trabajadoras comparten entre sus miembros los conocimientos y las estrategias generados desde sus actividades específicas.

---

Bibliografía