13. Conocimientos matemáticos de menores trabajadores: Una mirada a través de la proporcionalidad y la pepena

Erika Isabel Padilla Carrill0*
Armando Solares-Rojas**

DOI: https://doi.org/10.52501/cc.132.13

Resumen

En este capítulo estudiamos conocimientos matemáticos que niños trabajadores ponen en juego al enfrentar situaciones de proporcionalidad presentes en sus actividades laborales. Para ello, recurrimos a herramientas teóricas y metodológicas del campo de la didáctica de las matemáticas, la etnografía y el aprendizaje situado. Encontramos que los menores trabajadores enfrentan tareas matemáticas ricas y complejas, tanto por las restricciones provenientes de los contextos en que se presentan estas tareas como por sus características matemáticas y las técnicas que los niños usan para resolverlas. Nos enfocamos en el análisis de la actividad laboral de Isabel, miembro de una familia que (sobre)vive de la pepena de cartón. Realizamos observaciones in situ de su actividad y una entrevista fuera de su lugar de trabajo. Esperamos que los resultados que presentamos sean de utilidad para construir puentes entre los conocimientos matemáticos que los menores trabajadores estudian en la escuela y los que movilizan en su entorno laboral.

Palabras clave: conocimientos matemáticos, menores trabajadores, proporcionalidad, técnicas y tareas matemáticas.

Introducción

Cuando llevaba tres años como maestra de primaria, vi a Isabel por primera vez, llegó al salón de clases de primer grado. Era una niña menuda de cabello enmarañado y cierta dificultad para hablar. Fui su maestra por dos años, pero durante ese tiempo no supe que ella, junto a su madre, trabajaba en la pepena de cartón en un basurero, como ya lo venía haciendo años atrás. Su ausencia en el salón de clases era frecuente, fue difícil que aprendiera a leer y escribir, aunque era evidente su facilidad para los números. Siendo maestra estaba acostumbrada a vivir situaciones diversas, pero ni el conocimiento ni la intuición alcanzaron para advertir y asumir las formas sutiles del trabajo infantil que tenía delante.

Relato de una experiencia de la primera autora

como maestra frente a grupo en el año 2009.

Son muchos los momentos significativos que algunos profesores experimentan al llegar a sus centros escolares por vez primera y que continúan viviendo en el transcurso de los siguientes años. Cuando se habla de contextos sociales marginados o vulnerables, dichas vivencias pueden convertirse en experiencias de vida que marcan la perspectiva de la educación que se tiene. En estos contextos se podrían mencionar cientos de situaciones donde es posible identificar las urgentes necesidades de niños y niñas que no cuentan con la disponibilidad ni el acceso a una educación y vida dignas —premisas fundamentales si pretendemos valorar, fortalecer y respetar los derechos fundamentales de la infancia, tan constantemente vulnerada—. Muchos de ellos son protagonistas de historias de pobreza, abandono, descuido, que los llevan a trabajar desde niños, mientras intentan también mantenerse en la escuela.

Indudablemente los menores trabajadores están inmersos en un sistema educativo que desdibuja el trabajo infantil. De acuerdo con el inegi (inegi, 2009), en la Zona Metropolitana del Valle de México³⁰ hay más de 370 000 menores trabajadores. Muchos de estos niños trabajadores estudian y trabajan. Pero, como señala Galeana (1997), la sociedad y las instituciones escolares muestran una “aparente ignorancia” ante esta situación. Los menores trabajadores parecen “inexistentes”, reconocidos en la escuela más como “alumnos” que como sujetos sociales con historia propia.

Combinar trabajo y escuela lleva, en numerosas ocasiones, a estos niños a asistir de manera irregular a la escuela; incluso muchos de ellos están en riesgo de deserción escolar. Pero la investigación educativa ha detectado que estos niños son altamente competentes en el uso de ciertos conocimientos que ponen en juego en su trabajo y —en ocasiones— en la escuela. Entre éstos destacan los conocimientos matemáticos que les demanda su actividad laboral y que, al mismo tiempo, con significados y usos propios, circulan en su ámbito escolar. El estudio que presentamos tiene por objetivo identificar y analizar maneras en que los niños trabajadores usan sus conocimientos matemáticos en sus actividades laborales. Focalizamos nuestra atención en Isabel, una niña recolectora de cartón. Mostraremos la complejidad de las situaciones y los conocimientos matemáticos a los que suele enfrentarse en su actividad laboral, las maneras en que su actividad “da forma” a estos conocimientos, así como las interrogantes que surgen para la escuela y la educación matemática.³¹ Si bien nos restringimos a los contextos laborales y no mostramos un diseño educativo para la escuela, esperamos que los resultados que presentamos contribuyan a la construcción de puentes y articulaciones didácticos entre los conocimientos matemáticos que los menores estudian en sus salones de clases y aquellos que construyen en sus actividades laborales.

Consideramos que este estudio puede ser de interés para investigadores en didáctica de las matemáticas, maestros y diseñadores de currículo. Los invitamos a poner la mirada en aquello que en ocasiones no se mira: la riqueza de los conocimientos de los menores trabajadores, pero sin dejar de lado sus historias de vida y las situaciones de marginación y pobreza que enfrentan. Consideramos necesario hablar de las tareas matemáticas que enfrentan y cómo las resuelven, pero también de las maneras en que las restricciones de su contexto dan forma a esas tareas, a sus técnicas y a sus conocimientos.

Nos interesa sobremanera compartir nuestros hallazgos con quienes se encuentran diariamente en los salones de clases con niños y niñas que trabajan: maestras y maestros. Esperamos que aprendamos a reconocer a estos niños y niñas, que aprendamos a ver más allá de las paredes impuestas por la escuela, que reconozcamos sus historias de vida, sus sentires y —también— sus conocimientos matemáticos. Confiamos en que, al ir leyendo este capítulo, se vayan haciendo visibles los menores que trabajan y que están en nuestras aulas.

¿Por qué la proporcionalidad?: la vida y las actividades de los menores trabajadores de este estudio

Como lo señalan numerosas investigaciones, las actividades laborales constituyen espacios en los que los menores trabajadores tienen frecuentemente relación con la proporcionalidad (Carraher et al., 1995; Lave, 1991; Soto, 2001; Ávila, 2009; Solares, 2012; Padilla, 2015; Padilla y Solares-Rojas, 2013). Nuestras observaciones iniciales de la actividad laboral de los menores confirmaron la presencia habitual de la proporcionalidad; por ejemplo, al observar la labor de Gonzalo, vendedor de “aguas frescas” de 12 años de edad, encontramos el siguiente diálogo con uno de sus clientes.

Gonzalo se enfrenta a una situación matemática que le demanda la solución de dos tipos de tareas: una de tipo multiplicativo y la otra de tipo aditivo (Vergnaud, 1991). Obtener el resultado correcto de la primera le permitirá tener éxito en la segunda (y evitar perder dinero en la venta).

Para resolver la primera tarea, Gonzalo no pone en marcha una técnica en la que aparezca de manera explícita el algoritmo de la multiplicación, la división o la regla de tres; la situación matemática a la que se enfrenta desencadena la siguiente técnica “no canónica”: Gonzalo agrupa números de aguas: dos (aguas) son 30 (pesos), más dos (aguas) 60 (pesos) y 15 (pesos del agua de limón con chía) son 75 (pesos en total). Podemos decir que la aplicación de esta técnica involucra una relación de proporcionalidad entre dos magnitudes de diferente naturaleza: por un lado, el número de aguas y, por el otro, el costo. Las cuatro cantidades³² puestas en relación se pueden expresar mediante el siguiente esquema (tabla 1), en el que se busca la incógnita —la cuarta proporcional— que corresponde al costo de cinco aguas.

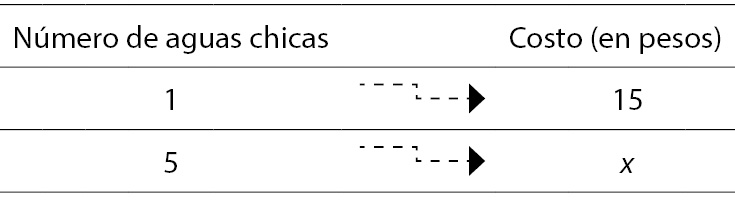
Para resolver esta tarea, Gonzalo va relacionando de manera alternada ambas magnitudes: dos aguas son $30, más dos (cuatro aguas) son $60, y si un agua es $15, entonces, cinco aguas son $75. Recurriendo a nuestras herramientas de análisis, podemos decir que al aplicar esta técnica Gonzalo hace uso de la propiedad aditiva de la proporcionalidad,³³ en cada paso, al considerar que el costo de 5 aguas se puede calcular al sumar el costo de 2 aguas³⁴ más el costo de otras 2 aguas más el costo de 1 agua, es decir, $30 + $ 30 + $ 15, que es igual a $75.

Una vez resuelta la tarea de calcular cuánto debe cobrar al cliente por las cinco aguas, Gonzalo enfrenta la segunda tarea: determinar cuánto debe dar de cambio al cliente. La solución que da Gonzalo puede describirse a partir del procedimiento del complemento, que consiste “en buscar, sin hacer una sustracción, lo que hay que añadir (o quitar) al estado inicial para llegar al estado final” (Vergnaud, 1991, p. 172).

El ejemplo de Gonzalo es sólo una muestra de la enorme cantidad y la muy variada naturaleza de los conocimientos matemáticos que pueden identificarse al considerar la actividad laboral cotidiana de los menores trabajadores: vendedores de agua potable, meseros, chalanes de albañil, pepenadores y muchos más. En este capítulo buscamos escuchar y compartir las historias, las voces y los conocimientos de niñas y niños que son muchas veces ignorados por el sistema educativo. Exploramos respuestas a la pregunta: ¿qué conocimientos matemáticos ponen en juego los menores trabajadores para resolver las situaciones de proporcionalidad que les demanda su actividad laboral? Para responderla, identificamos tareas que los menores enfrentan en su trabajo y, a partir de ellas, analizamos los conocimientos matemáticos que movilizan para resolver específicamente tareas de proporcionalidad, considerando las restricciones y características de su actividad laboral.

Antecedentes y marco de referencia

El estudio de los conocimientos matemáticos con poblaciones específicas, en contextos laborales y de la vida cotidiana, con adultos no alfabetizados, niños trabajadores y poblaciones marginalizadas, en general, ha sido ampliamente documentado por la investigación en educación matemática (Carraher et al., 1995; Lave, 1991, 2011; Soto, 2001; De Agüero, 2006; Fuenlabrada y Delprato, 2005; Ávila, 2009; Kalman y Solares 2018; Solares 2011, 2012; Padilla, 2015; Padilla y Solares-Rojas, 2013; Solares et al., 2016; Rogoff, 1990; Traoré y Bednarz, 2009).

Algunas de estas investigaciones destacan las diferencias, contradicciones y dificultades para conectar el aula con contextos extraescolares (por ejemplo, Carraher et al., 1995; Lave, 1991, 2011). En su investigación con niños vendedores ambulantes de Brasil, Carraher y colaboradores identificaron que los métodos extraescolares no eran reconocidos por la escuela, a pesar de ser correctos y de ser —en cierto modo— más eficientes que los escolares. Sobre esta base, estos autores cuestionan los ideales de la escuela y ponen a discusión el rol de ésta en el fracaso escolar de niños provenientes de los sectores más pobres de la población. Por su parte, Lave (1991, 2011) y Rogoff (1990) introdujeron la noción de aprendizaje de las matemáticas como un producto de prácticas socialmente situadas. Lave afirma que las prácticas matemáticas en la vida diaria son poderosas y que las personas trabajan con las matemáticas de una manera diferente a las situaciones escolares, independientemente de haber asistido o no a la escuela. Lave concluye cuestionando la efectividad de las prácticas escolares en la integración de experiencias extraescolares.

Por otra parte, la literatura en etnomatemática (D’Ambrosio, 2002) y educación matemática crítica (Skovsmose y Valero, 2009) han puesto en evidencia y discutido la relación asimétrica entre las matemáticas de las poblaciones marginales locales y las matemáticas de la escuela, considerando como una imposición cultural la introducción de estas últimas (D’Ambrosio, 2002; Geistera, 2001; Knijnik, 2003). Por ejemplo, Soto (2001) señala la distancia entre los programas educativos y los conocimientos involucrados en los procedimientos que utilizan los campesinos chilenos para resolver problemas laborales. Esta autora concluye que los contextos más pobres de las zonas rurales y urbanas tienen los rendimientos matemáticos más bajos porque el currículo homogeneiza la cultura escolar.

Otros estudios han analizado los procesos de circulación del conocimiento matemático entre distintos contextos e instituciones (Hoyles et al., 2010; Castela y Elguero, 2013; Castela, 2016, 2019). Sin embargo, a pesar de que varias investigaciones recientes han buscado integrar en la escuela otras formas de conocimientos matemáticos desarrollados fuera de la escuela (Kisker et al., 2012; Lipka et al., 2019; Stathopoulou, 2017; Pradhan, 2017; Sharma y Orey, 2017; Albanese et al., 2017; Das Graças y Marinho, 2015; Verner et al., 2019; Solares y Block, 2021), aún se sabe poco sobre propuestas educativas concretas para hacerlo en los salones de clases. Esta integración no es sencilla, ya que se encuentra sumergida en una compleja red de continuidades y discontinuidades entre los saberes propios de las instituciones educativas y los de las otras instituciones, grupos culturales y contextos (Solares et al., 2016; Trinick et al., 2017). El estudio que presentamos a continuación se suma a los esfuerzos por construir puentes entre los conocimientos matemáticos que los niños desarrollan fuera de la escuela —y específicamente en sus actividades laborales— y las matemáticas de los salones de clases.

Marco de referencia: nuestra mirada para este estudio

Para acceder y analizar los conocimientos matemáticos provenientes de las actividades laborales cotidianas de los menores, recurrimos a algunas herramientas teóricas provenientes de los estudios etnográficos de la Cognición en la práctica (Lave, 1991, 2011).

Para Lave, las actividades sociales, y en especial las laborales, involucran escencialmente la cognición. En sus propias palabras:

No se trata de que la distribución del conocimiento en el cerebro se corresponda de forma complicada con el mundo social externo a él, sino de que está organizada socialmente de forma que resulta indivisible. La “cognición” observada en la práctica cotidiana se distribuye —desplegándose, no dividiéndose— entre la mente, el cuerpo, la actividad y los entornos organizados culturalmente (que incluyen a otros actores). (Lave, 1991, p. 17).

Para ella, además de las propiedades matemáticas formales, “hay otros factores en la situación que conforman los problemas: las actividades en progreso, la estructura del entorno y sus relaciones” (Lave, 1991, p. 117). En el presente estudio, la perspectiva de Lave nos permite estudiar la relación entre el conocimiento matemático y la actividad concreta “situada”, posibilitando identificar las maneras en que el conocimiento matemático toma forma y significado, bajo las relaciones sociales y con las restricciones de la actividad laboral.

Para analizar cómo la realización de las actividades da forma y sentido a las relaciones matemáticas, específicamente las cuantitativas, Lave introduce el concepto de recursos de estructuración (Lave, 1991). Por ejemplo, en la realización de la compra diaria, los cálculos que hace la gente constituyen un recurso de estructuración para el proceso de la compra; a su vez, la compra aporta recursos de estructuración que dan forma, significado y puntualizan el proceso de hacer cálculos. En la práctica, la compra y el hacer cálculos se conforman mutuamente.

Lave señala que “en la práctica, tales recursos [los recursos de estructuración] no sólo se encuentran en la memoria de las personas, sino en la propia actividad, en relación con el entorno, tomando forma a partir de la intersección de múltiples realidades, producidos en conflicto y generando valores” (Lave, 1991, p. 114). Otros posibles recursos de estructuración están dados por los sistemas monetarios que median las transacciones comerciales, por ejemplo.

Por otra parte, siguiendo los planteamientos de la teoría antropológica de lo didáctico, o tad (Chevallard, 1999), asumimos que el identificar los tipos de tareas y técnicas de la actividad laboral nos permite analizar y caracterizar los conocimientos matemáticos de los menores trabajadores. Siguiendo a Chevallard, entendemos los tipos de tareas y las técnicas de la siguiente manera.

Alrededor de un tipo de tareas T, encontramos así, en principio, una tripleta formada por una técnica (al menos), t, una tecnología de ԏ, ѳ, y una teoría de ѳ, Ѳ. El todo en cuestión, denotado [T/ԏ/ѳ/Ѳ], constituye una praxeología puntual, que significa que se trata de una praxeología relativa a un único tipo de tareas, T (Chevallard, 1999, p. 228 [traducción propia]).

En particular, en esta investigación nos centramos en el estudio del saber-hacer en la proporcionalidad, que está constituido por la pareja (tipos de tareas, técnica). Estas herramientas teóricas de la tad nos permiten poner en relieve aquellos conocimientos que los menores movilizan en sus actividades laborales y que nosotros identificamos como conocimientos matemáticos relacionados con la proporcionalidad.

Es importante señalar que en nuestro estudio no hacemos uso exhaustivo de todos los elementos que conforman estas aproximaciones teóricas. Elegimos herramientas que nos permiten reconocer, analizar y resaltar el “carácter relativo” de los conocimientos matemáticos involucrados, los cuales se definen y adquieren utilidad dependiendo de la situación específica en que se movilizan (Brousseau, 2000). En nuestro caso, elegimos aquellas herramientas teóricas que nos permiten enfocar la mirada en las situaciones y los contextos específicos que enfrentan los menores trabajadores.

Si bien sabemos que el enfoque ecológico podría ofrecer herramientas de análisis desde la tad haciendo uso de la noción de institución (Castela, 2019), para nuestro estudio elegimos referirnos a relaciones sociales, restricciones y recursos de estructuración provenientes del contexto y que conforman las prácticas laborales de los pepenadores (Lave, 1991, 2011). Esto nos permite enfocar las historias de vida de los menores con quienes trabajamos, vinculándolas a las características de los contextos particulares en que estos niños laboran y que dan forma a sus conocimientos matemáticos.

A partir de estas elecciones teóricas, diseñamos una metodología para organizar el trabajo de campo que presentamos a continuación.

Metodología

Para el levantamiento de datos consideramos tres etapas: un acercamiento a los menores y su actividad laboral, a partir del cual pudimos elegir a nuestros informantes principales; acompañamiento en las actividades que realizan los menores elegidos para el estudio, y entrevistas para profundizar en las características de las tareas y las técnicas.

Para el acercamiento y el acompañamiento en las actividades laborales, el uso combinado de herramientas etnográficas y de la tad nos permitió identificar algunas tareas matemáticas que enfrentan los menores en sus actividades, específicamente aquellas que involucran relaciones de proporcionalidad. En la tercera etapa, una vez analizadas las tareas matemáticas que enfrentan los menores, diseñamos y realizamos entrevistas sobre la solución de tareas que involucran relaciones de proporcionalidad.

A continuación, presentamos las maneras en que diseñamos y llevamos a cabo cada una de estas etapas.

El acercamiento a las actividades laborales: los menores de este estudio y sus lugares de trabajo

Los menores fueron contactados en sus lugares de trabajo: mercados de la Zona Metropolitana del Valle de México; calles y depósitos de basura de las colonias Pensil y Polanco, de la delegación Miguel Hidalgo, el depósito de residuos sólidos Bordo de Poniente, en Chimalhuacán, Estado de México; y la terminal de transporte colectivo de la estación del metro Pantitlán, en la delegación Venustiano Carranza. La mayor parte de las veces, recurrimos a alguna persona conocida que nos introdujera con los niños, pero en ocasiones el contacto se dio de manera directa. Hicimos preguntas exploratorias destinadas a identificar las actividades laborales en que los niños participaban, poniendo especial énfasis en las características de su lugar de trabajo, sus relaciones familiares y su escolaridad. Incluimos algunas preguntas para saber si su actividad laboral involucraba tareas matemáticas relacionadas específicamente con la proporcionalidad.

Encontramos una enorme diversidad de actividades laborales que los niños realizan, tales como bolear zapatos en las calles y parques, lavar y cuidar coches, limpiar parabrisas o trabajar como “payasitos” en cruceros y avenidas, cargar bolsas de mercancía en mercados; vender chicles, mazapanes y otras baratijas al pie de los semáforos, en los camellones, en los vagones del metro, o fuera de algún cine; atender puestos de dulces, aguas frescas o recauderías;³⁵ vender cerillos y ajos en los tianguis; recolectar o, como ellos dicen, pepenar³⁶ productos reciclables en los basureros para después venderlos; cobrar el pasaje en los chimecos³⁷ o microbuses; trabajar como chalanes de albañil; vender agua en pipas… una infinidad de actividades en las que los menores buscan formas de obtener dinero para subsistir.

A través de estos primeros acercamientos, contactamos a un total de 20 menores, de entre 8 y 15 años de edad, de zonas pobres y marginadas de la Zona Metropolitana de la Ciudad de México. En el momento del estudio, 18 de ellos asistían a la escuela, ya sea la primaria, la secundaria o, incluso, alguna carrera técnica. Todos ellos fueron localizados en sus lugares de trabajo. Elegimos a dos menores trabajadores para realizar una observación detallada de su actividad laboral y entrevistas: Donovan, de 13 años, que se desempeñaba como chalán de albañil y ayudante en la venta de agua en una pipa en Chimalhuacán; e Isabel, de 10 años, pepenadora en la colonia Pensil. Estos dos menores se convirtieron en los informantes principales de nuestro estudio. Elegimos llevar a cabo el estudio con estos niños teniendo en cuenta, para comenzar, que participaran en una actividad laboral como su modo cotidiano de subsistencia; además, requerimos tener acceso a los lugares y los momentos en que realizan sus actividades laborales para poder observar in situ las tareas que realizan; y, finalmente, buscamos que sus actividades laborales cotidianas involucraran variadas tareas de proporcionalidad.

Las tareas matemáticas realizadas en las actividades laborales: el acompañamiento

Para los casos elegidos, llevamos a cabo un acompañamiento en la realización de las actividades laborales, destinado a observar en detalle las tareas matemáticas específicas de las cuales son responsables los menores, las técnicas que usan para resolverlas, sus interacciones con otros participantes de la actividad laboral (clientes, jefes o compañeros de trabajo), las herramientas que usan, y los lugares y las horas del día en que las realizan. Acompañamos a los menores a lo largo de seis meses (tres meses en la actividad de la pepena de cartón con Isabel y tres meses en la venta de agua con Donovan), en jornadas de entre cinco y ocho horas semanales, una vez por semana.

Al inicio del acompañamiento, el registro de los datos se hizo en un diario de campo al que agregamos algunos registros elaborados por los menores. Cuando evaluamos haber construido una relación de confianza suficientemente sólida con los menores y las personas participantes de la actividad, pedimos permiso para grabar algunos audios y videos.

A partir de este acompañamiento identificamos tareas de proporcionalidad que Isabel enfrenta en su trabajo. En la tabla 2 se muestran algunas de ellas junto con su estructura matemática.

Table 2. Ejemplos de las tareas observadas durante el acompañamiento de la actividad laboral de Isabel

Tarea observada (TO)	Estructura de la tarea
TO_A. Pagan $1.00 por kilogramo de cartón, si se venden en el depósito 15 kilogramos, calcular la cantidad del dinero que pagarán.	Peso del cartón	Lo que pagan en el depósito
	1 kg	$1.00
	15 kg	¿?
TO_B. Suponiendo que hoy sólo se recolectan 10 kilogramos de cartón, y pagan $1.50 por kilogramo, calcular la cantidad del dinero que pagarán.	Peso del cartón	Lo que pagan en el depósito
	1 kg	$1.50
	10 kg	¿?
TO_C. Si el precio pagado por kilogramo de cartón es de $1.20 y el total de cartón recolectado asciende a 69 kg, calcular cuánto pagarán por el total de cartón.	Peso del cartón	Lo que pagan en el depósito
	1 kg	$1.20
	69 kg	¿?
TO_D. Y si se recolectaran 20 kilogramos de periódico y pagan a 80 centavos cada uno, calcular la paga que darán en el depósito.	Peso del periódico	Lo que pagan en el depósito
	1 kg	80 ¢
	20 kg	¿?

En este capítulo nos enfocaremos en los resultados de la observación de la actividad y la entrevista realizada con Isabel. La observación de la actividad laboral de Isabel (etapas 1 y 2) se llevó a cabo durante los meses de febrero a mayo de 2011. En cada ocasión, Isabel y su familia (su mamá: doña Manuela, y Pancho, el hermano menor de Isabel que al momento del estudio tenía tres años) comenzaban la pepena desde temprano en la mañana, alrededor de las 8:00 a.m., y se prolongaba hasta por ocho horas. En el momento del estudio Isabel tenía diez años recién cumplidos. Desde antes de aprender a caminar Isabel ya acompañaba en la pepena a doña Manuela, su mamá, quien en un carrito de madera (en lugar del “diablo”, que actualmente usa) recolectaba el cartón. “Ahí trepaba a mi changuita”, nos dice la señora Manuela.

La entrevista: profundizando en los conocimientos de los menores

Las entrevistas se construyeron con el objetivo de profundizar en los tipos de tareas y las técnicas (Chevallard, 1999) que identificamos durante el acompañamiento, pero no pudieron ser discutidas con más detalle debido, entre otras cosas, a la premura con que se realizan las actividades y a la imposibilidad de interrumpir las interacciones constantes de los menores con otros participantes. Diseñamos tareas experimentales en las que modificamos algunas de las características (como el tamaño y la naturaleza de los números y cantidades involucradas, o las cantidades buscadas, entre otras) de las tareas observadas en la actividad laboral. A través de las tareas experimentales buscamos llevar al límite las técnicas que observamos en el acompañamiento, observar el uso de posibles técnicas alternativas, y dar espacio a reflexiones sobre los límites de su aplicabilidad.

Estas entrevistas con Isabel las realizamos en dos sesiones de tres horas cada una, en un salón acondicionado específicamente para esto ubicado en la Universidad Pedagógica Nacional-Ajusco, al sur de la Ciudad de México. Diseñamos 7 tareas experimentales, correspondientes a tareas de tipo proporcionalidad de valor faltante, comparación de razones y funciones afines (Block et al., 2010). La tabla 3 muestra una de las tarea que presentamos a Isabel durante la entrevista.³⁸

Table 3. Ejemplo de las tareas experimentales presentadas a Isabel durante la entrevista

Tarea experimental (TE)	Estructura de la tarea
TE_A. En un depósito pagan a $1.30 el kilo de periódico, ¿cuánto pagarían por 100 kilogramos?	Peso del cartón	Lo que pagan en el depósito
	1 kg	$ 1.30
	100 kg	¿?

Para cada una de las tareas experimentales y previamente a la realización de la entrevista, hicimos un análisis de su estructura matemática y sus posibles formas de solución. Por ejemplo, la tarea experimental A es del tipo problema típico de valor faltante (Block et al., 2010), que se puede resolver mediante una multiplicación. En esta tarea uno de los valores unitarios está dado: $1.30 por kilogramo de cartón. Involucra números naturales y decimales; y el factor interno que permite resolver el problema es: ×100, como se muestra en la tabla 4.

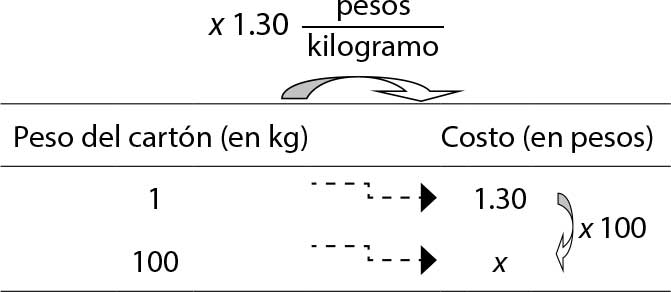
Para este capítulo, elegimos presentar el análisis de la tarea experimental A (te_a) para contrastar el procedimiento de solución que lleva a cabo Isabel con la solución que observamos en el acompañamiento a la tarea observada B (to_b). Aunque suponíamos que volvería a descomponer las cantidades, queríamos saber si cuando la cantidad después del entero es distinta de .50 (50 centavos), Isabel seguía aplicando las mismas técnicas.

Resultados del análisis y discusión

A continuación, presentamos los resultados del análisis de las observaciones correspondientes al acompañamiento y la entrevista de Isabel. Nos referiremos primero a las observaciones realizadas durante un día de acompañamiento a Isabel en la pepena de cartón; después, a una parte de la entrevista en la cual la solución de la tarea experimental presentada se puede contrastar con las soluciones de las tareas observadas durante el día de acompañamiento.

Pequeñas manos que trabajan en la pepena: entre cartones, calles y cuentas

Uno de los días de acompañamiento en la recolección de cartón parece que lloverá. Se da entonces una conversación entre la observadora (la primera autora de este capítulo) e Isabel. Como lloverá, es probable que sea un día malo para la pepena, pero Isabel dice: “Con esto no se sabe, a veces también nos va bien los días de lluvia”.

Debido a la premura de las acciones por realizarse para la recolección de cartón, no fue posible continuar este diálogo. Basándonos en este intercambio entre Isabel y la observadora, en observaciones anteriores y en los resultados de investigaciones previas, presentamos a continuación el análisis del procedimiento de Isabel centrándonos en las dos técnicas que empleó, una para encontrar la solución y la otra para verificarla.

Como se muestra en la tabla 5, en la tarea observada en el acompañamiento to_b hay cuatro cantidades puestas en relación: 1 kg de cartón, $ 1.50 (el precio correspondiente a 1 kg de cartón), 10 kg (la cantidad estimada de kilogramos recolectados) y la cantidad de dinero correspondiente a los 10 kg (la cantidad buscada o incógnita). Por su estructura, podemos decir que se trata de una tarea de multiplicación (Block et al., 2010).

En la tabla, las flechas destacan dos propiedades de la relación de proporcionalidad implicada en esta tarea: el factor externo constante que corresponde a multiplicar por $ 1.50 pesos cada kilogramo de cartón, y los factores internos que transforman las cantidades de ambos conjuntos haciéndolas 10 veces más grandes, es decir, multiplicando por 10.

Isabel resuelve esta tarea recurriendo a lo que llamamos propiedad aditiva de las relaciones de proporcionalidad (Block et al., 2010). Cuenta oralmente los kilos de cartón, uno por uno. A la par, va calculando cuánto le van a pagar por los kilos de cartón contados. La tabla 6 muestra esta forma de hacer el cálculo.

En las soluciones de las demás tareas identificadas durante el acompañamiento, observamos que Isabel recurre frecuentemente a la propiedad aditiva de las relaciones de proporcionalidad y tiene bien identificadas las situaciones donde es adecuado aplicarla.

Como ha sido reportado en otros estudios (véase, por ejemplo, Lave, 1991, 2011), también es común que Isabel verifique su resultado mediante la aplicación de otra técnica. En este caso Isabel decidió calcular 10 veces $1.50 a partir de la descomposición de cantidades, considerando por un lado la “parte entera” (10 veces $ 1) y por otro lado la “parte decimal” (10 veces 50 ¢). Isabel dice “primero los de ‘a peso’, serían… diez pesos, y luego los ‘cincuentas’ [lo que corresponde a las monedas de cincuenta centavos].”

En el acompañamiento no obtuvimos una explicación detallada de cómo procedió Isabel para calcular los resultados separados obtenidos de la descomposición de cantidades. Una posible técnica para encontrar los resultados es el uso de soluciones memorizadas que aparece muy comúnmente en la práctica, como es reportado por ejemplo por Lave (1991, 2011). En este caso la solución memorizada sería: 10 veces $1 son $10 (o diez monedas de un peso hacen diez pesos). Con los centavos pudo recurrir a otra solución común y memorizada en la práctica: 10 monedas de 50¢ forman $5. Esta solución proviene de las características específicas del sistema monetario mexicano (un recurso de estructuración, en términos de Lave, 2011), con el cual Isabel tiene mucho contacto debido a su actividad laboral.

Otra posibilidad es que Isabel haya procedido por agrupamiento repetido: agrupando pares de monedas de 50¢ para formar $1, lo cual también es una práctica usual de las actividades relacionadas con el manejo del dinero, debido a las características del sistema monetario mexicano. De hecho, cuando la entrevistadora le pide explicación, Isabel señala “pues de 2 monedas de cincuenta es un peso, ¿no?” Esta posible técnica se muestra en la tabla 7.

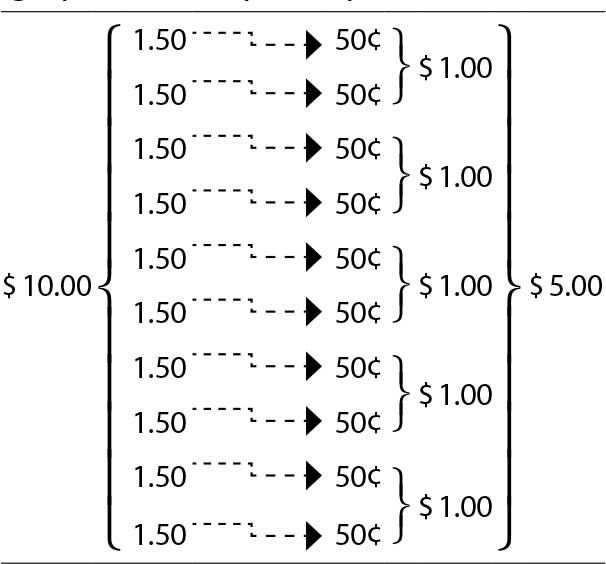
Sin embargo, debido a las condiciones de premura de la recolección, la gran cantidad de cosas que hacer (buscar, acomodar y atar el cartón en pacas, empujar el diablo, cuidar a su hermano, etcétera), entre otras, el cálculo de Isabel se dio tan rápidamente que consideramos muy probable que en este cálculo haya usado soluciones memorizadas.

El depósito: un lugar y un momento cruciales para la pepena

Al concluir la jornada de recolección, después de horas de caminar por las calles de la Ciudad de México, se lleva a cabo uno de los momentos climáticos de la actividad de la pepena: la venta de lo recolectado. Esta venta se da en depósitos de basura establecidos en la ciudad; doña Manuela e Isabel suelen ir a uno cercano a su casa. El encargado y dueño del depósito, llamado acopiador, recibe y determina el peso y el costo del material recolectado. Día con día, los precios por kilo de los materiales³⁹ se actualizan y se presentan en un cartel que se pone en la entrada del depósito.

Cuando Isabel y su familia llegan al depósito, se escucha un gran bullicio. Se oyen: el motor del camión de basura, el sonido del tren que pasa junto a este lugar, silbidos, música, ladridos de perros (que acompañan a algunos de los pepenadores). Hay otros pepenadores que están ya vendiendo su material. Por ahora, Isabel no entra al depósito, se sienta en la banqueta mientras doña Manuela le ordena: “¡Isabel, ahí cuidas a Pancho!”.

Doña Manuela empuja el diablo con el cartón hasta llevarlo cerca de la báscula y el montacargas. Isabel se sienta en la banqueta y juguetea con un perro. Después se dirige al lado de su mamá, el perro va con ella y la observadora los sigue. Entonces, Isabel se da cuenta de que ese día el precio del cartón es $1.20 por kilogramo y no $1.50 como había previsto en la mañana.

En el depósito están el acopiador y sus ayudantes, que son un “apuntador” que escribe en una libreta las cantidades de material que el acopiador pesa en la báscula y ayuda a sacar la cuenta de lo que se debe pagar; y otros trabajadores que ayudan a cargar y a separar el material de la pepena.

Isabel alcanza a doña Manuela en la fila de la venta, aunque le ha dicho que no entre al depósito.⁴⁰ Cuando llega el momento de la venta del material, Isabel ya está con su madre, cerca de la báscula para pesar el material recolectado. Ambas están alertas de las acciones del acopiador y del peso que marca la báscula.

En este día, la familia de Isabel logró pepenar en total 9 kg de revoltura, 35 kg de papel blanco y 69 kg de cartón.

Mientras le pagan a doña Manuela, Isabel va a la entrada del depósito a verificar que la tabla coincida con los precios que les han ofrecido por sus materiales. Entonces, por propia iniciativa y en voz alta, Isabel trata de calcular cuánto les pagarán por los 69 kilogramos de cartón recolectado. La observadora le pide que le explique cómo está haciendo sus cálculos.

Isabel: Uno veinte y uno veinte… dos cuarenta ¿no? Entonces… más otros dos… cuatro ochenta, más uno veinte… [Se ayuda con sus dedos, como una manera de controlar el número de veces que ha sumado $ 1.20. Sin embargo, pronto desiste de este procedimiento].

La tarea (to_c) que ahora intenta resolver Isabel es del mismo tipo que la que enfrentó por la mañana (to_b), al iniciar la pepena: se trata de encontrar la paga por cierta cantidad de cartón, conocida la cantidad de dinero que se paga por cada kilogramo (es decir, conocido el valor unitario). Sin embargo, las características de las cantidades involucradas son distintas: el tamaño de los números (por la mañana eran 10 kg, por la tarde 69 kg) y la parte decimal del precio por kilogramo (por la mañana: $ 1.50 por kilogramo, por la tarde: $ 1.20 por kilogramo).

Isabel intenta varias veces resolver esta nueva tarea (to_c) recurriendo a distintas técnicas. Hace dos intentos sumando el valor unitario ($ 1.20) consecutivamente (como lo hizo para resolver to_b), pero desiste. Luego, realiza una descomposición de los sumandos en pesos y centavos y explica a la observadora lo siguiente.

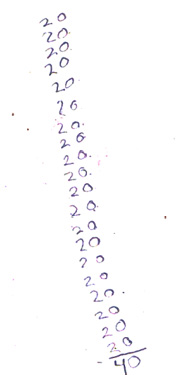
Para resolver esta suma, Isabel usa el algoritmo que usualmente se enseña en las escuelas de México: suma veinte veces 0 y coloca el número 0 debajo de la columna de las unidades; luego, suma 20 veces 2 mediante sumas iteradas de 2; y, verbalmente y con ayuda de su registro escrito, encuentra que 20 veces 2 es igual a 40. Pero escribe 4 debajo de la columna de las decenas, de modo que escribe 40 como resultado total de sumar 20 veces 20. Entonces ella misma pregunta: “¿son cuarenta?”, con duda y sin verificar su resultado. Mientras tanto, doña Manuela ya había recibido la paga.

A pesar de que ya son más de las cuatro de la tarde, doña Manuela le explica a la observadora “es que hoy fue todo muy rápido, no fuimos con tiempo”. Interrumpiendo, Isabel le pregunta a doña Manuela: “Oye, mamá, ¿y cuántos kilos fueron?”, pero doña Manuela tampoco contesta. “¡Ay, me duele mi espalda!”, dijo finalmente Isabel para sí.

En este momento de la pepena, logramos identificar varias maneras en que la realización de la actividad da forma a las técnicas usadas y, en consecuencia, a los conocimientos matemáticos involucrados. Se trata de una diversidad de aspectos no “matemáticos” de la actividad que tienen sentido para la realización de las tareas matemáticas en términos de la realización de la actividad laboral misma. Por una parte, encontramos que en el momento de la venta transcurren al mismo tiempo varias actividades casi de manera simultánea, que involucran interacciones con distintos participantes: el pesaje de los materiales recolectados, la verificación de los precios del día, la estimación de los montos por cobrarse, la verificación de las cantidades anotadas y de las cuentas, el cuidado de los niños, incluso tratar de llegar antes que algún camión de basura para no perder tiempo en el depósito, entre las que logramos identificar. El desarrollo de estas actividades obliga a doña Manuela y a Isabel a mantener su atención de modo diferenciado, priorizando entre otros aspectos el tiempo dedicado, como ya lo habíamos identificado desde las primeras observaciones. Además, la necesidad de recibir el pago correspondiente por parte del acopiador y sus ayudantes —y “que no las transen”, como dice Doña Manuela— las obliga a prever, estimar y verificar el peso de los materiales, los precios que se paga cada día y las cuentas que se realizan, aplicando a veces más de una técnica para realizar los mismos cálculos.

Las características del sistema monetario mexicano influyen también en las maneras en que Isabel resuelve las tareas. Como hemos mostrado, a pesar de tratarse del mismo tipo de tarea matemática (valor faltante que tiene asociada una multiplicación, de acuerdo con Block et al., 2010), las técnicas que aplica dependen de las características de los números y de la posibilidad de encontrar agrupaciones frecuentes en el sistema monetario, como la familiaridad en el manejo de “veintes” (monedas de 20 centavos de peso) o “cincuentas” (monedas de 50 centavos).

Finalmente, en nuestras observaciones encontramos que generalmente Isabel y su familia no usan recursos como el lápiz y papel en el desarrollo de su actividad laboral. A Isabel, el cálculo oral le permite cumplir con el cuidado a su hermano Pancho, al mismo tiempo que procura no perder de vista las acciones del acopiador y verificar las cuentas. La premura en la que se realiza la venta de cartón parece no permitir el cálculo escrito y, la interacción con el acopiador dificulta un cálculo exacto. La manipulación de cantidades lleva a un cálculo rápido y eficiente con resultados aproximados, que le ayuda a doña Manuela e Isabel saber en el momento que el acopiador está pagándoles “lo justo”.

La entrevista: llevando al límite las técnicas observadas en la actividad laboral

Como mostramos al presentar el episodio del acompañamiento de la actividad laboral de Isabel, muchas veces quedaron inconclusas discusiones sobre las técnicas aplicadas en la solución de las tareas. En general, la entrevista nos permitió profundizar y llevar al límite estas técnicas, así como dialogar con Isabel en torno a ellas.

A continuación, presentamos el proceso de solución que durante la entrevista Isabel dio a la tarea experimental A (te_a de la tabla 3). Esta tarea fue diseñada con la finalidad de contrastar y profundizar en los conocimientos observados para la solución de las tareas to_a, to_b y to_c, observadas durante el acompañamiento. Como hemos señalado, todas estas tareas son del mismo tipo (valor faltante que tiene asociada una multiplicación) pero involucran cantidades de distinta naturaleza y, en consecuencia, esperábamos que en la entrevista se movilizara alguna técnica alternativa. Sin embargo, la solución de Isabel fue completamente inesperada para nosotros: combinó conocimientos típicamente observados en la realización de su actividad laboral con conocimientos escolares, como a continuación mostramos.

Figura 2. Cantidades que Isabel multiplica para solucionar la tarea experimental TE_A

Isabel: Pues antes que todo creo que voy a hacer una multiplicación. [Escribe el algoritmo escolar de la multiplicación]. Cero por cero, cero; cero por cero, cero; cero por uno, cero. [Va diciendo oralmente cómo comienza la aplicación del algoritmo, para el primer renglón de la multiplicación. El resto del algoritmo sólo lo escribe. Cuando termina de multiplicar cada uno de los dígitos del multiplicador por el multiplicando pone puntos decimales en los productos parciales y obtiene 0.00, 3.00 y 1.00. Luego, suma y obtiene 13000, pero parece titubear al colocar el punto decimal; lo coloca dos cifras a la izquierda y obtiene 130.00. La figura 3 muestra la producción final de Isabel.]

Figura 3. Algoritmo de la multiplicación que Isabel escribe para solucionar la tarea experimental TE_A

Para obtener la solución de la tarea propuesta, Isabel recurre al algoritmo usual de la multiplicación, el cual no se había observado en la realización de la actividad ni se contempló en el diseño de la te_a. Además, basada en una estimación proveniente de su experiencia con el manejo del dinero, pudo controlar el resultado de aplicar el algoritmo y colocar correctamente el punto decimal. Ante la confrontación de la entrevistadora, quien le propone otra colocación del punto decimal (13.000), Isabel descompone el valor unitario en pesos y centavos ($1.30 = $1 + 30¢), y estima que por 100 kilogramos tendrían que pagarle más de $100. En contraste con las tareas observadas durante el acompañamiento (to_a, to_b y to_c), debido a las características del sistema monetario —y del sistema decimal de numeración—, las agrupaciones de lo que podríamos llamar “treintas” (monedas de 30 centavos) no están presentes como monedas y requieren combinaciones lineales para ser formadas con monedas del sistema mexicano (por ejemplo, 30 centavos son una moneda de 20 centavos y una moneda de 10 centavos; y 5 monedas de 30 centavos hacen $1.50, una moneda de un peso y una moneda de cincuenta centavos). Consideramos que éste es uno de los aspectos de la tarea te_a que promueven el uso del algoritmo por parte de Isabel.

Además, la posibilidad de resolver esta tarea durante la entrevista, en un espacio donde no están presentes las demandas de la actividad laboral, como la premura, las interacciones con los diversos actores, la posibilidad de ser estafadas y perder dinero, permiten a Isabel desplegar técnicas y conocimientos con los que cuenta pero que probablemente no son pertinentes en la realización de su actividad laboral. Cuando Isabel no usa el algoritmo, no se debe a que no disponga de técnicas matemáticas escolares “más refinadas” que las que usa en su actividad laboral, sino en buena medida a las demandas y restricciones que le impone la actividad de la pepena. Este resultado da cuenta también de procesos de circulación de conocimientos entre la escuela y la actividad laboral (Castela y Elguero, 2013; Castela, 2016), en los que bajo condiciones específicas —en la entrevista, en nuestro caso—, un conocimiento típicamente escolar como el algoritmo de la multiplicación puede ser usado para solucionar una tarea proveniente de la actividad laboral.

Conclusiones

Como mostramos en el análisis de datos, encontramos que la proporcionalidad aparece frecuentemente en las tareas que se resuelven en los contextos laborales de los menores trabajadores con los que se realizó este estudio. Específicamente con Isabel encontramos problemas típicos de valor faltante que involucran cantidades de distinta naturaleza. Estas tareas matemáticas identificadas en la actividad de la pepena son complejas debido al tipo de números involucrados (naturales y decimales) y al tamaño de las cantidades (desde centésimos hasta cientos, como en el caso del dinero); pero también por causa de las restricciones, condiciones y demandas bajo las cuales es realizada la pepena (como que el precio que se paga por kilogramo de cartón varía constantemente, o la tensión que tiene lugar en el momento en que el acopiador pesa el material, determina su precio y paga a los pepenadores). Además, las tareas que involucran relaciones de proporcionalidad y, en general, las tareas matemáticas no se encuentran aisladas en la actividad laboral, pues su realización depende de otras tareas tanto matemáticas como no matemáticas (por ejemplo, en el momento de la venta del cartón en el depósito, la tarea de venta está conformada por múltiples actividades y tareas en las que participan varios actores de la pepena, y de las cuales tienen que hacerse cargo doña Manuela e Isabel).⁴¹ Estas tareas se realizan para cumplir con un entramado denso de objetivos, formas de validación e interacciones provenientes de la actividad misma.

La actividad laboral, los conocimientos y las técnicas

Los menores trabajadores disponen de una diversidad de técnicas para enfrentar las tareas de proporcionalidad que les demanda su actividad laboral, pero en la realización de su actividad aparecen también conocimientos, tareas y técnicas que no son de naturaleza “puramente matemática” y que se conforman mutuamente con los matemáticos.

En el caso específico de Isabel, encontramos que ella pone en marcha técnicas basadas en el uso de razones internas y procedimientos sobre la marcha (Block et al., 2010), descomposición de cantidades y agrupamientos repetidos (Carraher et al., 1995), procedimientos híbridos y algoritmos adaptados sobre algoritmos escolares (Solares, 2012) y soluciones memorizadas (Lave, 2011). Además, realiza numerosas estimaciones sobre la cantidad de cartón recolectado y sobre la paga que se puede recibir en el depósito al momento de la venta.

En nuestras observaciones, encontramos que estas técnicas aparecen en distintos momentos de la realización de la actividad, dependiendo de aspectos que pueden determinar el uso de una técnica o de otra. Como mostramos en el análisis de resultados, uno de estos aspectos es la interacción de Isabel con otros participantes de la actividad: ya sean los miembros de su familia (doña Manuela y Pancho), el acopiador y sus ayudantes, u otros pepenadores. Estas interacciones son exigidas por la realización de la actividad y determinan, por ejemplo, si es momento de estimar un resultado, de verificarlo (mediante el uso de dos técnicas de cálculo), o si hay que calcular de manera exacta; o si hay que hacer las cuentas de manera oral o es posible escribirlas. Las interacciones de Isabel con su madre son muy variadas, van desde explicaciones que hace doña Manuela sobre cómo acomodar el cartón en el diablo, cómo hacer los nudos para atar el cartón, cómo vigilar el pesado que el acopiador hace del cartón recolectado o, incluso, sugerir operaciones específicas —como una multiplicación— para determinar la paga de cierta cantidad de cartón recolectado.

Es interesante señalar que, a diferencia de otros estudios (véase, por ejemplo, Solares, 2012), no se observó un uso frecuente de herramientas de cálculo (como calculadoras) ni de registros escritos (lápiz y papel). Esta ausencia se explica en términos de los rasgos que caracterizan a las actividades laborales observadas, que, por una parte, exigen priorizar las interacciones y la realización de otras actividades mientras se realizan los cálculos, lo cual dificulta enormemente el hacer cuentas por escrito o llevar una calculadora y usarla en medio de la realización de la actividad. Pero esto no significa que en otros momentos de la realización de las actividades laborales no aparezcan registros escritos o se usen herramientas de cálculo. Por ejemplo, en la pepena de cartón están los carteles que se colocan en las entradas de los depósitos mostrando el precio del kilogramo al que se compra cada tipo de material (cartón, papel, vidrio, pet, fierro, etc.). Además, por lo descrito por Isabel y doña Manuela, los responsables del depósito sí llevan registros escritos, pero no los muestran a los pepenadores. Queda pendiente averiguar cómo se producen esos registros, qué uso se les da y cómo interactúan en torno a ellos los participantes de la actividad.

Otro de los aspectos de la realización de la actividad que determinan el uso de ciertas técnicas corresponde a las características del sistema monetario. La variación de los precios del kilogramo de los materiales recolectados es cotidiana y los pepenadores deben ajustar constantemente las estimaciones del dinero que obtendrán por la pepena de cada día. Estas variaciones en el precio derivan en que Isabel use técnicas de agrupamientos repetidos, descomposición de cantidades, soluciones memorizadas o algoritmos híbridos que recuperan algoritmos escolares, dependiendo de las características de las cantidades involucradas y del sistema monetario. Es de estas maneras que las condiciones del contexto promueven el uso de una técnica u otra, dando así forma a los conocimientos matemáticos que se movilizan para la realización de las tareas que aparecen en la actividad laboral.

Implicaciones para la educación

Si bien en este estudio no se aborda el diseño de situaciones didácticas que integren a las clases de matemáticas los conocimientos que los menores trabajadores movilizan en sus actividades laborales, los hallazgos presentados sí nos llevan a preguntarnos: ¿qué sentido tiene recuperar para la escuela las situaciones problemáticas de los contextos laborales que involucran conocimientos matemáticos específicos?, ¿cómo llevar estos conocimientos a los salones de clases?

A partir de los resultados de nuestro estudio podemos identificar algunas características de las tareas de proporcionalidad de la actividad laboral de Isabel que podrían constituir “variables didácticas” para el diseño de tareas escolares (Brousseau, 2000; Block et al., 2010; Chaachoua y Bessot, 2019), a saber:

1. Los conjuntos de cantidades que se relacionan corresponden a magnitudes de diferente naturaleza: en todas las tareas observadas, las magnitudes son el peso del material, en kilogramos, y la cantidad de dinero que se obtiene por la venta del material, en pesos.
2. Generalmente, el valor unitario por kilogramo de cartón está dado, y puede ser un número natural o decimal (en consecuencia, el factor constante de proporcionalidad también es un número natural o decimal).
3. El valor unitario por kilogramo de cartón está en un rango entre 40 centavos hasta $1.50, poniendo en juego decimales hasta centésimos; para otro tipo de material, el valor unitario puede ir desde $1.50 hasta $15.

La variación de estas características puede promover la emergencia de técnicas que sean del interés del trabajo escolar. Así que podemos preguntarnos: ¿cuáles de estas variables pueden ser modificadas en el salón de clases de tal modo que se promueva el estudio y el desarrollo de la proporcionalidad?

Además de la riqueza y variedad de conocimientos matemáticos, consideramos que los resultados de este estudio aportan para que los menores trabajadores se hagan visibles a los ojos de quienes les enseñamos, porque ¿qué futuro le espera hoy a una niña como Isabel cuando la escuela difícilmente la retendrá en su educación básica?, ¿qué herramientas le puede ofrecer la educación —y la educación matemática específicamente— para enfrentar los retos y dificultades de su vida y de su trabajo?

Doña Manuela nos comenta que para ella es importante que Isabel vaya a la escuela porque la escuela ayuda para el trabajo. “Porque [haber ido a la escuela], pues sí, me ayuda para más o menos guiarme en las cuentas. Para no… para no destantearme tanto”, dice doña Manuela. Ella espera que la escuela le enseñe a Isabel a “valerse por sí misma. Si se llega a casar —que según ella no se va a casar nunca—, que no dependa. Sino que tenga estudios para que sepa ella que tiene algo con que defenderse”. Por nuestra parte, deseamos que este estudio contribuya a construir caminos y propuestas didácticas para responder a las esperanzas de doña Manuela e Isabel, y que seguramente comparten muchos menores que a la vez trabajan estudian.

Agradecimientos

A los niños trabajadores de este estudio que con sus realidades infantiles nos hicieron volver la mirada hacia ellos: Isabel, Gonzalo, Donovan, Jazmín, Irma, Jair, Luis Armando, Luis Ángel, Omar, Britany, Jaime, José Luis, David, Uriel, Adolfo, Cristian, Celestino, Cristiancito, Ángel y Moi, quienes desde los más variados rincones de la Ciudad de México (calles, estaciones de metro, autobuses, mercados, tiendas, polvorines) trabajan en la pepena, la albañilería, la venta de las más diversas mercancías, en la limpia y venta de pescado, cargando mercancías, barriendo calles, como meseros, fabricando fuegos artificiales, cobrando el pasaje de autobuses. Gracias por el regalo de sus historias, de sus conocimientos matemáticos, pero sobre todo porque con un guiño y de golpe nos hacen recordar que están en las aulas de las escuelas.

---

Bibliografía