11. La comprensión de los principios de agrupamiento y posición del sistema decimal de numeración en primero y segundo grados de primaria, ¿es posible?, ¿es necesaria?: Una reflexión crítica*

David Block Sevilla**

DOI: https://doi.org/10.52501/cc.132.11

Entrevistador: ¿Y si yo pusiera así? (dibuja en una tabla de decenas y unidades, lo siguiente)

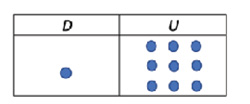
Alumno: Tengo 1. ¿Aquí hay 9?

E: Sí.

A: Tengo 1, me regalaron 9.

E: ¿Te da cuánto?

A: … 10.

E: ¿Por qué 10?

A: 1 + 9 me da 10.

[Lerner, 1992a: 172, 173.]

Resumen

Desde hace alrededor de 30 años se han multiplicado los resultados de investigaciones de corte didáctico y psicológico que demuestran que el aprendizaje de los principios de base y posición que subyacen al sistema decimal de numeración, son excesivamente complejos para los alumnos de los dos primeros grados de la primaria. Consecuentemente con ello, se han producido alternativas didácticas para el estudio del sistema decimal de numeración con un enfoque constructivista, con base en tales investigaciones. En México, la difusión y el estudio empírico de dichas alternativas es aún escaso y, en consecuencia, nuestros programas escolares se han modificado muy poco en este aspecto, en particular continúa la inclusión del contenido de valor posicional desde primer grado. En este texto desarrollo una reflexión sobre esta problemática. Constituye un ensayo dirigido a investigadores del área, a formadores de maestros, a diseñadores de programas de enseñanza de las matemáticas y a maestros preocupados por las dificultades mencionadas.

Palabras clave: sistema decimal de numeración, acercamiento constructivista, cálculo reflexivo, enseñanza, escuela primaria.

Introducción

En los años setenta del siglo pasado, la reforma curricular que se llevó a cabo en México para la enseñanza de las matemáticas estuvo animada por el espíritu de las “matemáticas modernas” que caracterizó a las reformas que se realizaron en varias partes del mundo en esa época. Una de las aspiraciones de ese espíritu renovador era enseñar unas matemáticas que requirieran del razonamiento y no de la memorización (Block y Álvarez, 1999). Se esperaba que los alumnos no solamente pudieran usar las herramientas matemáticas, sino que conocieran su fundamento. Un conocimiento en el que los cambios fueron notorios fue en el de la numeración en primer grado. Lo que antes se enseñaba con apoyo de billetes y monedas, al recitar y escribir series numéricas, dio paso a una enseñanza explícita de los fundamentos del sistema decimal de numeración (sdn). Antes de escribir el número 10, los alumnos debían comprender la noción de base (los agrupamientos recursivos: cada 10 unidades forman una decena, cada 10 decenas, forman una centena, etc.), y la noción de posición (cada una de las unidades compuestas —la decena, la centena, el millar, etc.— se representa mediante la posición de las cifras en el numeral). Este sistema es muy eficiente, permite generar números, compararlos y operar con ellos con máxima economía. Como muchos buenos inventos, permite hacer todo esto sin necesidad de comprender las entretelas del mecanismo. Pero, como comenté, un propósito de la enseñanza de las matemáticas que se enfatiza desde entonces es que los alumnos comprendan lo que subyace al funcionamiento de las herramientas. Un pedagogo de las matemáticas muy influyente en los años sesenta y setenta, Z. P. Dienes (1971), argumentó la conveniencia de que los alumnos estudiaran incluso numeraciones en bases no decimales atendiendo al principio de la “variabilidad conceptual” de su teoría sobre el aprendizaje de las matemáticas.²⁴ La meta era que los niños abstrajeran lo común a las distintas bases, y de esa manera accedieran a la estructura subyacente del sdn.

A lo largo de los últimos 30 años, sin embargo, tanto desde la docencia como desde la investigación se han multiplicado los indicios de que la manera en que se pretendió que los alumnos pequeños comprendieran el sdn y lo aprendieran a usar es prematura. Los docentes tienen grandes dificultades para propiciar esta comprensión. La investigación, por su lado, ha demostrado que la comprensión de los principios de agrupamientos recursivos y de valor posicional es mucho más compleja de lo que se pensó, para los niños menores de ocho años (Lerner et al., 1994). Podría considerarse que la enseñanza de dichos principios, aunque sea difícil, es necesaria debido a que éstos están implicados tanto en la comprensión del funcionamiento del sdn como en la de los algoritmos de suma y resta. Sin embargo, existen alternativas para acceder tanto al conocimiento del sdn como al de las operaciones de suma y resta en los primeros grados de primaria, las cuales no requieren conocer previamente, de manera explícita, los principios de base y posición del sdn.

Intentaré explicar lo anterior con más detenimiento en el presente texto. Primero, presentaré dos ejemplos tomados de clases comunes, es decir, no experimentales, uno de primer grado de primaria y otro de segundo, en los que se aprecian algunas de las dificultades que enfrentan tanto los alumnos como los docentes con la enseñanza del sdn. Después me referiré a trabajos de investigación sobre el tema, que explican una parte de la complejidad conceptual implicada para los niños. También haré alusión a las críticas que se han hecho a los medios didácticos utilizados en los últimos 50 años. En una tercera y última parte daré un breve panorama de vías alternativas que hoy en día se proponen para la enseñanza de la numeración y de las operaciones de suma y resta y, en el comentario final, mencionaré algunas de las dificultades para llevar a las aulas estos acercamientos.

Un asomo a dos clases

En el siguiente ejemplo (Hernández, 2020), una maestra de primer grado —con experiencia de 17 años dando clases—, implementó algunas lecciones de los libros de texto (Secretaría de Educación Pública [sep], 2018a, 2018b) con su grupo escolar, a petición de la investigadora. Centraré la atención en actividades realizadas en dos sesiones de clase, en las cuales la maestra se propuso que los alumnos establecieran que el conteo en grupos de 10 es más eficiente que el conteo de 1 en 1. Cabe observar que la lección del libro no especifica que los conteos sean de 10 en 10, aunque probablemente esa intención subyace. La maestra procuró que los alumnos cuantificaran colecciones de alrededor de 50 elementos y, después, que expresaran el resultado mediante un número de grupos de 10 y de elementos no agrupados. Esta

descomposición de la cantidad se vincularía enseguida con el nombre del número. Veremos algunos de los esfuerzos reiterados e infructuosos de la docente por dar lugar al conteo de 10 en 10, siguiendo las indicaciones de una actividad del libro de texto (véase la figura 1).

En la primera sesión observada la maestra entregó a los alumnos, organizados en equipos, la cantidad de 52 cubos con la consigna siguiente:²⁵

Ma: Vamos a contar, a ver quién gana a contar cuántos cubitos tiene cada equipo.

Después de un primer ensayo fallido —cada alumno del equipo metía cubos a una caja y contaba los cubos que metía, pero no obtenían la cantidad total de cubos introducidos por todos— se repitió la instrucción, y los alumnos se dieron a la tarea de contar de uno en uno. Muy pronto, la maestra los interrumpió para intentar favorecer el conteo por grupos de 10.

Los niños, relata la autora del estudio (Hernández, 2020), realizaron sus torres (una base de 3 × 3 y un cubo encima). Sin embargo, agrega, “en lugar de contar de diez en diez, lo hicieron de uno en uno; es decir, contaban los cubos que formaba cada una de las torres” (p. 85). La docente lo intentó de nuevo.

Se puede advertir, comenta la autora, la intención de la profesora de impulsar el conteo de diez en diez, al decir pongan las manos atrás (Hernández, 2020, p. 86). Sin embargo, los niños siguieron contando de uno en uno, y al final, la docente los animó a seguir. Están en juego dos unidades de conteo (las unidades y las decenas), lo que hace la comunicación un poco confusa, y esto se agrava pues en un primer momento la maestra preguntó por el número de torres y, cuando le contestaron (dos), rechazó la respuesta y preguntó por el número de fichitas. Hubo todavía un intento más por parte de la profesora de que los niños contaran de 10 en 10, en el momento de la verificación. Los alumnos recitaron la serie de 10 en 10 —como esperaba la maestra—, pero lo hicieron independientemente de la idea de contar los objetos —tal y como se ha documentado que los niños pequeños proceden a veces, en sus primeros intentos de conteo de 1 en 1— (Brousseau, 2000).

En la segunda sesión, la maestra, insatisfecha con los resultados de la primera, decidió trabajar una actividad en la que los alumnos tendrían que agrupar colecciones iguales, en diferentes agrupamientos: 2, 3, 5, 7. Cabe señalar que en el libro del maestro se sugiere una actividad similar, con la expectativa de que los alumnos descubran que el agrupamiento de 10 en 10 es más sencillo (véase la figura 2).

Pero la idea de la docente iba más allá, ella explicó que esperaba que los niños vieran que el tamaño de los grupos que se forman no altera a la cantidad total. Intituló la actividad como “sentido conservación de la cantidad”, probablemente evocando la “invarianza de la cantidad” mencionada en el libro del maestro, en relación con una de las operaciones que subyacen a la construcción del número.²⁷ Sin embargo, no queda claro en qué ayudaría esta actividad a los alumnos para descubrir las ventajas del conteo de 10 en 10. La actividad fue difícil de llevar a cabo, pues aunque los alumnos hacían los grupos solicitados, a la hora de decir cuánto había en total, naturalmente contaban de uno en uno, y a veces cometían errores.

Veamos ahora una sesión de clase de un grupo de segundo grado, desarrollada por una maestra quien compartió su experiencia en un grupo de trabajo colaborativo a distancia, formado por algunos maestros y algunos investigadores, durante dos meses del periodo de confinamiento debido a la pandemia por covid 19 (Macías, en proceso). La maestra interactuó con sus alumnos a través de diferentes medios, mensajes de Whats, clases demostrativas por Facebook (fb), cápsulas de TikTok, etc. Tuvimos poco acceso a lo que hicieron los niños, excepto por breves momentos a través de algunos de los videos que la maestra compartió.

A continuación, me centraré en una clase que la maestra dio por Facebook, como antecedente para que sus alumnos resolvieran tres lecciones del libro de texto (sep, 2019). Tanto en la sesión como en el libro de texto, las actividades estuvieron dirigidas a expresar números de tres cifras, de dos maneras distintas: considerando los agrupamientos de unidades, decenas y centenas (lo que lleva a la escritura convencional), y sin usar centenas (lo que obligaría a considerar un número mayor de decenas). Lo que varía de una lección a la otra es el referente concreto: primero papas empacadas en cajas de 100, de 10 y papas sueltas; después, fichas de colores que representan los distintos agrupamientos; luego, tablas de centenas, decenas y unidades; le siguen billetes y monedas y, finalmente, escrituras aditivas, por ejemplo, 100 + 80 + 5, o bien 180 + 5. El valor de las fichas que se utilizaron ya estaba establecido: las azules valen 1, una roja 10 azules y una verde 10 rojas o 100 azules. A continuación presentamos una interacción entre la maestra y un alumno.

Más allá del cambio de número que la maestra hizo involuntariamente al principio, de 442 a 542, es manifiesta la dificultad de las relaciones que intenta comunicar. Responder a la pregunta “¿Cómo hacer 542 con las rojas?” implica, para los pequeños de segundo grado, tener presente que cada ficha roja vale 10; calcular cuántas veces cabe 10 en 542, ya sea sumando de 10 en 10, lo cual es un proceso largo, o de 100 en 100, si ya saben que en 100 hay 10 de 10; o, por último, inferir directamente de la escritura que en 542 hay 54 decenas, casi imposible que sepan esto, en todo caso es a lo que se aspiraría que aprendieran. Ante las dificultades de los niños, la maestra optó por dar la respuesta: “si lo piensas, tendrías que hacer 54 rojas”, y continuó con la obtención de las fichas verdes, que representan centenas: “pero puedes usar algunas verdes, ¿Por qué no conviertes tal vez dos verdes, dos verdes a rojas?” La sugerencia de convertir 2 verdes a rojas, tendría la finalidad de que los niños, al ver que 2 verdes corresponden a 20 rojas, pudieran inferir por ellos mismos que entonces, si se tienen 54 rojas, alcanza para más de 2 verdes, quizás lo doble, 4 o 5. Pero los niños no lograron seguir estos razonamientos. Un alumno mencionó “tengo 500 rojas para formarlos”. Probablemente quiso decir “500 azules para formar las rojas”, y en ese caso se encaminaba bien. Lo que la maestra buscaba es que los alumnos comprendieran que 542 se puede componer no solamente con 5 verdes, 4 rojas y 2 azules, sino también con 54 rojas y 2 azules, lo cual es difícil. Cabe destacar que tampoco es claro qué utilidad tiene, en segundo grado de primaria, dicho conocimiento. Ya de por sí es complejo que comprendan que en un número de tres cifras cada cifra corresponde a un agrupamiento distinto (100, 10 y 1).

Posteriormente, la maestra pidió a sus alumnos que resolvieran tres lecciones del libro de texto gratuito²⁸. En las tres lecciones, resulta complicado entender a qué se refiere la instrucción de formar un número “de distintas maneras”, sobre todo cuando solamente una de esas maneras corresponde al agrupamiento usual en el sistema decimal, y es, además, la más económica. La instrucción habría sido más clara si se hubiera planteado algún motivo que justificara la ausencia de centenas, por ejemplo, “si no hubiera cajas de 100, ¿cómo se podrían empacar la papas?”, o bien, “si no hubiera billetes de 100, ¿cómo se podría entregar la cantidad de dinero?”

A título de ejemplo, veremos una de las tres lecciones (véase la figura 4) y la ayuda que la maestra proporcionó.

La maestra, tal como lo señala el libro, da a los alumnos un número, elige el 643, y les pide que lo representen “de dos formas”. Para ello, la maestra envía por Facebook una ayuda suplementaria (véase la figura 5).

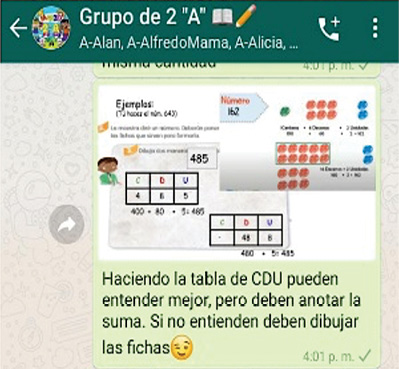
En la ayuda, se presentan dos formas de agrupar las cantidades de 485 y 162: una agrupando en centenas, decenas y unidades, y la otra agrupando solamente en decenas y unidades. Para el 485 se usa una tabla y para el 162, fichas de colores, iguales a las del libro de texto. En ambos casos, además, se incluye una tercera representación con sumas, por ejemplo, para 485 = 400 + 80 + 5 y 480 + 5.

En la ayuda que envió (figura 5), la maestra sugiere a los alumnos dibujar fichas de colores en caso de que se les dificulte trabajar con la tabla de centenas, decenas y unidades. Sin embargo, en su papel de representar agrupamientos, las fichas son casi tan abstractas como la tabla.

Las lecciones del libro de texto están diseñadas bajo el supuesto, muy incierto, de que el cambio de representación, de objetos “reales” (papas), a objetos en los que los agrupamientos están simbolizados con colores (fichas) y finalmente a números en tablas y a sumas, ayudará a comprender la noción en juego, a saber, que si bien cada cifra de un número indica un tipo de agrupamiento (en 185 hay 1 centena, 8 decenas y cinco unidades), hay otras lecturas posibles que se pueden hacer: hay 18 decenas y 5 unidades, o bien, hay 185 unidades. No es fácil que un alumno de segundo grado comprenda esta diversidad de formas de componer los agrupamientos, sobre todo porque, como ya comenté, ese hecho no cumple una función.

Después del trabajo con las tres lecciones, siguió el estudio del algoritmo de la suma, para el cual la maestra ofreció como apoyo otro pequeño video elaborado en la aplicación Tik Tok, en el que el algoritmo se ilustra con fichas de colores. En el video, la maestra plantea tres sumas sin contexto, en tablas de unidades, decenas y centenas. En la primera suma (4 + 1 + 6) el resultado, 11 unidades, aparece en la columna de las unidades, pero un renglón más abajo aparece un 1 en la columna de las decenas y otro en el de las unidades; de manera parecida, en la segunda suma (30 + 60 + 50), el resultado que aparece es 14 decenas, y en el renglón siguiente 1 centena y 4 decenas.

Las explicaciones, y las representaciones en la tabla, son muy claras para quien, como nosotros, ya sabe de lo que se trata. Pero ¿lo son para los alumnos de segundo grado?

Como dejan ver estas dos clases, los principios que subyacen al sdn, a saber: organizar la cantidad en grupos de 10 unidades, y en grupos de 10 grupos de 10 unidades, etc., de manera recursiva; concebir cada tipo de agrupamiento como una unidad compuesta, y representar la cantidad de cada una de esas unidades mediante la posición de la cifra en el número, resulta difícil de aprender, y también muy complicado de enseñar. Pero, además, hay otra cuestión problemática con el uso del material de las fichas de colores: si se usa el color, la posición de las cifras ya no juega un papel y, sin embargo, es algo que se pretende enseñar.

Dificultades conceptuales subyacentes a la comprensión del SDN

Lerner (1992a; et al., 1994), investigadora argentina, ha mostrado desde hace ya más de 20 años, mediante numerosos ejemplos, que los alumnos empiezan a comprender lo que significa el “llevo uno”, o “pido prestado” mucho después de los primeros grados de primaria, hasta alrededor de quinto grado. Transcribiré primero un ejemplo proporcionado por la autora en el que se pide a un alumno de primer grado —Rafael, quien ya había recibido alguna enseñanza sobre el valor posicional— explicar qué significa que un número tenga 2 decenas (pp. 167 y 168). Ella utiliza una representación de tablas de decenas y unidades.

Entrevistador	Rafael
¿Sabrías escribir esto en números?	(Escribe 8 en su hoja)
¿Por qué habrán dejado ese cuadro vacío?	Porque allí va un 0
Si yo en este sitio (lugar de las decenas) pongo 2 puntos, ¿qué significarán?, ¿cómo escribirías ahora?	8 más 2 (escribe). 8 + 2
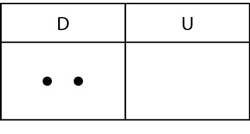
Ahora escribe esto en números:	¿Entre la unidad y la decena? (Escribe) 2 + 0
¿Qué será una decena?	Decena es de 10 elementos.
¿Cuántas decenas hay aquí?	2
¿Y cuántos elementos?	2
¿Dos elementos o decenas?	2 elementos.
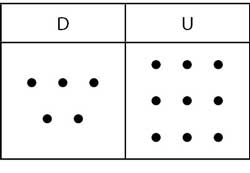
Ahora escríbeme esto en números	(Escribe.) 9 + 5

Rafael asigna a los puntos el carácter de unidades simples, independientemente de si están ubicados en la columna de las decenas o de las unidades. Cuando se plantea la actividad inversa, poner en una tabla los puntos que corresponden a un número escrito, para “8” él pone 8 puntos en la columna de las unidades y para “13” pone 13 puntos en la columna de las decenas y explica: “porque es una suma, cuando uno suma se empieza por las unidades y después por las decenas”. Éste es uno de numerosos ejemplos muy similares.

Más adelante en la misma obra, Lerner (1992a, pp. 189 y 190) presenta entrevistas a alumnos de tercer grado a quienes se plantearon sumas de cuatro cifras y se les interrogó sobre la razón por la que, cuando una suma parcial excede de 9, solamente ponen la cifra de las unidades, se dice “llevo 1”, y se agrega esa unidad de las cifras de las decenas. Ninguno de los alumnos entrevistados lo pudo explicar. Veamos un ejemplo.

Entrevistador	Rafael
1845 + 425 187 2457	[La hace bien. Mientras la resuelve, va diciendo:] “5 más 5… 10, y 7, diecisiete, llevo una… 5 y 2… 7 y 8… 15, llevo una […]”
Mira, mi amor: ahora yo te estoy oyendo que dices: 5 y 5…10 y 7… 17, ¿no?, llevo 1, entonces aquí el 4 en vez de 4 dices 5, y 2… 7…	(Me interrumpe.) Porque llevo una ¡y 4 son 5!
Ajá, pero ¿qué es ese 1?	…Este… el 1 de 7 [17] que no se lo puedo poner aquí [al lado].
¿Por qué no?	Porque… no sé.
Y entonces, ¿por qué será que lo pasas para arriba?	…
Ajá, ¿qué parte del 17 será ese 1?	… ¡El 1!
Pero dentro de esa cantidad, 17.	No sé.
¿Eso tendrá algún valor?	… ¿El 1?
Ajá	… No sé tampoco.
¿Y a ti no se te ha ocurrido pensar qué puede pasar si nosotros ponemos la cantidad completa?	No.
O sea, que en vez de dejar el 7 sólo y llevar el 1, entonces pongamos el 17 completo. ¿Se puede hacer?	… No sé… porque a mí no me han dicho qué significa este… yo no sé por qué uno tiene que poner el 1 aquí.

Comenta la autora (p. 192):

Si hubieran sido unos pocos niños los que nos hubieran dado este tipo de respuestas, podríamos pensar que se trata de una dificultad particular de esos niños. Pero ocurre que todos los niños de tercer grado que entrevistamos nos respondieron de este modo y ningún niño vinculó el significado de “llevarse uno” o de “pedir prestado” con el valor posicional.

¿A qué se deben estas dificultades de los alumnos de los primeros grados para comprender el significado de la cifra “1” que se pone en el lugar de decenas? El sistema de numeración tiene un fuerte componente multiplicativo. La formación de agrupamientos se hace de manera sistemática y recursiva: grupos de 10 elementos, grupos de grupos de 10, grupos de grupos de grupos de 10, etc., lo que da lugar a que el número de elementos de cada agrupamiento sea una potencia de 10: 10⁰, 10¹, 10², 10³, ... Cualquier cantidad se expresa como una combinación lineal de estos agrupamientos, por ejemplo,

5 × 10³ + 2 × 10² + 8 × 10¹ + 6 × 10⁰

Finalmente, el sdn incorpora el genial recurso de usar la posición de las cifras para indicar la potencia de la base que corresponde, con lo cual la escritura se simplifica enormemente. El número anterior se representa así: 5286. La naturaleza multiplicativa del sistema decimal de numeración explica por qué la comprensión de su mecanismo es compleja, y por lo tanto dista de lo que los pequeños de los primeros grados, quienes apenas están accediendo a operaciones aditivas, pueden comprender (Lerner, 1992a y Lerner et al., 1994).

Otros investigadores que han estudiado el proceso de construcción de la secuencia numérica por los niños pequeños (Steffe, 1994; Olive, 2001), señalan que la posibilidad de concebir y manejar estas unidades compuestas iterables —compuestas porque valen 10; iterables, porque se pueden repetir y contar—, corresponde a la construcción de lo que ellos llaman secuencia numérica general, con la cual culmina un proceso relativamente extenso que transcurre a lo largo de los primeros años de la primaria. Las unidades compuestas iterables, propias de la secuencia numérica general, son la base del pensamiento multiplicativo: comprender el significado de, por ejemplo, 3 veces 10, supone saber que 10 unidades forman una nueva unidad que se puede repetir y contar, es decir, es iterable.

Con respecto a los numerosos intentos que se han hecho por ayudar a los pequeños a comprender el principio de la posición de las cifras mediante representaciones “intermedias” como lo son las fichas de colores, o el uso de tablas de columnas, varios estudiosos del tema (Lerner, 1992b; Broitman et al., 2011; Quaranta et al., 2003, entre otros) consideran que no son pertinentes²⁹. Señalan que la presencia de objetos físicos o icónicos diferentes para representar a los agrupamientos hace innecesario el uso de la posición, que es justamente lo que se quería explicar; por otra parte, destacan que “se impide que los chicos utilicen los conocimientos que ya han construido en relación con el sistema de numeración” (Lerner, 1992b, p. 13). Las evidencias de que los alumnos suelen tener conocimientos sobre el sistema de numeración, aprendidos muchas veces fuera de la escuela, constituyen uno de los aportes más interesantes de sus indagaciones con los niños, así como de su propuesta didáctica. En el apartado 3 volveré sobre ello.

Así, actualmente está bien documentado el hecho de que el componente multiplicativo que subyace al sistema es complejo para los aprendices de los primeros grados de primaria. Debido a ello, desde hace ya más de 20 años se han empezado a explorar vías alternativas de entrada a la numeración decimal. En lo que sigue, presentaré una de estas alternativas, la cual asume una perspectiva constructivista sobre los procesos de aprendizaje de la numeración, en tanto sistema de representación. Cabe aclarar que no se plantea omitir la enseñanza de los principios que rigen al sdn: base y posición. Lo que se argumenta es la pertinencia de enseñarlos de otra manera, y, un poco después. Sobre todo, se argumenta no considerarlos como requisito previo para apropiarse de la numeración. Suele contraargumentarse que dichos principios son necesarios para que los niños aprendan a sumar y restar. Sin embargo, como veremos enseguida, existen formas alternativas de sumar y restar accesibles y formativas para los niños, fincadas en una postura constructivista sobre los procesos de aprendizaje de las matemáticas, que no consisten en operar con los valores absolutos de las cifras de los números, es decir, por ejemplo, en una suma como 29 + 35, no plantean sumar las cifras 9 + 5 y 2 + 3, sino los valores relativos de éstas, 20 + 30 = 50; 9 + 5 = 14 y finalmente 50 + 14 = 64, o bien, 29 + 1 = 30 y 30 + 34 = 64, y que por lo tanto no requieren comprender la noción de valor posicional.

Alternativas didácticas para la enseñanza de la numeración y de las operaciones de suma y resta, en los primeros grados

Aprendizaje de la numeración

¿Cómo aprendieron a usar los números las personas adultas que no tuvieron oportunidad de alfabetizarse en la escuela? Varias investigaciones han puesto en evidencia desde hace ya varias décadas, importante capacidad de cálculo mental de dichas personas (véase, por ejemplo, en México, Ávila, 2005; Ferreiro et al., 1987). A lo largo de su vida, los adultos logran conocer la numeración oral al identificar poco a poco sus regularidades, tales como la repetición de la serie del 0 al 9 en cada rango de las decenas (veintiuno, veintidós, veintitrés…. treinta y uno, treinta y dos, treinta y tres…); el orden en que se suceden las decenas, similar al de los dígitos (diez, veinte, treinta, cuarenta… noventa), lo mismo que las centenas; el cambio de decena después de un 9 (1920, 2930, etc.), entre otras. Las personas no escolarizadas llegan a dominar la numeración oral en cierto rango, y a ponerla al servicio de sus cálculos. Los niños aprenden la numeración oral de una manera parecida: al escucharla, al identificar regularidades, al usarla. Seguramente ésa es la razón por la cual la numeración oral no ha sido un objeto importante para la enseñanza escolar, a diferencia de la numeración escrita, la cual no se adquiere fácilmente sin una intervención didáctica.

Probablemente la numeración, sobre todo la oral pero también la escrita, es de los conocimientos de matemáticas con los que más interacción tienen los niños desde temprana edad fuera de la escuela.

Dado que la numeración escrita existe no sólo dentro de la escuela sino también fuera de ella, los niños tienen oportunidad de elaborar conocimientos acerca de este sistema de representación desde mucho antes de ingresar en primer grado. Producto cultural, objeto de uso social cotidiano, el sistema de numeración se ofrece a la indagación infantil desde las páginas de los libros, las listas de precios, los calendarios, las reglas, los talonarios de la panadería, las direcciones de las casas… (Lerner et al., 1994, p. 97).

Este hecho está detrás de una constatación relevante que se ha generado desde la investigación: los niños, desde preescolar, al interactuar con las numeraciones oral y escrita fuera de la escuela desarrollan hipótesis sobre sus características. Así, por ejemplo, a partir de cierto momento saben que cuantas más cifras tiene un número, más grande es o bien, que si dos números tienen la misma cantidad de cifras, es más grande el que tiene el número mayor a la izquierda (Lerner et al., 1994). Por supuesto, no todas las hipótesis que los niños elaboran son correctas, o completas, de manera que suelen entrar en contradicción. Estas contradicciones pueden ser, sin embargo, uno de los motores de la evolución de su conocimiento. Por ejemplo, la tendencia a escribir los números como se escuchan, puede llevar a un niño a escribir el 158 así “100508”. Pero si ese niño ya sabe también que doscientos se escribe “200” —en general los números que tienen un dígito seguido de ceros, llamados nudos, son los primeros de varias cifras que aprenden a escribir—, la hipótesis infantil de que entre más cifras tiene un número, más grande es, lo llevará a una contradicción: el doscientos es más grande que el ciento cincuenta y ocho (pues aparece después en la serie), pero “200” tiene menos cifras que “10058” y entonces, 158 es mayor. Poco a poco, mediante un trabajo docente oportuno que ayude a poner en evidencia las contradicciones —sin duda esto no es sencillo—, los alumnos reorganizan su conocimiento. Lerner et al. (1994) relatan, por ejemplo, el caso de Nadia, una niña de 6 años quien, después de vivir la contradicción que mencioné antes (en este caso se trató del número 2558), y a partir de otro conocimiento que ella tenía, a saber, que los números del orden de los miles llevan cuatro cifras, encontró por sí misma la solución: sobrescribió el 500, el 50 y el 8 sobre los ceros de la derecha de 2000, formando 2558 (Lerner et al., 1994: 130). Estas observaciones, fundamentales desde un marco constructivista del aprendizaje, han llevado a un principio para la enseñanza de la numeración: primero usarla, escribir números y compararlos y, a partir de las dificultades que surjan, de la reflexión sobre ellas, de las regularidades encontradas, de la confrontación con las producciones de otros, etc., conceptualizarla, esto es, descubrir los principios de agrupamiento recursivo y de representación posicional, y no al revés: primero pretender conceptualizarla para después usarla (Terigi y Wolman, 2007, pp. 72 y 73).

Es decir, los principios de base y posición que rigen el sdn podrían ser comprendidos progresivamente por los alumnos al reflexionar sobre sus propias escrituras, mediante una conducción docente adecuada. Los alumnos no necesitan saber que en el número 21 el 1 representa unidades y el 2 representa decenas para poder escribir ese número, para saber que es el siguiente de 20, que es menor que 25, mayor que 19, etc. En cambio, saber cosas como que 21 y 12 no son los mismos números, aunque se escriban con las mismas cifras, o descubrir que 21 no se puede escribir “201”, porque entonces sería más grande que 30, aunado a un trabajo docente que favorezca la emergencia de estos hallazgos, que ayude a destacar las contradicciones y propicie reflexiones, los podría ayudar a comprender, poco a poco, el valor posicional de las cifras de un número, esto es, volviendo al ejemplo, que el 1 representa una unidad y el 2 tanto 20 unidades como dos decenas.

¿Qué hacer entonces? Varios investigadores recomiendan enseñar a los alumnos las dos numeraciones, la oral y la escrita, y propiciar el análisis de las relaciones entre ambas, sus semejanzas, y sobre todo sus diferencias (cf. Mounier et al., 2020). Con respecto a la numeración escrita con cifras, avanzar en dos frentes: la identificación de regularidades de la serie y, poco a poco, recurrir a la agrupación de colecciones con base 10 y representar los agrupamientos.

Las colegas argentinas recomiendan, con base en sus investigaciones, aprovechar los conocimientos previos de los niños sobre ambas numeraciones para identificar regularidades, generar hipótesis y dar lugar a conflictos que, al resolverse, les permitan avanzar. En términos muy generales podría decirse: multiplicar las experiencias en el aula en las que cuantifican y se forman colecciones, se expresan oralmente números, se escriben y se ordenan, se comparan escrituras, se comparten hallazgos.

En las obras citadas de Broitman et al. (2011), Lerner (1992a) y Terigi y Wolman (2007), entre otras (véase también el interesante trabajo, dirigido a docentes, de Parra y Saiz, 2007), el lector encontrará numerosas sugerencias claras y fecundas.

Aprendizaje de los procedimientos para sumar y restar

De acuerdo con las investigaciones que hemos mencionado, la comprensión de los principios de base y posición requiere a su vez de una comprensión de aspectos multiplicativos implicados en dichos principios, y esto por lo general se logra hacia el tercer grado de primaria. Sin embargo, algoritmos de la suma y la resta que se enseñan actualmente en las escuelas descansan en los principios de base y posición: las cifras de cada orden (unidades, decenas, centenas, etc.) se suman o se restan entre sí. Para sumar, por ejemplo. 35 más 81, se suman el 3 y el 8, y no el 30 y el 80. Las 11 decenas que se obtienen dan lugar a una centena, etc.

Como vimos anteriormente, comprender las razones que explican estas características del algoritmo, por ejemplo, la razón por la cual se suma 3 y 8 y no 30 y 80, o la razón de “llevar uno”, son prácticamente inaccesibles para los pequeños de los primeros grados. Para ellos, estos algoritmos son susceptibles de memorizarse y reproducirse, pero no de comprenderse. Por lo anterior, puede ser conveniente posponer la enseñanza de los algoritmos que descansan en esas propiedades, hasta tercer grado. Durante los primeros dos años de la primaria sería recomendable trabajar con acercamientos alternativos al de los algoritmos usuales, más intuitivos. Esto es lo que veremos a continuación.

Al mismo tiempo que se ha desarrollado una vigorosa propuesta de la enseñanza de la numeración —oral y escrita— y de los principios del sdn, ha tomado forma un acercamiento alternativo —afín a dicha propuesta— para la enseñanza de las operaciones de suma y resta, frecuentemente bajo el nombre de cálculo mental reflexivo (Parra, 1994; Parra y Saiz, 2007; Gálvez, et. al., 2011; Askew, 2004; Butlen, 2007, Caballero 2018). De acuerdo con Parra (1994), el cálculo mental reflexivo es:

Así, los conocimientos sobre la numeración, y sobre procedimientos alternativos para sumar y restar se realimentan unos a otros: “Desde la perspectiva didáctica, focalizar en la relación existente entre notación numérica y operaciones aritméticas constituye un escenario privilegiado para profundizar la comprensión del sistema de numeración (Terigi y Wolman, 2007: 76)”.

A continuación, presento tres ejemplos de procedimientos para sumar desarrollados por alumnos de segundo grado, durante un proyecto experimental sobre prácticas de cálculo mental (Caballero, 2018, pp. 144 a 149).

Para la suma 23 + 18, un alumno suma por separado las decenas y las unidades de la siguiente manera:

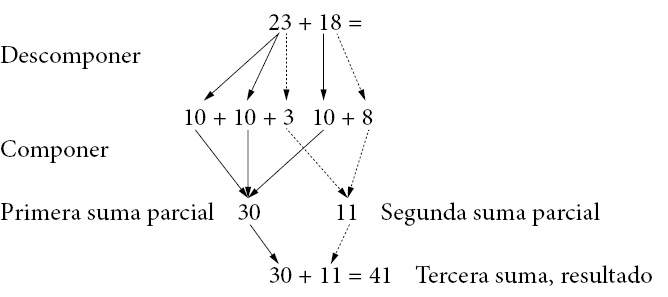
También es posible descomponer un solo sumando en decenas y unidades y tomar del otro sumando las unidades que hagan falta para completar otra decena, por ejemplo, un alumno realiza las siguientes descomposiciones para sumar:

35 + 8 =	15 + 9 =	18 + 22 =
35 + 5 + 3	15 + 5 + 4	18 + 2 + 20

Como se puede observar, estas formas de sumar no ponen en juego la noción de agrupamientos de unidades que se convierten en nuevas unidades compuestas —por ejemplo, 10 unidades se transforman en una decena la cual se suma con las cifras de las decenas—; se apoyan, en cambio, en la descomposición de números, en un conocimiento de la serie numérica oral, de la suma mental de dígitos y de números redondos (números que terminan en ceros como 10, 20, 30, 100, 2000…).

Es necesario advertir, sin embargo, que propiciar en clase la evolución del cálculo mental reflexivo no es una tarea sencilla. Es necesario disponer de una progresión didáctica que permita fijar metas intermedias, y de un repertorio amplio de procedimientos posibles para poder identificar los que usan los alumnos, para difundirlos, o proponerlos como alternativas a todo el grupo (Caballero, 2018). Por otra parte, hay que considerar que algunos alumnos, frente a la petición de desarrollar procedimientos diversos adaptados a los números en juego, tienden a aferrarse a los algoritmos, cuando ya los conocen, posiblemente porque les proporcionan “ahorro de pensamiento” (Butlen, 1996, p. 381) o más seguridad. Éstas son otras razones para permitir, a partir de tercer grado, una convivencia de ambos acercamientos, el del cálculo reflexivo y el de los algoritmos usuales.

Los trabajos que cité anteriormente para conocer alternativas didácticas para el aprendizaje de la numeración, ofrecen también un repertorio de actividades para el aprendizaje del cálculo reflexivo, particularmente de la suma y la resta. Añadiré que en esta época en que las calculadoras pueden hacer el trabajo de operar con números grandes en poco tiempo, la importancia del cálculo reflexivo, por contraste con el convencional, como un medio de hacer estimaciones rápidas y de controlar errores posibles al teclear en la calculadora, se acrecienta.

Comentario final

¿Entonces, la propuesta es ya no enseñar ni los principios de base y posición del sistema de numeración ni los algoritmos usuales por columnas? No, la propuesta es posponer su enseñanza un par de años en la primaria, cuando los alumnos cuenten ya con mejores condiciones para comprenderlos, e impulsar en los primeros grados un acercamiento a la numeración y a las operaciones aditivas que parta de los conocimientos previos de los niños sobre las numeraciones oral y escrita, y que no dependa de un conocimiento explícito de las propiedades del sdn, en particular, del valor posicional de las cifras. En México es posible observar una tendencia, incipiente, a partir de la reforma de los años noventa en la dirección señalada: en los años setenta se proponía, para primer grado, enseñar los principios de base y posición antes de enseñar el número 10; en los años noventa se sugería enseñar la numeración al menos hasta el 15, como símbolos arbitrarios, y sólo después estudiar el valor posicional de las cifras. También puede observarse un espacio para el desarrollo de procedimientos alternos, del tipo de los que hemos ilustrado como “cálculo reflexivo”. Lo que propongo es intensificar estas tendencias.

Es necesario subrayar, sin embargo, que llevar al aula un trabajo de construcción de la numeración escrita y de cálculo reflexivo como el que hemos esbozado no es sencillo, requiere de la concurrencia de varios factores: enriquecer las secuencias de actividades didácticas disponibles en los libros de texto y en los materiales para la enseñanza, apuntalar estos temas en la formación y actualización de los docentes, multiplicar los proyectos colaborativos con apoyo de docentes expertos y/o de investigadores para que los maestros que se interesen puedan desarrollar la experiencia necesaria. Con respecto a este último factor, es importante insistir en que la gestión de una clase con el enfoque didáctico que hemos descrito aquí para el aprendizaje de la numeración escrita dista mucho de las prácticas usuales, pues ya no se trata de enseñar paso a paso los principios del sdn para escribir los números, sino de, a partir de lo que los alumnos saben, propiciar que escriban los números, que reflexionen sobre su escritura, que identifiquen regularidades, que vean las contradicciones. Ello constituye una tarea compleja, sobre todo porque no abundan ejemplos que puedan tomarse como referencia —es muy probable, por ejemplo, que a los docentes no se les haya enseñado de esa manera—. Lo mismo ocurre con la gestión de clases que buscan dar lugar al cálculo reflexivo, la cual también guarda diferencias importantes con la enseñanza de los algoritmos: no hay “una sola manera de proceder”, sino un conjunto de estrategias que se usan de manera flexible, que varían de una cuenta a la otra y de un sujeto a otro, y cuyo desarrollo depende también en buena medida de la habilidad docente para proponer cálculos que favorezcan distintas estrategias, para identificar procedimientos interesantes y someterlos al grupo, para aportar mejoras oportunas, entre otras cosas. En este sentido, resulta expresivo el siguiente comentario tomado de un estudio sobre una experiencia de cálculo reflexivo llevada a cabo en un grupo de segundo grado:

Los alumnos difícilmente comprendían estas explicaciones (sobre cómo descomponer números para facilitar los cálculos): las seguían, respondían puntualmente a las preguntas que la maestra iba haciendo, pero éstas no les servían a la hora de calcular. Como vimos, más bien los alumnos tendieron a identificar la expectativa de “descomponer números” y se dieron a la tarea de hacerlo, separadamente del propósito de facilitar los cálculos. […] Las puestas en común constituyeron para la docente otro reto mayúsculo, lo cual puso en evidencia la complejidad de la gestión de ese momento: le implicaba identificar procedimientos durante la resolución (ya dijimos que éstos no se explicitaban fácilmente), discernir los que valía la pena hacer públicos, ayudar a los alumnos a explicitarlos, hacer participar a los alumnos en la puesta a prueba de los procedimientos que parecieran interesantes, para ayudarlos a apropiarse de ellos. ¿Cómo se aprende todo esto? (Caballero, 2018, pp. 175-176).

Considerando la complejidad de un proyecto así, aunada a la fuerte tradición de enseñar estos algoritmos en los primeros grados, es claro que el propósito de cambiar la forma de enseñanza de la numeración y de las operaciones no podría realizarse en poco tiempo con un simple cambio de indicaciones curriculares, como varias experiencias nos lo han mostrado (Block, et al., 2007; Ávila, 2004; Block, 2018).

Por ello considero que lo más adecuado es fortalecer las condiciones que mencioné antes, sobre todo el desarrollo de materiales de apoyo, y la formación y la actualización docente, para que las alternativas didácticas al estudio de la numeración y de las operaciones aditivas ganen terreno en la escuela.

---

Bibliografía